Анализ научной публикации А.А. Прокофьева и В.В. Бардушкина «О различных подходах к вычислению площадей сечений»
Шаг 1. Анализ заголовка статьи.
Какой главный результат предполагали авторы?
Главным результатом авторы А.А. Прокофьев и В.В. Бардушкин предполагают обобщить и систематизировать сведения о том, как можно наиболее эффективно решать задачи на тему «Вычисление площадей сечений многогранников».
Список вопросов, на которые хотелось бы получить ответ при прочтении статьи:
Какие существуют методы вычисления площадей сечения?
Какими основными характеристиками различаются подходы вычисления площадей сечения?
Шаг 2. Вопросы из анализа статьи.
Какие причины обусловливают сложность решения задач, в которых требуется найти площадь сечения?
Какие основные определения используются при построении сечений?
Какие основные определения используются при построении сечений?
Какие утверждения (факты) используются при построении сечений?
Какие основные характеристики поэтапно-вычислительного метода?
Какие основные характеристики метода применения теоремы о площади ортогональной проекции многоугольника?
Какие основные характеристики координатно-векторного метода?
Шаг 3. Записать ответы на поставленные вопросы.
Какие причины обусловливают сложность решения задач, в которых требуется найти площадь сечения?
Ответ: Причины:
Необходимость чёткого, обоснованного построения многоугольника, являющегося сечением призмы или пирамиды.
Вычислительные ошибки.
Какие основные определения используются при построении сечений?
Ответ:
Следом плоскости α на плоскости β называют прямую, по которой плоскости α и β пересекаются.
Секущей плоскости на грани многогранника - это отрезок, все точки которого являются общими точками секущей плоскости и грани.
Следом прямой l на плоскости α называют точку, в которой прямая l пересекает плоскость α.
След секущей плоскости на ребро многогранника - это общая точка секущей плоскости и ребра.
Построить сечение многогранника плоскостью означает построить многогранник, все ребра которого – следы секущей плоскости на гранях многогранника, а его вершины – следы секущей плоскости на ребрах многогранника.
Какие основные утверждения (факты) используются при построении сечений?
Ответ:
О плоскости, проходящей через прямую параллельную другой плоскости.
О параллельности следов секущей плоскости.
О пересечении параллельных плоскостей третьей плоскостью.
Какие существуют методы вычисления площадей сечения?
Ответ: Виды методов:
Поэтапно-вычислительный метод.
Применение теоремы о площади ортогональной проекции многоугольника.
Координатно-векторный метод.
Какие основные характеристики поэтапно-вычислительного метода?
Ответ: Как правило в предлагаемых задачах построение заданного сечения многогранника не вызывает трудности у учащихся и представляет собой «простой» многоугольник (треугольник, равнобедренную трапецию и т.д.). В таких случаях, как правило, предпочтительным является подход, связанный с нахождением основных элементов таких многоугольников (сторон, углов), позволяющий по известным формулам планиметрии вычислять их площади.
Какие основные характеристики метода применения теоремы о площади ортогональной проекции многоугольника?
Ответ; Определение. Ортогональной проекцией фигуры на данную плоскость называют множество точек пересечений с этой плоскостью перпендикулярных к ней прямых, проходящих через все точки этой фигуры.
Теорема. Если фигура Ф с площадью Sф лежит в плоскости α, а фигура Ф1 c площадью Sф1 является ортогональной проекцией фигуры Ф на плоскость β, имеет место равенство Sф1= Sф∙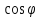 , где 𝜑 – угол между плоскостями α и β.
, где 𝜑 – угол между плоскостями α и β.
Данный подход используется в ситуациях, когда нахождение площади Sпр ортогональной проекции многоугольника, полученного в сечении, и угол 𝜑 между секущей плоскостью и плоскостью проектирования сопряжено с меньшими трудностями, чем непосредственное вычисление площади сечения.
Какие основные характеристики координатно-векторного метода?
Ответ; Координатно-векторный метод удобно применять в случаях, когда полученный в сечении многогранник является четырёхугольником (или треугольником).
Шаг 4. Составить связанный текст, на основе проведенного анализа.
Проанализировав публикацию А. Прокофьева и В. Бардушкина « О различных подходах к вычислению площадей сечений» в разделе «КОНСУЛЬТАЦИЯ» журнала «Математика в школе»., можно сделать вывод, что лавным результатом авторы предполагают обобщить и систематизировать сведения о том, как можно наиболее эффективно решать задачи на тему «Вычисление площадей сечений многогранников».
В статье выделены причины, по которым возникают сложности при решении задач, в которых требуется найти площадь сечения:
Необходимость чёткого, обоснованного построения многоугольника, являющегося сечением призмы или пирамиды.
Вычислительные ошибки.
В публикации выделены основные определения, используемы в теме «Вычисление площади сечения»:
Следом плоскости α на плоскости β .
Секущей плоскости на грани многогранника.
Следом прямой l на плоскости α .
След секущей плоскости на ребро многогранника.
Выделены основные утверждения (факты), используемы в теме «Вычисление площади сечения»:
О плоскости, проходящей через прямую параллельную другой плоскости.
О параллельности следов секущей плоскости.
О пересечении параллельных плоскостей третьей плоскостью.
В публикации выделены методы, используемые при решении задач на вычисление площади сечения:
Поэтапно-вычислительный метод.
Применение теоремы о площади ортогональной проекции многоугольника.
Координатно-векторный метод.
Комбинированный.
Авторами подробно описаны ключевые составляющие каждого из предложенных методов:
Поэтапно-вычислительный метод.
Как правило в предлагаемых задачах построение заданного сечения многогранника не вызывает трудности у учащихся и представляет собой «простой» многоугольник (треугольник, равнобедренную трапецию и т.д.). В таких случаях, как правило, предпочтительным является подход, связанный с нахождением основных элементов таких многоугольников (сторон, углов), позволяющий по известным формулам планиметрии вычислять их площади.
Применение теоремы о площади ортогональной проекции многоугольника.
Данный подход используется в ситуациях, когда нахождение площади Sф1= Sф∙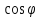 , где 𝜑 – угол между плоскостями α и β.ортогональной проекции многоугольника, полученного в сечении, и угол 𝜑 между секущей плоскостью и плоскостью проектирования сопряжено с меньшими трудностями, чем непосредственное вычисление площади сечения.
, где 𝜑 – угол между плоскостями α и β.ортогональной проекции многоугольника, полученного в сечении, и угол 𝜑 между секущей плоскостью и плоскостью проектирования сопряжено с меньшими трудностями, чем непосредственное вычисление площади сечения.
Координатно-векторный метод.
Координатно-векторный метод удобно применять в случаях, когда полученный в сечении многогранник является четырёхугольником (или треугольником).
Особо следует подчеркнуть, что в статье разобраны примеры задач на нахождение площади сечения, ранее используемых реальных вариантов ЕГЭ.
Практическая значимость данной статьи заключается в том, чтобы помочь учителю при подготовке к урокам по данной теме. Но также, помочь ученикам в самостоятельной подготовке для успешного прохождения итоговой аттестации.







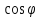 , где 𝜑 – угол между плоскостями α и β.
, где 𝜑 – угол между плоскостями α и β.









