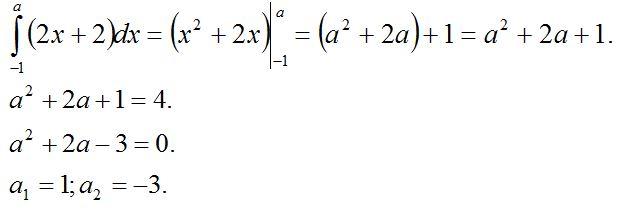Просмотр содержимого документа
«Анықталған интеграл және оның қасиеттері»
Анықталған интеграл және оның қасиеттері
F(b) - F(a) айырмасын y=f(x) функциясының [a;b] кесіндісіндегі анықталған интегралы деп атайды.
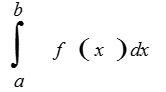
Мұндағы a және b сандары интегралдау шектері: a – төменгі шегі, ал b – жоғарғы шегі.
Анықталған интегралдың негiзгi қасиеттерi.
Берiлген анықталған интегралдың бар болу шарты орындалады деп есептейiк.
10. Тұрақты санды анықталған интеграл белгiсiнiң алдына шығаруға болады:
 ,
,
мұнда k=const .
20. Бiрнеше функциялар қосындысының анықталған интегралы қосылғыштарының анықталған интегралдарының қосындысына тең:
 .
.
Осы екi қасиет интегралдың сызықтық қасиетi деп аталады.
30. Егер [a;b] аралығын [a;c] және [c;b] аралықтарына бөлсек, онда

40. Егер интегралдың жоғарғы шегi мен төменгi шегiнiң орындарын ауыстырсақ, онда оның таңбасы өзгередi:

50. Жоғарғы шегi мен төменгi шегi тең болатын интеграл 0-ге тең
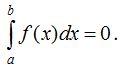
60. Егер [a;b] аралығындағы х айнымалысының барлық мәндерi үшiн  болса, онда
болса, онда
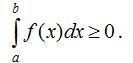
70. Егер [a;b] аралығындағы х айнымалысының барлық мәндерi үшiн  болса, онда
болса, онда
 .
.
80. Егер [a;b] аралығында функциясының ең үлкен және ең кiшi мәндерi сәйкес М және m сандары болса, онда
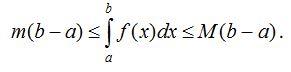
2. Ньютон-Лейбниц формуласы.
Ньютон Исаак (1643-1727) - ағылшын астрономы, физигі, әрі математигі. ХVII ғасырда дифференциалдық және интегралдық есептеулерді математикалық практикаға енгізді.

Туындыны дифференциалдау деп атаған және интеграл белгісін енгізген Лейбниц
Готфрид Вильгельм Лейбниц (1646-1716 жж.) – XVII ғасырдағы неміс рухы туғызған терең де жан-жақты дамыған философ. Екінші жағынан, ол - математик, физик, саясаткер, тарихшы, құқықтанушы.
Теорема. Егер F(X) функциясы [a;b] аралығына f(x) функциясының алғашқы функциясының бiрi болса, онда
 (5)
(5)
Бұл теңдiк Ньютон-Лейбниц формуласы деп аталады.
Анықталған интегралдарға байланысты мысалдар келтіру.
1-есеп.  .
.
Интеграл астындағы функцияның алғашқы функциясын бөлiктеп интегралдау әдiсiмен тауып және оған Ньютон-Лейбниц формуласын қолдансақ,
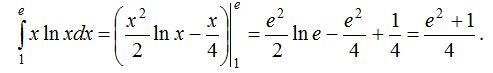
2-есеп.  .
.
Бөліктеп интегралдау формуласы бойынша  болса, онда
болса, онда

3-есеп.
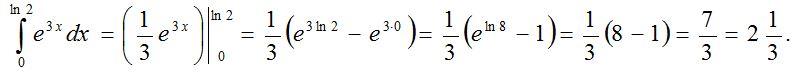
4-есеп.
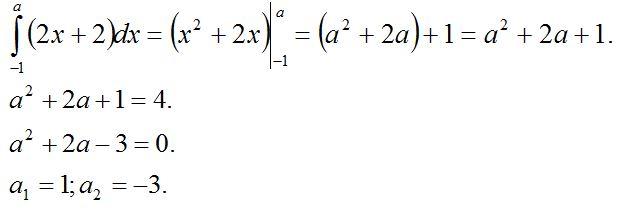






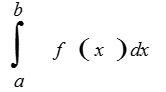
 ,
, .
.

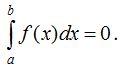
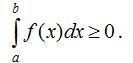
 .
.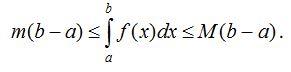

 (5)
(5) .
.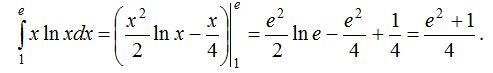
 .
. болса, онда
болса, онда