
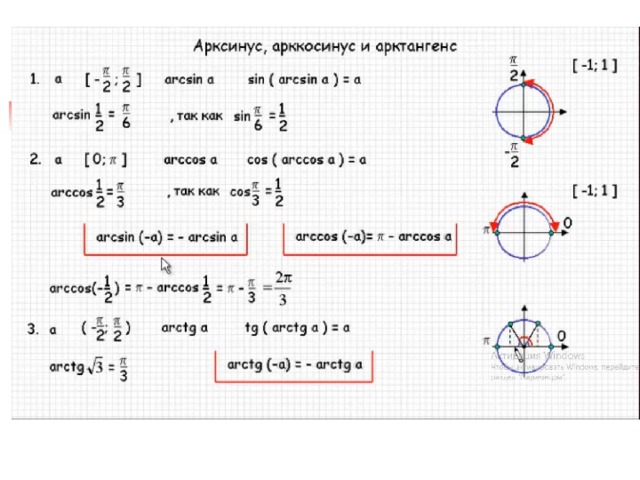
Арксинус, арккосинус, арктангенс жана арккотангенс
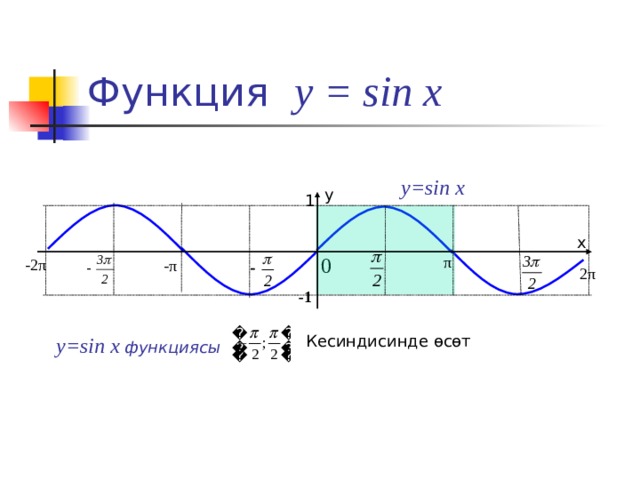
Функция у = sin x
y=sin x
у
1
х
0
π
-2π
-π
2π
-1
Кесиндисинде өсөт
y=sin x функциясы

Арксинус
у
y=sin x функциясы
y=sin x
1
Кесиндисинде өсөт жана
а
болгон ар кандай а саны үчүн
b
b
х
аралыгында
0
b
sin x = a теңдемесинин бир гана b
тамыры болот. Бул b санын a санынын
арксинусу деп атайбыз
а
b=arcsin a
а
-1
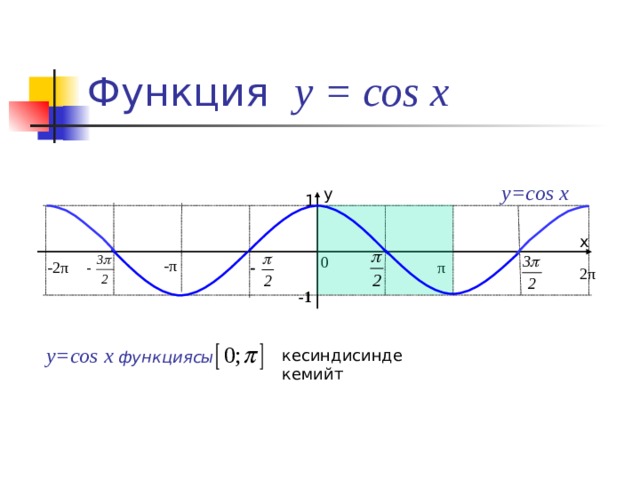
Функция у = cos x
y=cos x
у
1
х
0
-π
-2π
π
2π
-1
y=cos x функциясы
кесиндисинде кемийт
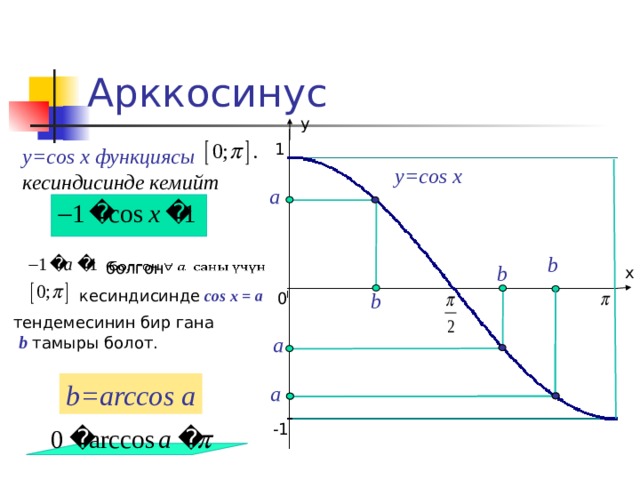
Арккосинус
у
1
y=cos x функциясы
кесиндисинде кемийт
y=cos x
а
b
болгон
b
х
кесиндисинде cos x = a
b
0
тендемесинин бир гана
b тамыры болот.
а
b=arccos a
а
-1
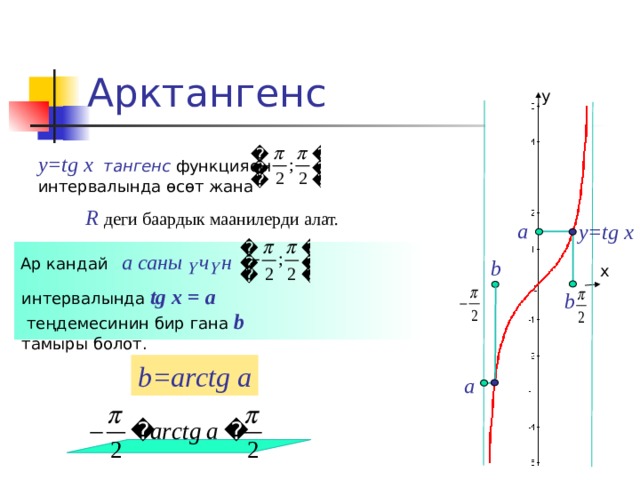
Арктангенс
у
y=tg x тангенс функциясы
интервалында өсөт жана
R деги баардык маанилерди алат.
а
y=tg x
Ар кандай а саны үчүн
b
х
интервалында tg x = a
теңдемесинин бир гана b тамыры болот.
b
b=arctg a
а

Арккотангенс
y
y=ctg x
y=ctg x ф ункциясы
интервалында кемийт
а
жана R деги баардык маанилерди алат
b
x
Ар кандай а саны үчүн
b
интервалында ctg x = a теңдемесинин бир гана b тамыры болот
а
b=arcctg a

№ 116 а.
Ар бир теңдеменин көрсөтүлгөн аралыкта канчадан тамыры бар?
Функциянын графиги бүткул сан огунда өсөт. Демек, теңдеме бул аралыкта бир тамырга ээ болот.

№ 118 а.
Бирдик айланада үүчү t нын маанисин берилген барабардыкты канаатандаргандай кылып t нын көрсөтүлгөн аралыкта жаткан маанисин тапкыла.
Ордината огуна
, демек
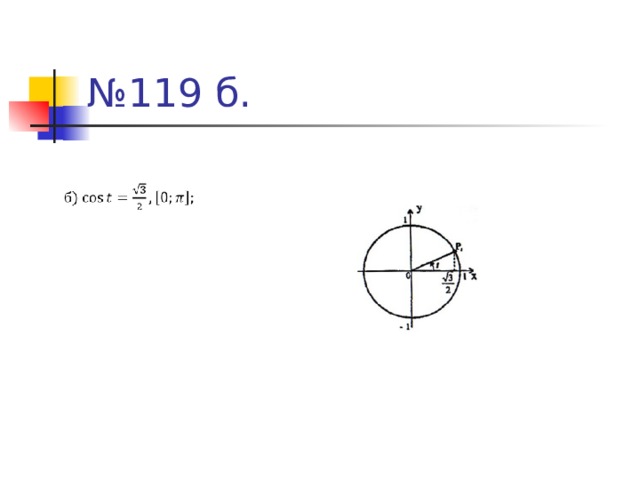
№ 119 б.

№ 122 а.
а) =
№ 124 оозеки

№ 126. туюнтмалардын маанилерин тапкыла

№ 127

№ 128

№ 129. Салыштыргыла

Үй иши
№ 116 в.
№ 118 в
№ 119 а
№ 120 а
№ 121-123 в
№ 125
№ 126-128 а
№ 129 в

№ 127а










































