

Теория:
Что такое синус угла х ? Это отношение противолежащего катета к гипотенузе: sinx = а/с
Что такое косинус угла х ? Это отношение прилежащего катета к гипотенузе: сosx= в/с
Что такое тангенс угла х ? Это отношение противолежащего катета к прилежащему: tgx = а/в
Что такое котангенс угла х ? Это отношение прилежащего катета к противолежащему: ctgx = в/а
Отношения сторон никак не зависят от их длин (при одном угле х), но резко зависят от этого самого угла! И только от него. Поэтому термины
синус, косинус, тангенс и котангенс
относятся к углу.
Угол здесь - главный.

Основные тригонометрическое тождества
Вспомогательные тождества

Практическая часть
1. Вычислить значение tgА, если ctgА = 0,4.
2. β - угол в прямоугольном треугольнике. Найти значение tgβ, если sinβ = 12/13.
3. Определить синус острого угла х, если tgх = 4/3.
4. Найти значение выражения:
6sin 2 5° - 3 + 6cos 2 5°
5. Найти значение выражения:
(1-cosx)(1+cosx), если sinх = 0,3
Ответы (через точку с запятой, в беспорядке):
0,09; 3; 0,8; 2,4; 2,5

6. Найти значение tgβ, если sinβ = 12/13, а
7. Определить sinх, если tgх = 4/3, а х принадлежит интервалу (- 540°; - 450°). 8. Найти значение выражения sinβ·cosβ,
если ctgβ = 1.

Арксинус, arcsin
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ).
Он имеет область определения
– 1 ≤ x ≤ 1 и множество значений
– π/2 ≤ y ≤ π/2. sin(arcsin x) = x
arcsin(sin x) = x
Арксинус иногда обозначают так:
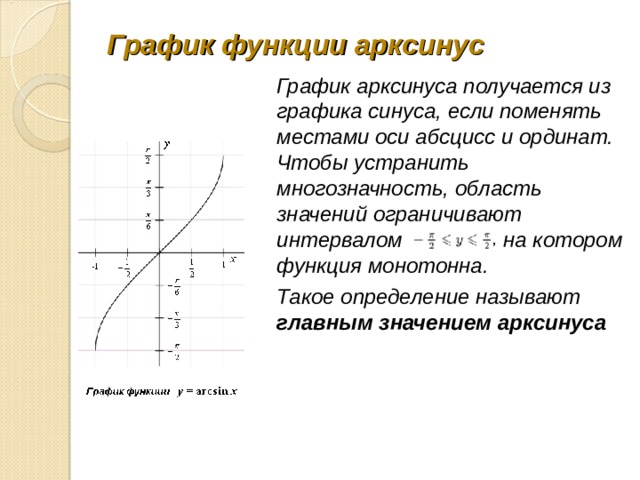
График функции арксинус
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом на котором функция монотонна.
Такое определение называют главным значением арксинуса

Арккосинус, arccos
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения –1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π. cos(arccos x) = x
arccos(cos x) = x
Арккосинус иногда обозначают так:
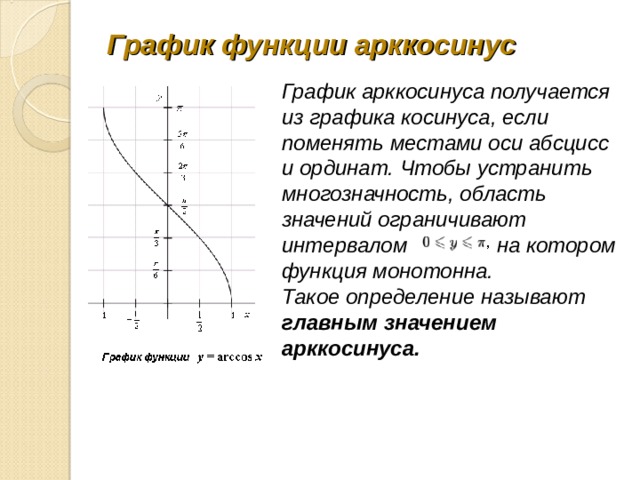
График функции арккосинус
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом на котором функция монотонна. Такое определение называют главным значением арккосинуса.

Четность
Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin x
Функция арккосинус не является четной или нечетной:
arccos(–x) = arccos(–cos arccos x) = arccos(cos( π– arccos x)) = π – arccos x ≠ ± arccos x

Основные свойства арксинуса и арккосинуса

Таблица арксинусов и арккосинусов
В данной таблице представлены значения
арксинусов и арккосинусов, в градусах и
радианах, при некоторых значениях
аргумента.

Формулы

Формулы суммы и разности
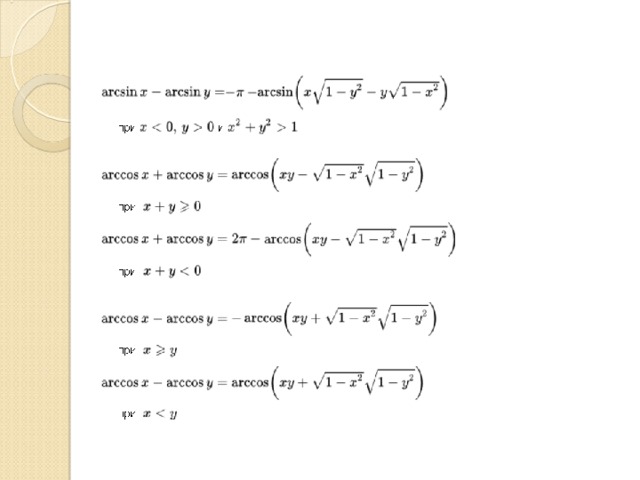
 1 б) arcsin (- пи/2) нет, I - π/2 I1 в) arcsin( - пи/3) нет, I - π/3 I1 г) arcsin( -3/4) да, I -3/4 Iд) arcsin √ (5/2 ) нет, I√ (5/2) I1 и) arcsin( -√( 17/2) нет, I -√ (17/2 ) I1 " width="640"
1 б) arcsin (- пи/2) нет, I - π/2 I1 в) arcsin( - пи/3) нет, I - π/3 I1 г) arcsin( -3/4) да, I -3/4 Iд) arcsin √ (5/2 ) нет, I√ (5/2) I1 и) arcsin( -√( 17/2) нет, I -√ (17/2 ) I1 " width="640"
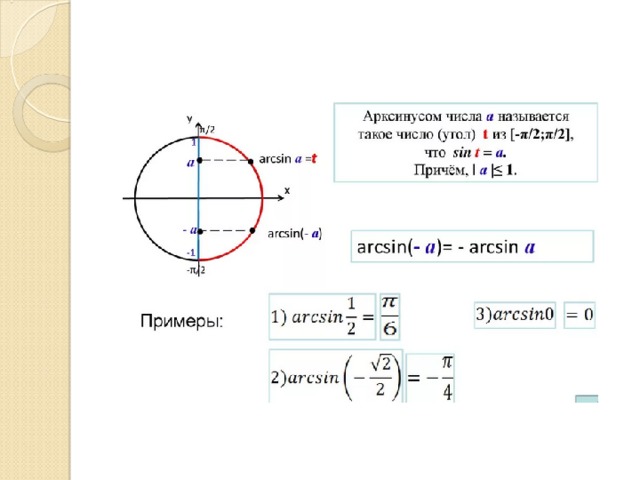
Практическое применение
Имеет ли смысл запись:
а)arcsin пи; б)arcsin -пи/2 в)arcsin -пи/3 г)arcsin -3/4 д)arcsin квадратный корень из 5/2 и)arcsin -квадратный корень из 17/2
Ответы:
а) arcsin( пи); нет, π1
б) arcsin (- пи/2) нет, I - π/2 I1
в) arcsin( - пи/3) нет, I - π/3 I1
г) arcsin( -3/4) да, I -3/4 I
д) arcsin √ (5/2 ) нет, I√ (5/2) I1
и) arcsin( -√( 17/2) нет, I -√ (17/2 ) I1

Имеет ли смысл выражение:
a) arccos π; в) arccos (—√3); б) arcsin (3 - √20); Ответы:

Вычислить






















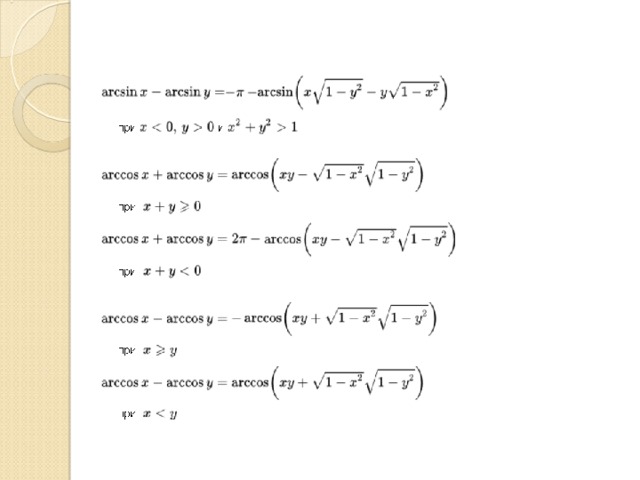
 1 б) arcsin (- пи/2) нет, I - π/2 I1 в) arcsin( - пи/3) нет, I - π/3 I1 г) arcsin( -3/4) да, I -3/4 Iд) arcsin √ (5/2 ) нет, I√ (5/2) I1 и) arcsin( -√( 17/2) нет, I -√ (17/2 ) I1 " width="640"
1 б) arcsin (- пи/2) нет, I - π/2 I1 в) arcsin( - пи/3) нет, I - π/3 I1 г) arcsin( -3/4) да, I -3/4 Iд) arcsin √ (5/2 ) нет, I√ (5/2) I1 и) arcsin( -√( 17/2) нет, I -√ (17/2 ) I1 " width="640"























