Авторская программа "От развлечения к знаниям"(часть 2)

48

УПРАВЛЕНИЕ ОБРАЗОВАНИЯ

АДМИНИСТРАЦИИ ГОРОДА КИСЕЛЁВСКА

МУНИЦИПАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ДОПОЛНИТЕЛЬНОГО ОБРАЗОВАНИЯ ДЕТЕЙ

«СТАНЦИЯ ЮНЫХ ТЕХНИКОВ»

«От развлеченья к знаниям»

образовательная программа

для обучающихся 5-9 классов

срок реализации 3 года

Автор – составитель:

Савицкая Ольга Ивановна

педагог дополнительного

образования

Рассмотрена

На методическом совете

______________________

Утверждена

на педагогическом совете

протокол № 1

от _____________________

Директор МОУ ДОД «СЮТ»:

А.Г.Матвеева_______________

Киселёвск

Пояснительная записка.

Образовательная программа имеет научно – техническую направленность. Программа «От развлечения к знаниям» является модифицированной, так как разработана на основе специальной и методической литературы по математике с учётом рекомендаций, предложенных «Министерством просвещения РСФСР» в сборнике «Программы для внешкольных учреждений – М.:Просвещение,88г», в соответствии с требования к содержанию образовательных программ дополнительного образования детей, утверждёнными на заседании Научно-методического совета по дополнительному образованию детей Минобразования России 03.06.2003 г., примерными требованиями к программам дополнительного образования детей Минобрнауки России (Департамент молодёжной политики, воспитания и социальной защиты детей от 11.12.2006 г.).

Данная образовательная программа отвечает запросам современного общества, так как способствует повышению уровня математического развития, углублению и закреплению теоретических знаний и развитию практических умений по освоению учебного материала, обеспечивает эмоциональное благополучие ребёнка, развивает мотивацию личности ребёнка к познанию и творчеству.

В школе каждый ученик должен хорошо усваивать всё то, что излагает учитель на уроках математики, тщательно выполнять все задания. Но для того чтобы в дальнейшем можно было бы овладеть специальностью, так или иначе связанной с математикой её методами, её применениями, этого недостаточно. Необходимы: самостоятельная творческая работа и сознательное отношение к изучению этого трудного предмета.

Программа ориентирует педагога на формирование прочных знаний, через творческое отношение к уже имеющимся знаниям, применение их в новых, в какой-то мере оригинальных ситуациях.

При изучении программы используется научно - исследовательской ориентации, предусматривающая развитие сообразительности и наблюдательности, умения самостоятельно осуществлять небольшие исследования. Одним из важнейших средств интенсификации обучения математике является эффективная организация и управление поисковой деятельностью школьников в процессе решения различных математических задач и упражнений.

Цель программы: Формирование математических знаний, умений и навыков, способствующих развитию у обучающихся способности к самостоятельному поиску методов решения проблем и творчеству.

Основные задачи:

• Углубить, обогатить, систематизировать и закрепить имеющиеся теоретические знания по математике.

• Формировать практические умения и навыки в решении задач, уравнений и неравенств.

• Развивать логическое, математическое мышление обучающихся, умение рассуждать и доказывать свою точку зрения.

• Воспитывать у обучающихся познавательную активность, способность к самостоятельному поиску методов решения проблем и творчеству.

• Изучить методы и этапы решения задач различных типов, некоторые вопросы комбинаторики, вероятности и моделирования.

• Формировать математически грамотную речь.

При выполнении программы предусмотрено использование различных форм работы с учащимися:

• индивидуальные (карточки, устные ответы),

• групповые (работа в парах сменного состава),

• коллективные (сотрудничество, взаимопомощь, контроль),

• семинары,

• зачёты,

• диспуты,

• формы проблемного обучения (проблемное изложение, частично-поисковая деятельность, исследовательская деятельность),

• соревнование, игра, викторина.

Чтобы придать предмету привлекательность и поднять к нему интерес, в программе используются разнообразные средства: задачи с необычными сюжетами, подстрекающими любопытство, занимательными экскурсиями в область истории математики, неожиданными применениями математики к

практической жизни. Более трудные темы перемежаются с весёлыми историями, афоризмами, головоломками, математическими фокусами и играми. Игры на отгадывание развивают творческие способности человека, его логическое мышление, учат ставить важные вопросы и находить на них ответы. Интеллектуальные игры развивают способности, необходимые для решения инженерных задач, проблем управления и экономики. Материал в программе подобран не только из разделов элементарной математики, в курсе имеются темы, посвященные некоторым разделам высшей математики (аналитической геометрии, топологии, вариационному исчислению, теории вероятности). В программе используются словесные игры, расширяющие эрудицию, развивающие культуру речи и кругозор, учащие работать со словарями. Немалое значение они имеют и для развития мышления и речи. Такие игры дают возможность не только потренировать память, но так же проникнуть в тонкости языка, разобраться в структуре словообразования. От играющих, помимо эрудиции и большого запаса слов, требуются комбинаторные навыки – ведь приходится производить немалый перебор букв и слов. По статистике в словесных играх между «физиками и лириками» чаще побеждают физики.

Благодаря применению различных видов задач, головоломок, игр, содержание программы связано с такими предметами, как физика, история, русский язык, биология, черчение.

Особое внимание обращено на развитие логического мышления и математически грамотной речи, а также интереса к предмету. Обучающиеся приучаются охотно и сознательно мыслить. Для успешного освоения применяются на локальном уровне технология разноуровневого обучения, теория критического мышления, метод обратных задач, взаимоконтроль, технология Коноп (контрольный опрос учащихся с включением игровых моментов), технология развивающего обучения, технология рисования в круге.

Возраст детей, участвующих в реализации данной образовательной программы – 11-16 лет. Набор обучащихся в творческое объединение происходит без предъявления к требованиям к знаниям, умениям и навыкам.

Программа рассчитана на три года обучения.

На первом году обучения объём программы составляет 144 часа при режиме занятий – 2 раза в неделю по 2 часа; на втором и третьем годах составляет также по 144 часа в год при режиме – 2 раза в неделю по 2 часа.

Наполняемость группы на первом году обучения – 15 человек, на втором – 10-12, на третьем – не менее 10 человек.

Обучающийся по окончанию 1 года

знает:

• историю возникновения математических символов, законов и действий;

• схемы построения математических высказываний;

• подходы, приёмы и методы математических рассуждений;

• приёмы вычислений;

• свойства множеств и действия над ними; стратегии выигрыша в игровых ситуациях;

• правила математических игр.

умеет:

• выполнять действия в двоичной системе;

• составлять задания по предложенному ответу;

• выделять существенные признаки математических понятий;

• выполнять действия над множествами;

• самостоятельно осуществлять небольшие исследования;

• рассуждать по несложным вопросам.

Обучающийся по окончанию 2 года

знает:

• линейную, квадратичную, обратно-пропорциональную функции, их свойства, способы задания и методы построения графиков;

• способы решения уравнений, неравенств и их систем;

• виды геометрических преобразований фигур на плоскости;

• виды и свойства фигур на плоскости;

• способы разгадывания ребусов и шифровок.

умеет:

• распознавать и решать различные виды задач,

• выполнять преобразования выражений,

• строить и преобразовывать графики,

• выполнять построения и изменение фигур на плоскости,

• решать уравнения неравенства и их системы с одним неизвестным;

• разгадывать ребусы и шифровки.

Обучающийся по окончанию 3 года

знает:

• способы построения и измерения фигур при отсутствии некоторых чертёжных инструментов;

• способы решения иррациональных уравнений и неравенств, систем уравнений и неравенств с двумя неизвестными;

• виды пространственных геометрических фигур, способы построения их развёрток;

• основы комбинаторики, вероятности и моделирования;

• свойства арифметической и геометрической прогрессии;

• тригонометрические функции, равенства и их свойства;

• методы решения головоломок, софизмов.

умеет:

• решать иррациональные уравнения и неравенства, системы уравнений и неравенств с двумя неизвестными;

• строить дерево размещений и сочетаний;

• моделировать ситуации и измерять вероятность;

• строить развёртки объёмных фигур;

• производить геометрические доказательства;

• решать задачи на геометрическую и арифметическую прогрессии;

• выполнять преобразования тригонометрических выражений.

Ожидаемый результат:

• Повышение познавательного интереса к предмету.

• Умение анализировать условие, определять тип и решать различные задачи.

• Умение строить графики функций, различной сложности, а также, содержащих модули.

• Умение составлять и решать усложнённые типы уравнений, неравенств и их систем с несколькими неизвестными.

• Математически грамотная речь учащихся, умеющих логически правильно доказывать истинность своих высказываний.

• Умение выполнять различные действия с рациональными и иррациональными числами, проводя исследования на максимальные и минимальные значения, делимость.

• Умение выполнять построение и анализировать свойства геометрических фигур.

Эффективность образовательной программы определяется по итогам обучения. Оценка ЗУН проводится по окончанию блока посредством ниже перечисленного инструментария. Результаты освоения содержания программы отслеживается с помощью рубежного и итогового тестирования. В программе предусмотрена система отслеживания и фиксации результатов диагностирования обучающихся.

Диагностический инструментарий:

• входное тестирование исследования логического математического аспекта мышления;

• промежуточные зачёты, анкетирование, тестирование;

• составление тестовых заданий и анализ;

• мониторинг знаний и умений учащихся;

• соревнования и викторины;

• психологические исследования (оценка уровня личностного роста обучающегося).

Успешное усвоение программы возможно при наличии:

• кабинета, с оборудованием (учебная доска, учебная мебель)

• хорошей доски,

• инструментов (циркуль, линейка, треугольник, транспортир),

• настольных игр,

• дидактического материала,

• макетов пространственных геометрических фигур

Учебно – тематический план

1 год обучения

144 часа

№	Наименование раздела	Количество часов
		всего	теория	практика
1	Вводное занятие.	2	1	1
2	Математика как изящное искусство.	4	2	2
3	Мир чисел	26	8	18
4	Задачи из прошлого	4	1	3
5	Числовые множества	20	8	12
6	Математические высказывания и рассуждения	30	11	19
7	Время и его измерение	14	3	11
8	О природе и погоде.	6	2	4
9	Стратегии игр, связанных с шахматами и словами.	22	6	16
10	Повторение	16	2	14
	итого	144	44	100

Содержательная характеристика

1 год обучения

1. Вводное занятие

Знакомство с детьми и их интересами. Экскурсия по учреждению. Знакомство с содержанием программы.

Практическая работа: составление обучающимися индивидуальной образовательной программы, заполнение анкет, игра «Знакомство».

2. Математика как изящное искусство.

Комбинации исходных символических образов, возникающих в мифологии, в результате процесса сложения или умножения. Метод комбинирования объектов применяется в науке. Примеры создания сложных математических форм из простейших, оставаясь на образном уровне мышления. «Божественная пропорция», используемая зодчими; золотое сечение; каноны изображения фигуры человека, цветов.

Практическая работа: применение метода комбинирования на предложенном материале, построение фигур с использованием золотого сечения.

3. Мир чисел

История возникновения чисел, знаков, различных систем счисления. Древние способы вычисления на пальцах; незнакомые признаки делимости, объединяющие или упрощающие уже известные; способы быстрого умножения; особенности цифр 1, 5, 6. Викторина вычислений, без использования карандаша и бумаги.

Практическая работа: тесты, игры и задачи со спичками, выполнение устных вычислений, действий в двоичной системе, определение делимости чисел и их остатков, составление заданий по предложенному ответу, решение числовых головоломок.

4. Задачи из прошлого

Замечательные факты из прошлого о задачах с поэтическими названиями.

Задачи, записанные в стихотворной форме. Историческая культура и образ жизни народов в математических задачах.

Практическая работа: решение задач из прошлого и записанных в необычной форме.

5. Числовые множества

Методика определения существенных признаков математических понятий и методика исключения лишнего. Большие числа, бесконечные множеств и действий над ними. Круги Эйлера, решение Задачи Эйлера.

Практическая работа: решение задач на логическое мышление, ребусов, кросснамберов, построение кругов Эйлера, выполнение методических тестов, выполнение действий над множествами.

6. Математические высказывания и рассуждения.

Математические высказывания. Отрицание, дизъюнкция, конъюнкция. Разделение высказываний на виды: «все», «некоторые» и «отрицание». Подходы, приёмы и методы математических рассуждений. Правила крайнего. Правило расположения элементов высказывания. Теорема Софии Жермен для составных чисел.

Практическая работа: составление таблиц – схем для определения истинности высказываний, игра «Отгадывание чисел», нахождение наибольших и наименьших сумм и произведений.

7. Время и его измерение

История происхождения знаков действий. Истории юлианского, китайского и русского календарей. История появления часов. Григорианская реформа. Семидневная неделя. Летоисчисление. Совпадение числовых стрелок (задача).

Практическая работа: составление вопросов по теме «Время», составление и решение задач на летоисчисление.

8. О природе и погоде.

Математический вечер о природных явлениях. Задачи на темы: «Горение без пламени и жара», «Разнообразие погоды», «Сколько весит весь воздух».

Практическая работа: вопросно-ответная работа, решение задач по данной теме.

9. Стратегии игр, связанных с шахматами и словами

Варианты выигрышных стратегий в различных играх. Изоморфизм или одинаковое строение игр. Количество возможных шахматных партий. Принцип игры в шахматы автомата. Различные виды шахматных досок и правила игры на них. Как шахматы превращаются в сказочные, при изменении правил игры.

Практическая работа: решение заданий, связанных с ходом коня; словесные игры: анаграммы, метафоры, цепочки, шахматные партии.

10. Повторение.

Числовые множества и действия над ними. Нахождение наибольших и наименьших значений при сложении, умножении и других математических действиях. Математические высказывания, определение их истинности или ложности. Подведение итогов.

Практическая работа: тесты по темам: «Мир чисел», «Математические высказывания»; математические, шахматные и словесные игры; головоломки, кроссворды, кросснамберы по пройденным темам; выполнение математических действий над числовыми множествами, решение задач о времени и природе.

Учебно – тематический план

2 год обучения

144 часа

№	Наименование раздела	Количество часов
		всего	теория	практика
1	Входное тестирование.	2	1	1
2	Решение задач.	90	25	65
3	Графики функций	22	7	15
4	Геометрические фигуры на плоскости.	22	10	12
5	Повторение	8	3	5
	Итого	144	46	98

Содержательная характеристика курса

2 год обучения

1. Входное тестирование

Содержание курса на год.

Практическая работа: тестирование на уровень подготовленности.

2. Решение задач

Распознавание вида задач. Занимательные задачи. Задачи на восстановление и преобразование выражений. Задачи на составление уравнений, неравенств и их систем. Задачи на растворы, сплавы и смеси. Задачи на пропорции и проценты. Задачи на доказательство, объяснение и метод математической индукции. Графики движения и задачи на движение. Задачи повышенной трудности.

Практическая работа: решение различных видов задач, построение графиков движения.

3. Графики функций

Области применения системы координат. Понятие функции и способы её задания. Геометрическое преобразование графиков функций. Систематизирование видов функций и их свойств. Графический метод решения систем уравнений и неравенств. Графики функций, содержащих модуль.

Практическая работа: игра «Морской бой», построение рисунков по координатам, построение графиков функций, исследование функций, решение систем уравнений и неравенств.

4. Геометрические фигуры на плоскости

Повторение аксиом планиметрии. Изучение фигур на плоскости и их свойств. Виды теорем и условий. Построение, повороты, симметрия.

Практическая работа: игры со спичками, доказательство теорем, построение и видоизменение геометрических фигур.

5. Повторение

Повторение правил решения задач различных видов, методов расшифровки ребусов, свойств фигур. Подведение итогов.

Практическая работа: викторина задач, ребусы, шифровки, игры со словами, шахматные игры, судоку.

Учебно – тематический план

3 год обучения

144 часа

№	Наименование раздела	Количество часов
		всего	теория	практика
1	Повторение тем с усложнением.	34	13	21
2	Геометрические фигуры в пространстве	20	9	11
3	Комбинаторика, вероятность и моделирование.	48	19	29
4	Прогрессии	8	2	6
5	Тригонометрия.	8	2	6
6	Развиваем логику.	26	3	23
	итого	144	48	96

Содержательная характеристика курса

3 год обучения

1. Повторение тем с усложнением

Систематизация знаний о числовых множествах. Обобщение способов преобразования рациональных выражений и методов разложение на множители. Выход из затруднительных положений при построении и измерении фигур. Усложненные системы уравнений. Исследование и сравнение графиков. Решение рациональных неравенств. Системы неравенств с двумя неизвестными. Появление потерянных и посторонних корней у уравнений. Иррациональные уравнения и неравенства.

Практическая работа: выполнение заданий на построение, исследование и решение уравнений, неравенств и их систем, логическая игра с танграмами

2. Геометрические фигуры в пространстве.

Сравнение свойств фигур в плоскости и пространстве. Геометрические доказательства. Рассмотрение видов многогранников. Комбинации тел

вращения и многогранников.

Практическая работа: построение развёрток объёмных фигур, исследование и доказательство свойств пространственных фигур.

3. Комбинаторика, вероятность и моделирование.

Введение в комбинаторику. Изучение комбинаторных моделей и игр. Дерево размещений и сочетаний. Введение в теорию вероятности. Меры вероятности. Графы к задачам. Изучение секретов шахматного автомата.

Практическая работа: построение графов к задачам, конкурс мудрецов, измерение вероятности, моделирование ситуаций, построение дерева размещений и сочетаний.

4. Прогрессии

История возникновения древнейшей прогрессии. Систематизация знаний и сравнение свойств арифметической и геометрической прогрессий. Применение прогрессия в подсобном хозяйстве.

Практическая работа: решение задач на прогрессии.

5. Тригонометрия

Сравнение свойств и графиков тригонометрических функций. Тригонометрические формулы и тождества.

Практическая работа: применение тригонометрических функций при решении геометрических задач и в жизни, преобразование выражений, содержащих тригонометрические функции.

6. Развиваем логику.

Геометрические софизмы. Алгебраические комедии. Геометрические головоломки и викторины. Математическая расшифровка. Постановка пьесы «Живая геометрия». Подведение итогов.

Практическая работа: решение логических задач, головоломок, ребусов.

Ключевые понятия:

• Абстрагирование – выделение существенных и несущественных признаков понятий.

• Аксиома – утверждение, не требующее доказательства.

• Анаграмма – слово, составленное из всех букв данного слова.

• Геометрия – наука, изучающая фигуры и их свойства; раздел математики.

• Дробь – запись частного чисел в виде числителя, знаменателя и дробной черты.

• Инженер – люди, занимающиеся изучением и разработкой изобретений в разных областях.

• Интернет – это охватывающая земной шар компьютерная сеть, которая даёт людям во всём мире быстрый доступ к информации, знаниям, развлечениям и мнениям людей.

• Квадрат – четырёхугольник, у которого все стороны и углы равны.

• Кросснамбер – кроссворд, заполняемый числами.

• Метаграмма – получение нового слова путём замены одной из букв данного слова на другую.

• Палиндромы – слова, которые читаются одинаково слева направо и справа налево.

• Параллелограмм – четырёхугольник, у которого все стороны параллельны.

• Планиметрия – раздел геометрии, изучающий фигуры и их свойства на плоскости.

• Прямоугольник – четырёхугольник, у которого все углы прямые.

• Стереометрия – раздел геометрии, изучающая фигуры и их свойства в пространстве.

• Судоку – цифровая головоломка, пришедшая к нам из Страны восходящего Солнца. Необходимо заполнить пустые клетки цифрами от 1 до 9 так, чтобы в каждой строке, столбце и квадрате цифры не повторялись.

• Трапеция - четырёхугольник, у которого две стороны параллельны.

• Треугольник – фигура, состоящая из трёх точек попарно соединенных отрезками.

• Тригонометрия – раздел математики, изучает отношения сторон, являющиеся функциями угла.

• Функция – зависимость переменной у от переменной х, при которой каждому значению х соответствует единственное значение у.

Список литературы для педагога и обучающихся:

1. Бобровский, В. П. Арифметические задачи теории делимости [Текст] / В. П. Бобровский, Л. Н. Беляева, Ф. М. Абляева, Н. И. Иванова – Караганда: САНАТ– Полиграфия, 2005. – 76 с.

2. Виленкин, Н. Я. Факультативный курс. Избранные вопросы математики (7-8 кл.) [Текст] / Н. Я. Виленкин, Р. С. Гутер, А. Н. Земляков, И. Л. Никольская; под ред. В. В. Фирсова - М. : Просвещение, 1988. – 192 с.

3. Гик, Е. Я. Занимательные математические игры. [Текст] / Е. Я. Гик – М. : Знание, 1987. – 186 с.

4. Глеман, М. Вероятность в играх и развлечениях: Элементы теории вероятностей в курсе сред. школы. [Текст] Пособие для учителя / М. Глеман, Т. Варга; пер. с фр. А. К. Звонкина – М. : Просвещение, 1989. – 176 с.

5. Зак, В. Отгадать, чтобы найти! [Текст] : научно – популярная литература / В. Г. Зак, Я. Н. Длуголенский. – Л. : Дет. лит., 1988. - 175 с.

6. Игнатьев Е.И. В царстве смекалки [Текст] / Е. И. Игнатьев ; под редакцией М.К.Потапова.- М. : Наука, 1984г. – 178 с.

7. Кузнецова, Л. В. Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы . 9 класс [Текст] / Л. В. Кузнецова, Е. А. Бунимович, Б.П. Пигарев, С. Б. Суворова. – 13 изд.,стереотип. – М. : Дрофа, 2007. – 191 с.

8. Коваль, С. От развлечения к знаниям: математическая смесь [Текст] / С. Коваль; пер. с польского О. Унгурян - Варшава, 1982. – 534 с.

9. Кордемский, Б.А. Математическая смекалка [Текст] / Б.А. Кордемский – М. : Гос. изд–во физико–математической литературы, 1959. – 576 с.

1. Кострикина, Н. П. Задачи повышенной трудности в курсе алгебры 7-9

классов [Текст] : кн. для учителя / Н. П. Кострикина – М. : Просвещение, 1991. – 239 с.

1. Крысин, А. Я Поисковые задачи по математике (4-5 классы) [Текст] : пособие для учителей / А. Я. Крысин, В. Н. Руденко, В. И. Садкова, А. В. Соколова, А. С. Шепетов, Ю. М. Колягин – М. : Просвещение, 1989. – 95 с.

2. Лурье, М. В. Задачи на составление уравнений. [Текст] / М.В. Лурье, Б. И. Александров - М. : Наука, 1986. – 80 с.

3. Нагибин, Ф. Ф. Математическая шкатулка [Текст] : пособие для учащихся 4-8 кл. сред. шк./ Ф. Ф. Нагибин , Е. С. Канин. – 5-е изд. - М. : Просвещение, 1988. – 160 с.

4. Математика в школе [Текст] : научно- теорет. и метод. журн. / зарегестр. Государственным комитетом РФ по печати, рег. № 015437. – 1934, май - . – М. : Школа – Пресс, 2001. - . – 2001, № 3. – 33000 экз.

5. Никольская, И. Л. Факультативный курс по математике [Текст] : учеб. пособие для 7-9 кл. сред. шк. / сост. И. Л. Никольская. – М.: Просвещение, 1991. – 383 с

6. Паламарчук, В. Ф. Школа учит мыслить [Текст] : пособие для учителей – М. : Просвещение, 1989. – 144 с.

7. Перельман, Я. И. Занимательная алгебра. [Текст] / Я. И. Перельман – 13 изд. – М.: Наука, 1985. – 200 с.

8. Петрова, Ф.Г. Математические вечера [Текст] / Ф.Г. Петрова – Ижевск: Удмуртия, 1988. – 184 с.

9. Пономарёв, С. А. Сборник задач по математике для 4-5 классов [Текст] : пособие для учителей / С. А. Пономарёв, П. В. Стратилатов, Н. И. Сырнев. – М. : Просвещение, 1979. – 272 с.

10. Фридман, Л. М. Как научиться решать задачи : беседы о решении мат. задач. [Текст] : пособие для учащихся / Л. М. Фридман, Е. Н. Турецкий, В. Я. Стеценко; Под ред. Л. М. Фридмана. – М. : Просвещение, 1989. – 160 с.

11. Яковлев, Г. Н. Геометрия. Теория и её использование для решения задач [Текст] : учебное пособие / Г. Н. Яковлев - Минск: Альфа, 1994. – 336 с.

Приложение № 1

Дидактический материал к программе

1 год обучения

№	наименование раздела	материал
1	Вводное занятие.	Бланки анкет (А-1)
2	Математика как изящное искусство.	Наглядный материал для комбинирования элементов. Наборы геометрических фигур. Изображение фигуры человека с заданными пропорциями.
3	Мир чисел	входной тест-таблица (т-1). Карточки с заданиями для устного счёта. Числовой субтест Айзенка.(Т-2).
4	Задачи из прошлого	Факты из истории
5	Числовые множества	Тест определения способности к абстраги-рованиюматематических понятий. (Т-3) Методика исключения лишнего. (Т-4)
6	Математические высказывания и рассуждения	Карточки с заданиями по осуществлению исследований. Рубежный диагностический материал.
7	Время и его измерение	Изображение чисел и знаков из истории математики.
8	О природе и погоде.	Задачи по теме.
9	Стратегии игр, связанных с шахматами и словами.	Шашки, шахматы. Примеры анаграмм, палиндромов.
10	Повторение	Ребусы, загадки, кросснамберы, танграмы Математические игры. Итоговый диагностический материал.

Приложение № 2

Дидактический материал к программе

2 год обучения

№	наименование раздела	материал
1	Входное тестирование.	Входной диагностический материал. Анкета для определения потребностей учащихся. (А-2).
2	Решение задач.	Карточки для групповой работы по темам: «Неравенства», «Деление на части прямо и обратно пропорциональные данным», «Проценты». Рубежный диагностический материал.
3	Графики функций	Чертежи графиков функций. Образцы рисунков в системе координат.
4	Геометрические фигуры на плоскости.	Методика исключения лишнего (Т-3) Образцы фигур и чертежи.
5	Повторение	Ребусы, загадки, кросснамберы. Итоговый диагностический материал.

Приложение № 3

Дидактический материал к программе

3 год обучения

№	наименование раздела	материал
1	Повторение тем с усложнением.	Танграмы. Карточки с задачами: «Тремя двойками», «Тремя тройками», «Тремя четвёрками», « Четырьмя единицами», «Четырьмя двойками». Плакат с формулами сокращенного умножения. Изображения графиков функций.
2	Геометрические фигуры в пространстве	Чертежи и макеты многогранников и тел вращения.
3	Комбинаторика, вероятность и моделирование.	Материал для экспериментов по теории вероятности. Набор для игры «С тремя дисками». Карточки с задачами по теме. Доска, шахматы.
4	Прогрессии	Плакат с формулами арифметической и геометрической прогрессий.
5	Тригонометрия.	Тригонометрические формулы. Таблицы Брадиса.
6	Развиваем логику.	Карточки с логическими заданиями. Рисунки в системе координат. Ребусы, загадки, кросснамберы. Итоговый диагностический материал.

Приложение № 4

Рубежный диагностический материал

1 года обучения

1. Числовая головоломка.

▲+▲=▲; □+☼=○;

⌂-2=□; 9-□=◊;

☼+☼=⌂; 2+⌂=8.

☼◊▲▲•⌂⌂▲=?; ◊⌂▲□•□○▲=?; ○⌂○•◊▲□=?.

1. Методика «Числовой ряд».

№1	3	4	5	6	7	8
№2	5	10	15	20	25	30
№3	8	7	6	5	4	3
№4	9	9	7	7	5	5
№5	3	6	9	12	15	18
№6	8	2	6	2	4	2
№7	8	9	12	13	16	17
№8	27	27	23	23	19	19
№9	8	9	12	13	16	17
№10	1	2	4	8	16	32
№11	22	19	17	14	12	9
№12	4	5	7	10	14	19
№13	12	14	13	15	14	16
№14	24	23	21	20	18	17
№15	16	8	4	2	1	1/2
№16	18	14	17	13	16	12
№17	12	13	11	14	10	15
№18	2	5	10	17	26	37
№19	21	18	16	15	12	10
№20	3	6	8	16	18	36

1. Ребус.

ЧТОיּ ОШО יּיּיּСЯ, О Ь

32Ж3 321 12

СЯ.

1243

1. Логические задачи.

1.Профессор ложиться спать в 8 часов вечера, а будильник заводит на 9 часов утра. Сколько будет спать профессор?

2.Может ли мужчина жениться на сестре своей вдовы?

3.Есть ли 7 ноября в Австралии?

4.У Мамеда 10 овец. Все, кроме 9, сдохли. Сколько осталось овец?

5.Вы-пилот самолёта, летящего из Гаваны в Москву с двумя посадками в Алжире. Сколько лет пилоту?

6. Обычно месяц заканчивается 30 или 31 числом. В каком месяце есть 28 число?

7. Ты заходишь в тёмную комнату. У тебя газовая и бензиновая лампы, что зажжешь в первую очередь?

8.Один поезд идет из Москвы в Прагу, а другой из Праги в Москву. Вышли они одновременно, скорость первого в 2 раза больше скорости второго. Какой поезд будет дальше от Москвы в момент их встречи?

9.Отец с сыном попали в катастрофу. Отец скончался. К сыну в палату входит хирург и говорит, показывая на него: «Это мой сын». Может ли такое быть?

10.Палку нужно распилить на 12 частей. Сколько надо сделать распилов?

11.На руках 10 пальцев. Сколько пальцев на 10 руках?

12.Археологи нашли монету, датированную 35 годом до нашей эры. Возможно ли это?

13.В каком количестве взял Ной зверей в свой ковчег?

14.Врач прописал больному три укола через пол часа. Сколько потребуется времени, чтобы сделать все уколы?

15. Сколько цифр «9» в ряде чисел от 1 до 100?

16.Одинокий сторож умер днём. Получит ли он пенсию?

17.Горели 7 свечей. Три погасло. Сколько свечей осталось?

18.Кирпич весит 1 кг плюс ещё пол кирпича. Сколько весит кирпич?

19.Под каким кустом сидит заяц во время дождя?

1. Восстанови +83□4□579

6536□4□

□□2□84□3

1. Рисунок по координатам. (2;-2), (0;3), (-2;-2), (3;1), (-3;1), (2;-2)

2. Найди пересечение множеств и составь из букв слово. А={н,т,р,б,а,к,о,ю,и,ш,п,е}и В={и,э,н,к,з,п,д,о,а,т,р,ж}

Ответы:

1)▲=0 ◊=5 ○=7 ⌂=6 ☼=3 □=4

3500•660=2310000; 5604•470=2633880; 767•504=386568.

2)

9	10
35	40
2	1
3	3
21	24
2	2
20	21
15	15
20	21
64	128
7	4
25	32
15	17
15	14
1/4	1/8
15	11
9	16
50	65
9	6
38	76

3)

1. 1час

2. нет

3. да

4. 9

5. твой возраст

6. во всех

7. спичку

8. одинаково

9. да, это мать

10. 11

11. 50

12. нет

13. по паре

14. 1 час

15. 20

16. нет

17. 3 свечи

18. 2 кг

19. мокрым

4)Ребус

Чтобы хорошо учиться нужно сильно потрудиться.

5)Восстанови

83741579+6536844=90278423

6) Рисунок звезда

7)Слово «тропинка».

Результаты:

1. Числовая головоломка. (5 баллов)

2. Методика «Числовой ряд». (20 баллов)

3. Логические задачи (19 баллов).

4. Ребус.(3 балла)

5. Задание на восстановление. (3 балла)

6. Построение рисунка по координатам.(5 баллов)

7. Задание по теме «Множество». (5 баллов)

Максимально 60 баллов.

Высокий уровень – 51-60 баллов.

Средний уровень – 30-50 баллов.

Низкий уровень – менее 30 баллов.

Приложение № 5

Итоговый диагностический материал

1 года обучения

1. Приведи примеры анаграмм (2 словесные и 2 числовые).

2. Приведи примеры палиндромов (2 словесных и 2 числовых).

3. С помощью цепочки слов из метаграмм перейди за 5 шагов от слова « роза» к слову «волк».

4. Исключи лишнего

№1	8	-4	5	18	20
№2	5	10	15	21	25
№3	8,7	-3	6	5,1	4
№4	делимое	частное	плюс	деление	делитель
№5	3	6	9	22	15
№6	8	2	6	3	4
№ 7	3х²	-4х	3х+8у	4у	18х²
№8	11	27	23	17	19
№9	прямоугольник	треугольник	ромб	квадрат	параллелограмм
№10	12	14	13	15	145
№11	десять	число	дробь	буква	пятнадцать
№12	24	23	21	20	18

1. Реши задачи :

   • Подсчитай, сколько метров бумажной ленты потребуется для утепления трёх окон, состоящих из двух одинаковых створок. Ширина створки 60 см, а высота 1 м 50 см.

   • Бабушке нужно поджарить 6 котлет, а на сковородке помещается только 4 котлеты. Каждую котлету нужно жарить 5 мин на одной стороне и 5 мин на другой. Сколько времени потребуется, чтобы поджарить 6 котлет на этой сковородке?

1. Зная возможные скорости движения, составь и реши задачу.

Скорость пешехода: 4-6 км/ч.

Конь: 12-15 км/ч.

Велосипедист: 12-15 км/ч.

Катер: 70-80 км/ч.

Поезд: 40-80 км/ч.

1. Перечерти фигуры. Подпиши под фигурами их названия.

1. Построй в системе координат фигуру и найди координаты пересечения её диагоналей. (-2;7), (4;7), (4;-1), (-2;-1).

Ответы:

3. роза – коза – поза – пола - полк – волк

4.

-4
10
-3
плюс
22
3
3х+8у
27
треу-гольник
145
буква
23

5.

• 5 м 40 см

• 15 мин

7. квадрат, параллелограмм, трапеция, ромб, треугольник, окружность

8. (1;3)

Результаты:

1. Каждая анаграмма по 1 баллу. (4 балла)

2. Каждый палиндром по 1 баллу. (4 балла)

3. Метаграмма (5 баллов).

4. Исключи лишнего (12 баллов)

5. Каждая задача по 3 балла. (6 баллов)

6. Составление задачи - 2 балла, решение - 3 балла, оригинальность 1 балл. (6 баллов)

7. Построение фигур по 1 баллу, название 2 балла. (18 баллов)

8. Построение фигуры по координатам – 3 балла, проведение диагоналей – 1 балл, нахождение координаты точки – 2 балла. (6 баллов)

Максимально можно набрать 61 балл.

Высокий уровень – 55-61 баллов.

Средний уровень – 30-54 баллов.

Низкий уровень – менее 30 баллов.

Приложение № 6

Входной диагностический материал

2 года обучения

1) Восстанови +53□4□577

2536□4□

□□2□84□3

2) Исключи лишнего

№1	6	-4	13	15	250
№2	225	10	153	2121	257
№3	18,7	-3,98	6,54	5,1	1,4
№4	разность	минус	плюс	вычитаемое	уменьшаемое
№5	5	15	10	22	35
№6	8	2	6	3	4
№ 7	23х²	74х	3х+8у	74у	8х²
№8	7	27	13	5	41
№9	трапеция	треугольник	ромб	квадрат	параллелограмм
№10	12	14	13	15	145
№11	числитель	деление	дробь	буква	пятнадцать
№12	4	23	22	20	28

3) Составь и запиши 2 ребуса.

4) Ответь на вопросы:

1. Какой год в России был самым коротким и почему?

2. В старину на масленицу использовалась линейка. Объясните, зачем?

3. Русский царь Алексей Михайлович на книге, посвящённой соколиной охоте, сделал надпись, которая впоследствии стала известной русской пословицей. Воспроизведите эту надпись. («Делу – время, потехе – час», слово «потеха» означает охота.)

4. В каком календаре 13 месяцев?

5. Сколько дней в сентябре?

6. Назовите дату дня весеннего равноденствия.

7. Какой месяц древние славяне называли лютым?

8.На сколько временных поясов разделён весь земной шар?

1. Бабушка справляла все дни рождения, всего 15 дней рождения. Сколько лет бабушке, в каком году она родилась?

Ответы:

1. 53741577+ 2536846=56278423

-4
10
-3
плюс
22
3
3х+8у
27
треугольник
145
буква
23

4)

1. Самым коротким был 1699 год в связи с переходом на празднование Нового года с 1 января.

2. Линейкой называлась тройка лошадей, и она была незаменимым атрибутом народных гуляний.

3. «Делу – время, потехе – час», слово «потеха» означает охота.

4. Лунно-солнечном

5. 30

6. 21.03

7. Февраль

8. 24

9. 60 лет, 1948 29 февраля

Результаты:

1. Восстанови. (2 балла)

2. Исключи лишнего (12 баллов)

3. Каждая ребус по 3 балла. (6 баллов)

4. Ответы на вопросы (18 баллов)

Максимально можно набрать 38 баллов.

Высокий уровень – 33-38 баллов.

Средний уровень – 18-32 баллов.

Низкий уровень – менее 18 баллов.

Приложение № 7

Рубежный диагностический материал

2 года обучения

1 Решите неравенство, используя метод интервалов:

(х+3)(х-1)(х-10)

2. Задача:

На одно платье и 3 сарафана пошло 9 м ткани, а на 3 таких же платья и 5 таких же сарафанов – 19м ткани. Сколько ткани требуется на одно платье и сколько на один сарафан?

3. Задача:

Объём подсолнечного масла в бутылке составляет 1000мл. Отклонения не более 2 %. Какой наибольший и наименьший объём масла возможен в бутылке.

4. Решите уравнение: х²+6х+8=0

5. Разложите на множители: 3х+ ху²-х²у-3у.

6. Составьте и решите задачу на составление уравнения.

7. Задача:

В сплаве весом 10 кг отношение меди к цинку равно 4 : 1, во втором сплаве весом 16 кг отношение меди к цинку равно 1 : 3. Сколько надо добавить чистой меди к этим сплавам, чтобы получить сплав, в котором отношение меди к цинку равно 2 : 3?

8. В системе равенств цифры зашифрованы буквами. Попробуйте восстановить первоначальный вид системы.

ПРУТ-КАМА=КУРА,

ТУР-РАК=КОМ,

ТИП-РОК=АУТ.

9. Задача:

В классе 27 человек. Каждый мальчик дружит с четырьмя девочками, а каждая девочка – с пятью мальчиками. Сколько в классе мальчиков и сколько девочек?

Ответы:

1. (-ω;-3)Ú(1;10)

2. 3м на платье и 2м на сарафан

3. От 980мл до 1200 мл.

4. -2; -4.

5. (ху-3)(у-х)

7. 9 кг.

8. 7194-3282=3912, 491-123=368, 457-163=294.

9. Пусть а – число мальчиков, с- число девочек. Найдём общее количество дружб двумя способами. Поскольку каждый мальчик дружит с 4 девочками, это число равно 4а. С другой стороны, каждая девочка дружит с 5 мальчиками, значит это число равно 5с. Получаем уравнение 4а=5с. Посколькуа+с=27, то а=15, с=12.Мальчиков 15, девочек 12.

Результаты:

1. Неравенство (2 балла)

2. Задача. (3 балла)

3. Задача. (3 балла)

4. Уравнение (2 балла)

5. Разложите на множители (3 балла)

6. Составление задачи – 3 балла, решение – 3 балла. (6 баллов)

7. Задача. (5 баллов)

8. Задача на восстановление. (5 баллов)

9. Логическая задача. (5 баллов)

Максимально можно набрать 34 балла.

Высокий уровень – 29-34 балла.

Средний уровень – 17-28 баллов.

Низкий уровень – менее 17 баллов.

Приложение № 8

Итоговый диагностический материал

2 года обучения

1. Задача на логику :

В кругу сидят Иванов, Петров, Марков и Карпов. Их имена: Андрей, Сергей, Тимофей, Алексей. Известно, что: 1) Иванов не Алексей и не Андрей; 2) Сергей сидит между Марковым и Тимофеем; 3) Карпов не Сергей и не Алексей; 4) Петров сидит между Карповым и Андреем.

Как зовут Иванова, Петрова, Маркова и Карпова?

1. Задача, решаемая методом подбора:

В магазин привезли 106 л масла в пяти- и семилитровых бидонах. Сколько всего бидонов масла привезли в магазин?

1. Задача на скорость:

Малыш может съесть 600 г варенья за 6 минут, а Карлсон в 2 раза быстрее. За какое время они съедят это варенье вместе?

1. Восстановите запись:

х* 2 * 3

* *

* * * 8 7

* * * * *

2 * 0 0 4 *

5. Задача на логику :

В бочке 28 л бензина. Имеется два ведра емкостью по 7 л, в которые

нужно налить по 6 л бензина. Кроме того, есть черпак ёмкостью 4 л. Как

можно осуществить разлив?

6. Найдите Х из пропорции.

9·(¹º∕75+0,56) ‗ 0,25:(∕6) - ∕25

5Х ³³∕2 - ¹²∕9 .

7. Сократите дробь: а³-9ав² .

а²-3ав

8. Решите систему уравнений:

х+2у=13 и ху=15.

9. Разложите многочлен на множители

а) х²-15х+26

б) 9х²-48х+64.

10. Постройте график функции: у=х²-2х+3.

11. Решите неравенство

(х+11)(х+3)(х-8)0.

Ответы:

1. Иванов Сергей, Карпов Тимофей, Марков Андрей, Петров Алексей.

2. 8 семилитровых бидона и 10 пятилитровых, или 3 семилитровых и 17 пятилитровых.

3. за 2 минуты.

4. 7243•29=65187+144860=270047

5. Из бочки наполнить ведро, затем черпаком из ведра отобрать 4 л и вылить в бочку. В результате в ведре останется 3 л. Из этого ведра вылить в черпак 3 л, а из бочки наполнить ведро. Из этого ведра дополнить черпак, т.е. отлить 1 л. В результате в ведре останется 6 л. Повторив такую же процедуру, наливают 6 л бензина во второе ведро.

6. х=70

7. а+3в

8. 3 и 5.

9. (х-2)(х-13); (9х-8)²

11. (-∞; -11)Ụ(-3; 8).

Результаты:

1. Задача на логику (4 балла)

2. Задача, решаемая методом подбора (3 балла)

3. Задача на скорость (3 балла)

4. Восстановите запись (4 балла)

5. Задача на логику (4 балла)

6. Найти х. (4 балла)

7. Сократите дробь (2 балла)

8. Решите систему уравнений (3 балла)

9. Разложите многочлен на множители (4 балла)

10. Постройте график функции (2 балла)

11. Решите неравенство (2 балла)

Максимально можно набрать 35 баллов.

Высокий уровень – 29-35 баллов.

Средний уровень – 18-28 баллов.

Низкий уровень – менее 18 баллов.

Приложение № 9

Рубежный диагностический материал

3 года обучения

1. Запиши число 260 тремя цифрами «4», используя знаки действий.

2. При каком значении с прямая х+у+с=0 касается окружности х²+у²=1?

3. Приведи к рациональному виду знаменатель дроби:

а-в ; 1 ; 2 ;

√а²-в² 3-2√2 √2х-1

4. Шахтёры спорят по поводу своих участков. Каждый участок имеет форму прямоугольного треугольника. Размеры этих треугольников не совпадают, но площади у них у всех одинаковы и составляют точно 3360 м². Катеты одного треугольника равны 140 и 48, а его гипотенуза – 148 м. У второго треугольника катеты равны 80 и 84, а гипотенуза – 116 м. Укажи длины сторон третьего треугольника при условии, что они выражаются целыми числами, а площадь этого треугольника равна площади первых двух треугольников?

5. Запишите уравнение сферы, проходящей через точки А(0;0;0), В(4;0;0), С(0;4;0), если её радиус равен 3.

6. Постройте развёртку фигуры, состоящей из комбинации тела вращения и многогранника. Изобразите саму фигуру.

Ответы:

1. 4^4+4=256

2. ±√2_ __ ____

3. √а-в ; 3+2√2 ; 2√2х-1

2х-1

1. катеты равны 30 и 224, а гипотенуза 226.

2. (х-2) ²+(у-2) ²+(z-1) ²=9 и (х-2) ²+(у-2) ²+(z+1) ²=9.

Результаты:

1. Запиши число (3 балла)

2. Найди значение с. (3 балла)

3. Приведи к рациональному виду знаменатель дроби (6 балла)

4. Задача, решаемая методом подбора (5 баллов)

5. Задача на составление и решение системы уравнений (6 балла)

6. Творческое задание. (7 баллов)

Максимально можно набрать 30 баллов.

Высокий уровень – 25-30 баллов.

Средний уровень – 15-24 баллов.

Низкий уровень – менее 15 баллов.

Приложение № 10

Итоговый диагностический материал

3 года обучения

1. Преобразовать в произведение sin x+ cos2x- sin3x.

2. В одном центральном учреждении имеется три свободных должности: директора департамента, начальника отдела и старшего инспектора. На эти три должности выдвинуты 4 кандидатуры. Сколько троек, отличающихся друг от друга, по крайней мере одним кандидатом, можно создать из четырёх кандидатов?

3. Чулки изготавливаются на двух фабриках. Первая фабрика изготавливает 80% всех пар чулок, а вторая оставшиеся. На 100 пар чулок первой фабрики в среднем 83 пары первого сорта, а на 100 пар чулок второго завода – только 63 пары первого сорта. Сколько пар чулок первого сорта находится в каждой сотне, поступающей в торговую сеть? Какова вероятность приобретения пары первого сорта, если в магазин поступает продукция только первой фабрики, только второй фабрики, и первой и второй фабрики?

4. Чайнворд «Геометрия»

▒	▒		6
▒	▒		▒	▒	▒	▒	▒	▒	▒
1	▒		▒			10			▒
	▒		▒		▒	▒	▒		▒	5
	▒	7	▒		▒	▒	▒		▒
	▒		▒		▒	▒	▒		▒
	▒		▒		▒	▒	▒		▒
2	▒		▒	▒	▒	▒	▒		▒	4
	▒		8			9			▒
	▒	▒	▒	▒	▒	▒	▒	▒	▒
			3

1.Единица измерения плоских углов и дуг. 2. Часть, отсекаемая от круга секущей. 3. Геометрическая фигура, ограниченная тремя взаимно пересе-кающимися прямыми. 4. Сторона прямоугольного треугольника. 5. Прибор для измерения и построения углов. 6. Расстояния от центра до любой точки окружности. 7. Часть круга, заключённая между двумя радиусами. 8. Парал-лелограмм, все стороны которого равны. 9. Прямая, делящая угол на две равные части. 10. Предложение, принимаемое без доказательства.

5. Разность между вторым и первым членами геометрической прогрессии равна 18, а разность между четвёртым и третьим – 162. Составить прогрессию.

Ответы:

1. 4cos2x sin(π/12-x/2) cos(π/12+x/2)

2. 4

тройки	I	II	III	IV
директор	1	1	1	2
начальник	2	2	3	3
инспектор	3	4	4	4

3. 83/100; 63/100; 0,83·80+0,63·20=0,79

4. 1.градус 2. сегмент. 3. треугольник. 4. катет 5. транспортир 6. радиус 7.

сектор 8. ромб 9. биссектриса 10. аксиома.

5. в1 =9, q=3. (в2 -в1 =18, в 4 - в 3 = 162; в 1(q-1)=18, в 1 q²(q-1)=162)

Результаты:

1. Преобразование тригонометрического выражения (5 баллов)

2. Задача из комбинаторики (5 баллов)

3. Задача по теории вероятности (5 баллов)

4. Чайнворд «Геометрия» (10 баллов)

5. Прогрессия (5 баллов)

Максимально можно набрать 30 баллов.

Высокий уровень – 25-30 баллов.

Средний уровень – 15-24 баллов.

Низкий уровень – менее 15 баллов

Приложение № 11

А-1 Анкета

по изучению мотивации обучающихся.

для 1 года обучения

Любишь ли ты математику ? Нет.

1. На уроках математики скучно, неинтересно.

2. Не люблю сам предмет, так как увлекаюсь другим предметом.

3. Не люблю решать задачи.

4. Не умею самостоятельно решать задачи.

5. Не понимаю материал учебника; не могу в нём самостоятельно разобраться.

6. Имею серьёзные пробелы в знаниях по предмету за предыдущие годы, что мешает усвоить новый материал.

7. Надо много запоминать механически, а у меня плохая память.

8. Предмет очень трудный.

9. На уроках математики очень строго спрашивают.

10. На уроках математики не очень строго спрашивают.

11. Не объективно оценивают знания.

12. Я не вижу смысла в её изучении, мне кажется, что учить математику не нужно.

13. Я не люблю выполнять домашнее задание.

14. Мало времени даётся на изучение материала.

15. Родители не могут помочь при подготовке домашнего задания.

16. Какая другая причина?

Да

1. Мне легко даётся математика.

2. Математика нужна при решении практических задач.

3. Математика – интересный , увлекательный предмет.

4. При изучении математики повышается точность рассуждений, представляется возможность научиться строго доказывать.

5. Учитель математики хорошо объясняет материал, помогает его понять

6. Мне нравится решать трудные задачи, это как игра.

7. Материал учебника изложен доступно, есть возможность самому в нём разобраться.

Приложение № 12

А-2 Анкета

для определения потребностей учащихся.

в начале каждого учебного года

Индивидуальная образовательная программа по математике

на новый учебный год.

План:

1) Зачем мне нужно заниматься математикой?

2) Чему я хочу научиться?

3) Какие темы я хочу изучать?

4) Какие задания, практические работы я предлагаю выполнить?

5) Мои самые интересные вопросы и проблемы?

6) Что я буду делать, как заниматься?

7) Что мне необходимо для занятий?

8) В чём будут состоять результаты занятий?

9) Как я предлагаю контролировать свои результаты?

Приложение № 13

Т-1 Тест – таблица

исследования логического математического аспекта мышления

Методика «Числовой ряд»

Ключ

№1	3	4	5	6	7	8				9	10
№2	5	10	15	20	25	30				35	40
№3	8	7	6	5	4	3				2	1
№4	9	9	7	7	5	5				3	3
№5	3	6	9	12	15	18				21	24
№6	8	2	6	2	4	2				2	2
№7	8	9	12	13	16	17				20	21
№8	27	27	23	23	19	19				15	15
№9	8	9	12	13	16	17				20	21
№10	1	2	4	8	16	32				64	128
№11	22	19	17	14	12	9				7	4
№12	4	5	7	10	14	19				25	32
№13	12	14	13	15	14	16				15	17
№14	24	23	21	20	18	17				15	14
№15	16	8	4	2	1	1/2				1/4	1/8
№16	18	14	17	13	16	12				15	11
№17	12	13	11	14	10	15				9	16
№18	2	5	10	17	26	37				50	65
№19	21	18	16	15	12	10				9	6
№20	3	6	8	16	18	36				38	76

Приложение № 14

Т-2 Тест

диагностики интеллектуальных способностей.

Числовой субтест Айзенка.

1. Продолжите числовой ряд. 18 20 24 32 …

2. Вставьте недостающее число.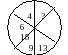

3. Продолжите числовой ряд. 212 179 146 113…

4. Вставьте недостающее число.

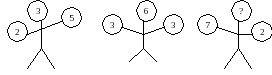
5. Продолжите числовой ряд. 6 8 10 11 14 14 …

6. Вставьте пропущенное число.

17 / 112 / 39

28 / / 49

7. Вставьте пропущенное число.

3 9 3

5 7 1

7 1 ?

8. Продолжите числовой ряд. 7 13 24 45 …

9. Вставьте пропущенное число.

234 / 333 / 567

345 / / 678

10. Продолжите числовой ряд. 4 5 7 19 …

11. Вставьте недостающее число.

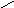
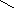
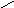
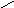
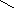
12. Продолжите числовой ряд. 6 7 9 13 21 …

13. Вставьте пропущенное число.

4 8 6

6 2 4

8 6 ?

14. Продолжите числовой ряд. 68 48 40 36 34 …

15. Вставьте пропущенное число.

			2	6
			54	18
?	9
81	27

16. Вставьте пропущенное число.

718 / 26 / 552

474 / / 226

17. Продолжите числовой ряд. 15 13 12 11 9 9 …

18. Вставьте пропущенное число.

9 4 1

6 6 2

1 9 ?

19. Вставьте пропущенное число. 11 12 14 ? 26 42

20. Вставьте пропущенное число.

8 5 2

4 2 0

9 6 ?

21. Вставьте пропущенное число.

341 / 250 / 466

282 / / 398

22. Вставьте пропущенное число.

23. Вставьте недостающее число.

24. Вставьте пропущенное число.

12 / 336 / 14

15 / / 16

25. Вставьте пропущенное число.

4 7 6

8 4 8

6 5 ?

26. Продолжите числовой ряд.

7 14 10 12 14 9 …

27. Вставьте недостающее число.

4 ?

4 ?

8 5 2 1 11 6 3 5

28. Вставьте пропущенное число. 17 / 102 / 12

14 / / 11

29. Продолжите числовой ряд. 172 84 40 18…

30. Продолжите числовой ряд. 1 5 13 29 …

Ответы:

1.	48	11.	5	21.	232
2.	24	12.	37	22.	18
3.	80	13.	7	23.	21
4.	5	14.	33	24.	480
5.	18	15.	3	25.	2
6.	154	16.	14	26.	19
7.	3	17.	6	27.	3
8.	86	18.	4	28.	77
9.	333	19.	18	29.	7
10.	35	20.	3	30.	61

Приложение № 15

Т-3 Тест

определения способности к абстрагированию

(умение выделять существенные признаки)

математических понятий.

Инструкция: обучающимся предлагается ряд математических терминов. Необходимо из пяти предложенных терминов выбрать два, которые точно определяют математическое понятие.

1. Геометрия (фигура, точка, свойства, уравнение, теорема)

2. Уравнение (корень, равенство, сумма, неизвестная, произведение)

3. Планиметрия (плоскость, квадрат, прямоугольник, фигура, прямая)

4. Треугольник (вершина, катет, сторона, центр, перпендикуляр)

5. Сумма (слагаемое, равенство, плюс, делитель, множитель)

6. Периметр (разность, сторона, сумма, фигура, прямоугольник)

7. Куб (угол, равенство, плоскость, сторона, вектор)

8. Дробь (делимое, делитель, частное, знаменатель, произведение)

9. Степень (корень, показатель, решение, основание, переменная)

10. Координата (плоскость, абсцисса, ось, ордината, прямая)

Ответы:

1. Геометрия (фигура, свойства)

2. Уравнение (равенство, неизвестная)

3. Планиметрия (плоскость, фигура)

4. Треугольник (вершина, сторона)

5. Сумма (слагаемое, плюс)

6. Периметр (сторона, сумма)

7. Куб (равенство, сторона)

8. Дробь (частное, знаменатель)

9. Степень (показатель, основание)

10. Координата (абсцисса, ордината)

Приложение № 16

Т-4 Тест

диагностики способности к обобщению

Методика исключения лишнего

							ответы
№1	8	-4	5	18	20		-4
№2	5	10	15	21	25		10
№3	8,7	-3	6	5,1	4		-3
№4	делимое	частное	плюс	деление	делитель		плюс
№5	3	6	9	22	15		22
№6	8	2	6	3	4		3
№7	основание	показатель	степень	произведение	разность		разность
№8	11	27	23	17	19		27
№9	прямо-угольник	тре-угольник	ромб	квадрат	паралле-лограмм		треу-гольник
№10	точка	отрезок	прямая	уравнение	плоскость		урав-нение
№11	десять	число	дробь	буква	пятнадцать		буква
№12	коорди-ната	ось	абс-циссса	фигура	ордината		фигура
№13	12	14	13	15	145		145
№14	24	23	21	20	18		23
№15	3х²	-4х	3х+8у	4у	18х²		3х+8у

Приложение № 17.

Правила математических игр.

Игра «Быки и коровы» или «Мастермайнд» (тестовая игра)

Играют двое. Каждый задумывает четырёхзначное число с разными цифрами, которое должен отгадать партнёр. Ход заключается в том, что отгадывающий называет определённое число, также четырёхзначное с разными цифрами. Если задуманное и названное числа имеют общие цифры, стоящие на одних и тех же местах, то такую ситуацию называют «быком» ( «б»). Если общие цифры есть, но стоят они на разных местах, то это «корова» ( «к»).В ответ на ход партнёра загадчик сравнивает своё число с названным и сообщает общее число «быков» и «коров». Выиграет тот, кто быстрее отгадает число противника. Ходы и ответы можно заносить в таблицу.

Н-р:

1 2 3 4 5 6

1568 1586 1658 2576 4539 3594

1б 1б 1к 1б 1б 4к

3к

Игра «Отгадай слово» (тестовая игра)

Играют двое. Один игрок задумывает слово из пяти букв, а другой должен его отгадать. С этой целью он называет одно за другим слова, состоящие из произвольного числа букв, на каждое из которых партнёр в ответ сообщает число, означающее, сколько раз буквы задуманного слова входят в названное; при этом каждая буква задуманного слова учитывается в ответе столько раз, сколько она содержится в названном. Например, задумано слово колба, противник назвал слово «оборона», тогда загадывающий называет число 5.

Игра «Морской бой» (тестовая игра)

Каждый из двух игроков рисует на клетчатой бумаге две доски размером 10Х10. На первой из них он расставляет свои карабли, а на второй разгадывает расположение кораблей противника.В состав флотилии входят 10 кораблей: один линкор (4х1, тетрамино), два крейсера (3х1, тримино), три эсминца (2х1, домино) и четыре катера (1х1, мономино). Корабли могут занимать любые поля доски, но не должны касаться друг друга ни сторонами, ни углами. Горизонтали доски обозначают числами от 1 до 10 (снизу вверх по левому краю), а вертикали - русскими буквами от а до к (слева направо по нижнему краю). После каждого выстрела (называют сначала букву, затем число) игрок получает от партнёра следующую информацию: «попал», «убил», «мимо».Игрок производит выстрелы до первого промаха. Корабль может быть не прямым, но должны палубы соприкасаться между собой одной стороной.

Игра «Знакомство»

Выбирается за основу какая-либо категория чисел. Например, числа, делящиеся на 3 и в записи которых есть цифра 3. Учащимися ведётся порядковый счёт. Вместо числа, попадающего под категорию, называется своё имя.

Игра «Наборщик» (игры со словами)

Берётся любое слово, и из его букв составляются другие слова. Используются имена существительные, нарицательные в исходной форме, в единственном числе, в именительном падеже и никаких ласкательно – уменьшительных. Выигрывает тот у кого окажется больше слов. Учитывается оригинальность слов и количество букв в них. Например, если играют 4 человека, то слово, найденное одним участником, оценивается в 3 очка, двумя – 2 очка, тремя – 1 очко, а если оно записано всеми, то просто вычеркивается (0 очков). (из слова «лекарство» придумано 180 слов.))

Игра «Анаграммы» (игры со словами)

Анаграмма – слово, составленное из всех букв данного слова. Например: колба – бокал, приказ –каприз, карта – карат – катар, клоун – колун – уклон – кулон, коршун – шнурок, материк – метрика, мошкара – ромашка, ротонда – торнадо, апельсин – спаниель, норматив – минотавр, хористка – акростих, вертикаль – кильватер, геометрия – геотермия, стационар – соратница, монограмма – номограмма, графология – голография, дозревание – раздвоение, ратификация – тарификация, старорежимность – нерасторжимость, выборочность – обрывочность, утонченность – уточненность, перемалывание - переламывание, автор – втора – рвота – тавро – товар, рост – сорт – торс - трос, вектор – корвет, корсет – сектор. Забавные анаграммы: схема смеха, фиалка калифа, ужимка мужика, реклама маклера, цитата Тацита, запонка напоказ, апостол полосат, волокита китолова. Вижу зверей – живу резвей, увидимся – удивимся, слепо топчут – после почтут.

ЭВМ и анаграммы. Чтобы найти анаграммы к словам, ЭВМ раполагает буквы, из которых состоит слово в алфавитном порядке, в словах, подходящих по количеству букв, проделывается та же операция. Затем сравнивается набор букв.

Игра «Палиндромы» (игры со словами)

Перевёртыши или полиндромы, - это слова, которые читаются одинаково слева направо и справо налево: поп, довод, доход, потоп, топот, наган, заказ, казак, шалаш, дом мод, «Аргентина манит негра», «И любит Сева вестибюли», «Лилипут сома на мосту пилил», «Удавы рвали лавры в аду», «Море могуче. В тон ему, шумен, отвечу Гомером: Море, веру буди – ярок, скор, я иду буревером…» (Д.Авалиани), «А роза упала на лапу Азора» (А.Фет), «Я иду с мечём, судия» (Г.Державин)

Игра «Каркас» (игры со словами)

Известна древняя головоломка, в которой надо найти набор слов, использующий все 33 буквы алфавита, причём по одному разу каждую. Например: бык, вяз, гной, дичь, плющ, съём, цех, шурф, этаж.

Игру «каркас» придумал А.Битман. Играющие фиксируют несколько согласных, а гласные (а также й, ъ ,ь) подбирают произвольно. Например буквы К, Н, Т. Тогда: канат, танк, кнут, ткань, тоника, нытик…

Игра «Метаграммы и цепочки слов» (игры со словами)

Метаграмма данного слова получается заменой одной из его букв на другую. Игра заключается в нахождении цепочки метаграмм, соединяющей два заданных слова. Например: коза- поза- полк- волк, или коза- лоза- луза- лупа- липа- лиса…

Можно соревноваться в количестве метаграмм для того или иного слова. Так, дом, ком, лом, сом, том, дым, дог, док, дол. Или кочка, дочка, мочка, качка, кичка, кучка, корка, кошка.

Игра «Ассоциации» (игры со словами)

Два слова или понятия будем считать ассоциативно связанными, если между ними есть что-то общее. Необходимо найти кратчайшую цепочку ассоциативных переходов между двумя данными словами. Например, небо и чай. Небо – земля - вода - питьё – чай.

Игра «Балда» (игры со словами)

Первый игрок называет произвольную букву, второй добавляет букву слева или справа, имея в виду некоторое слово. Следующий игрок также приписывает букву в любое место, имея в виду своё слово, и т. д. Тот, кто очередным ходом вынужден закончить слово, либо вообще не может приписать никакой буквы (потому, что не догадывается как продолжить слово), проигрывает кон и в наказание получает букву «б». При вторичном проигрыше «ба» и т. д. до слова «балда».

Шахматная игра «ход конём»

Требуется обойти конём все поля обычной шахматной доски так, чтобы ни одно из них не посетить дважды. Известно более 30 миллионов маршрутов.

Игры на необычных досках (шахматы)

• Доска 5х5 является минимальной, максимальная 12х12, есть прямоугольные доски 16х12.

• Шахматы на параллельных досках Игра ведётся одновременно на двух досках расположенных одна над другой. На каждой плоскости ходы обычные, фигуры могут перемещаться и в пространстве – с одной доски на другую. Ферзь в пространстве ходит как король, пешке разрешается менять плоскость только при взятии. Можно вторую плоскость образовать с помощью прозрачных стаканов.

• Гексагональные (шестигранные доски и поля) шахматы. Доска имеет форму шестигранника, по 6 полей на каждой стороне. Поля трёх цветов: белый, серый, чёрный. Полей 91.

Сказочные шахматы

• Шахматы с шахами и без шахов. Игра «до первого шаха». Выигрывает тот, кто первым объявляет шах. В игре «шахматы без шахов» объявлять простой шах запрещено. Первый же шах должен быть одновременно и матом.

• Поддавки. Основная задача игроков – избавиться от всех фигур. Мат отсутствует. Брать можно любую фигуру, включая короля.

Математические игры на шахматной доске

• Конь и верблюд. В углу доски n х n (n≥4) стоит конь, которым противники ходят по очереди. Первый игрок перемещает его как обычного коня, но с двойным ходом (2 хода подряд), а второй – как верблюда, то есть на три поля вдоль одной линии и на одно поле вдоль другой. «Белые» начинают и стремятся поставить фигуру в противоположный угол доски, а «чёрные стараются помешать им.

• Кошки – мышки. У первого игрока всего одна фигура – мышка, а у другого несколько фигур – кошек. Мышка и кошки ходят одинаково – на одно поле по вертикале или горизонтали. Если мышка оказалась на краю доски, то очередным ходом она спрыгивает с неё и убегает от кошек, если кошка и мышка попадают на одно поле, то кошка съедает мышку. Мышка стоит на середине поля, в первый ход она делает два шага. Кошек 2-3 стоят где угодно.