СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Axborotlarni raqamlar vositasida tasvirlash
Категория:
Информатика
03.04.2020 18:10












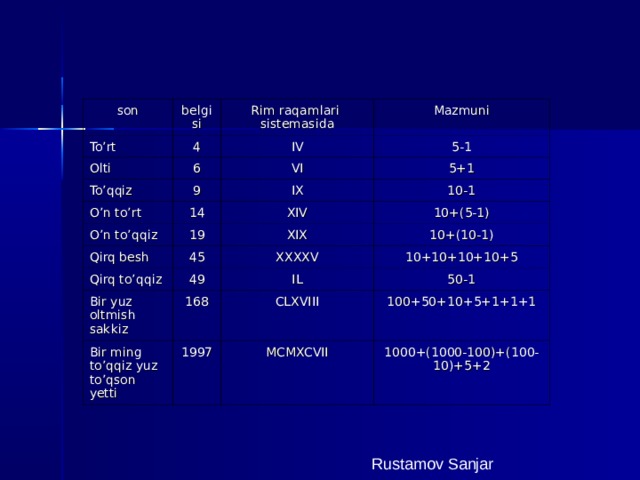
 belgi bilan 5 raqami V belgi bilan 10 soni X belgi bilan 50 soni L belgi bilan 100 soni C belgi bilan 500 soni D belgi bilan 1000 soni M belgi bilan Ular orasida boshqa sonlar miqdor jihatdan katta bo’lganidan ma’lum sonni ayirish yoki miqdor jihatdan kichik bo’lganiga biror sonni qo’shish ko’rinishida belgilanadi. Rustamov Sanjar " width="640"
belgi bilan 5 raqami V belgi bilan 10 soni X belgi bilan 50 soni L belgi bilan 100 soni C belgi bilan 500 soni D belgi bilan 1000 soni M belgi bilan Ular orasida boshqa sonlar miqdor jihatdan katta bo’lganidan ma’lum sonni ayirish yoki miqdor jihatdan kichik bo’lganiga biror sonni qo’shish ko’rinishida belgilanadi. Rustamov Sanjar " width="640"