Банк контрольных работ по геометрии 7 класс

Контрольная работа № 1

по теме «Начальные геометрические сведения»

1. Три точки В, С, и D лежат на одной прямой а. Известно, что ВD = 17 см, DC = 25 см. Какой может быть длина отрезка ВС?

2. Сумма вертикальных углов MOE и DOC, образованных при пересечении прямых МС и DЕ, равна 204°. Найдите угол МОD.

3. С помощью транспортира начертите угол, равный 78°, и проведите биссектрису смежного с ним угла. Укажите равные углы.

Контрольная работа № 1

по теме «Начальные геометрические сведения»

1. Три точки М, N, и K лежат на одной прямой а. Известно, что MN = 15 см, NK = 18 см. Каким может быть расстояние МK?

2. Сумма вертикальных углов АОВ и COD, образованных при пересечении прямых АD и ВС, равна 108°. Найдите угол ВОD.

3. С помощью транспортира начертите угол, равный 132°, и проведите биссектрису смежного с ним угла. Укажите равные углы.

Контрольная работа № 2

по теме «Треугольники. Признаки равенства треугольников»

1. Отрезки АВ и СD пересекаются в точке О, являющейся серединой каждого из них. Докажите, что: а) треугольники АОD и ВОС равны; б) 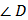_AО = _СВО.

2. Луч AD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что _ADB = _ADC. Докажите, что АВ = АС.

3. Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ₁ к боковой стороне АС.

Контрольная работа № 2

по теме «Треугольники. Признаки равенства треугольников»»

1. Отрезки МЕ и РК пересекаются в точке D, являющейся серединой каждого из них. Докажите, что: а) треугольники РDЕ и КDМ равны; б) _PED =_ KMD.

2. На сторонах угла D отмечены точки М и К так, что DM = DK. Точка Р лежит внутри угла D и РК = РМ. Докажите, что луч DР – биссектриса угла MDK.

3. Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту АН из вершины угла А.

Контрольная работа № 3

по теме «Параллельные прямые».

1. На рисунке прямые a и b параллельны, _1 = 55°. Найдите _2.

2. Отрезки АС и BD пересекаются в их общей середине точке О. Докажите, что прямые АВ и CD параллельны.

3. Отрезок DM – биссектриса треугольника CDE. Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N. Найдите углы треугольника DMN, если _СDЕ =68°.

Контрольная работа № 3

по теме «Параллельные прямые».

1. На рисунке прямые a и b параллельны, _1 = 115°. Найдите _2.

2. Отрезки АD и BC пересекаются в их общей середине точке М. Докажите, что прямые АС и ВD параллельны.

3. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне AB и пересекающая сторону AC в точке F. Найдите углы треугольника ADF, если _BAC =72°.

Контрольная работа № 4

по теме «Соотношения между сторонами и углами треугольника»

1. В треугольнике АВС АВ ВС АС. Найдите _ А, _ В, _ С, если известно, что один из углов треугольника равен 120°, а другой 40°.

2. В треугольнике CDE точка М лежит на стороне СЕ, причем _ CMD острый. Докажите, что DE DM.

3. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.

Контрольная работа № 4

по теме «Соотношения между сторонами и углами треугольника»

1. В треугольнике АВС АВ ВС АС. Найдите _ А, _ В, _ С, если известно, что один из углов треугольника прямой, а другой равен 30°.

2. В треугольнике MNP точка K лежит на стороне MN, причем _ NKP острый. Докажите, что KP MP.

3. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.

Контрольная работа № 5

по теме «Прямоугольный треугольник. Геометрические построения».

1. Дано: 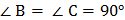_, AB = CD (Рис. 1).

Доказать: _.

1. В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NK в точке О, причем ОК = 9 см. Найдите расстояние ОН от точки О до прямой MN.

2. Постройте прямоугольный треугольник по гипотенузе и острому углу.

Контрольная работа № 5

по теме «Прямоугольный треугольник. Геометрические построения»

1. Дано: _, AD = BC (Рис. 2).

Доказать: AB = DC.

1. В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причем FC = 13 см. Найдите расстояние FH от точки F до прямой DE.

2. Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.

Итоговая контрольная работа по геометрии за 7 класс.

Вариант 1.

Часть I

1. Сумма углов равна 180, если они…

1) являются смежными; 2) являются вертикальными;

3) являются накрест лежащими; 4) являются развернутыми.

1. Две прямые, которые пересекаются под углом 90, являются…

1) смежными; 2) вертикальными;

3) параллельными; 4) перпендикулярными.

1. Треугольник называется равнобедренным, если у него…

1) все стороны равны; 2) две стороны равны;

3) все углы равны; 4) один угол равен 90⁰

1. Первый признак равенства треугольников называется…

1) по трём сторонам; 2) по стороне и прилежащим углам;

3) по трём углам; 4) по двум сторонам и углу между ними.

1. Прямые параллельны, если равны…

1) вертикальные углы; 2) смежные углы;

3) соответственные углы; 4) односторонние углы.

1. В треугольнике ABC A=C=50. Установите вид треугольника ABC.

1) равносторонний; 2) равнобедренный;

3) прямоугольный; 4) тупоугольный

1. Сторона прямоугольного треугольника, прилежащая к прямому углу называется…

1) боковой стороной; 2) гипотенузой;

3) основанием; 4) катетом.

1. Неравенствами треугольника ABC называются…

1) ABBC+AC; BCAB+AC; ACBC+AB.

2) AB

3) ABBC-AC; BCAB-AC; ACBC-AB.

4) AB

1. Биссектрисой угла называется луч, который исходит из вершины угла, …

1) и делит угол пополам;

2) и делит отрезок пополам;

3) и делит сторону пополам;

4) и перпендикулярно основанию.

Часть II

1. Найдите третий угол треугольника, если два его угла 36 и 57.

1) 36; 2) 57; 3) 93; 4) 87

1. Найдите углы при основании равнобедренного треугольника, если угол при вершине равен 82.

1) 82 и 164; 2) 49 и 49; 3) 82 и 36; 4) 98 и 98

1. В ABC проведена высота CD. Найдите углы DBC, если B=66.

1) 48, 66 и 66; 2) 24, 66 и 90;

3) 57, 57 и 66; 4) 24, 36 и 90

Часть III

1. Один из углов прямоугольного треугольника равен 60 ⁰, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу.

Итоговая контрольная работа по геометрии за 7 класс.

Вариант 2.

Часть I

1. Углы равны, если они…

1) являются смежными; 2) являются вертикальными;

3) являются параллельными; 4) являются односторонними.

1. Две прямые, которые не пересекаются, являются…

1) смежными; 2) вертикальными;

3) параллельными; 4) перпендикулярными.

1. Треугольник называется равносторонним, если у него…

1) все стороны равны; 2) две стороны равны;

3) все углы равны; 4) два угла равны.

1. Третий признак равенства треугольников называется…

1) по трём сторонам; 2) по стороне и прилежащим углам;

3) по трём углам; 4) по двум сторонам и углу между ними.

1. Прямые параллельны, если сумма…равна 180.

1) смежных углов; 2) накрест лежащих углов;

3) соответственных углов; 4) односторонних углов.

1. В треугольнике ABC A=C=60. Установите вид треугольника ABC.

1) равносторонний; 2) равнобедренный;

3) прямоугольный; 4) тупоугольный

1. Сторона прямоугольного треугольника, противолежащая прямому углу называется…

1) боковой стороной; 2) гипотенузой;

3) основанием; 4) катетом.

1. Неравенствами треугольника ABC называются…

1) ABBC+AC; BCAB+AC; ACBC+AB.

2) ABBC-AC; BCAB-AC; ACBC-AB.

3) AB

4) AB

1. Медианой треугольника называется отрезок, соединяющий …

1) середины сторон треугольника;

2) вершину треугольника и середину одной из сторон;

3) середины двух сторон треугольника;

4) вершину треугольника и середину противолежащей стороны.

Часть II

1. Найдите третий угол треугольника, если два его угла 65⁰ и 37⁰.

1) 37⁰; 2) 65⁰; 3) 78⁰; 4) 102⁰;

1. Найдите углы при основании равнобедренного треугольника, если угол при вершине равен 38.

1) 71 и 71; 2) 38 и 76; 3) 38 и 104; 4) 142 и 142

1. В ABC проведена высота BD. Найдите углы BDC, если C=54.

1) 54, 54 и 72; 2) 36, 54 и 90;

3) 36, 36 и 102; 4) 46, 54 и 90.

Часть III

1. Один из углов прямоугольного треугольника равен 60 ⁰, а меньший катет равен 28 см. Найдите гипотенузу.