ВСТУПИТЕЛЬНЫЕ ЭКЗАМЕНЫ В 10 КЛАСС
БИЛЕТЫ ПО МАТЕМАТИКЕ
Билет № 1
1.Система двух линейных уравнений с двумя переменными и ее решение.
2.Арифметическая прогрессия. Формулы n-го члена и суммы n первых членов арифметической прогрессии.
3. Теорема о вписанном угле в окружность.
4. Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма?
Билет № 2
1.Степень с натуральным показателем и ее свойства.
2. Линейное уравнение и его решение. Решение уравнений, сводящихся к линейным (на конкретных примерах).
3. Теорема о сумме углов треугольника.
4. Имеется два сплава. Первый сплав содержит 10% никеля, второй – 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Билет № 3
1. Степень с целым показателем и ее свойства.
2.Геометрическая прогрессия. Формулы n-го члена и суммы n первых членов геометрической прогрессии.
3. Свойства прямоугольника, ромба и квадрата.
4. Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Билет № 4
1. Признаки делимости на 2, 3, 5, 9, 10.
2. Функция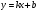 , ее свойства и график.
, ее свойства и график.
3. Признаки подобия треугольников.
4. Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 375 литров она заполняет на 10 минут быстрее, чем первая труба заполняет резервуар объемом 500 литров?
Билет № 5
1. Квадратное уравнение и его решение. Формулы корней квадратного уравнения.
2. Функция 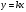 , ее свойства и график.
, ее свойства и график.
3. Признаки параллельности прямых.
4. Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из A вB. Найдите скорость велосипедиста на пути из A в B. Ответ дайте в км/ч.
Билет № 6
1. Линейные неравенства и их решение. Решение систем линейных неравенств (на конкретных примерах).
2. Функция 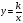 , ее свойства и график.
, ее свойства и график.
3. Свойства биссектрисы угла треугольника.
4. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Билет № 7
1. Формулы сокращенного умножения:
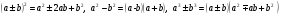
2. Функция 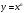 , ее свойства и график (n=2,3).
, ее свойства и график (n=2,3).
3. Свойства параллелограмма.
4. На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
Билет № 8
1. Квадратный трехчлен, разложение его на множители.
2. Геометрическая прогрессия. Формулы n-го члена и суммы n первых членов геометрической прогрессии.
3. Свойства равнобедренного треугольника.
4. Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь – за 18 часов. За сколько часов мальчики покрасят забор, работая втроем?
ОТВЕТЫ К ЗАДАЧАМ БИЛЕТОВ.
1. Ответ: 190.
2. Ответ: 100.
3. Ответ: 18.
4. Ответ: 25.
5. Ответ: 7.
6. Ответ: 59.
7. Ответ: 25.
8. Ответ: 8.
Билет № 1
1.Система двух линейных уравнений с двумя переменными и ее решение.
2. Теорема о вписанном угле в окружность.
3. Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма?
Билет № 2
1.Степень с натуральным показателем и ее свойства.
2. Теорема о сумме углов треугольника.
3. Имеется два сплава. Первый сплав содержит 10% никеля, второй – 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Билет № 3
1. Степень с целым показателем и ее свойства.
2. Свойства прямоугольника, ромба и квадрата.
3. Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Билет № 4
1. Признаки делимости на 2, 3, 5, 9, 10.
2. Признаки подобия треугольников.
3. Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 375 литров она заполняет на 10 минут быстрее, чем первая труба заполняет резервуар объемом 500 литров?
Билет № 5
1. Квадратное уравнение и его решение. Формулы корней квадратного уравнения.
2. Признаки параллельности прямых.
3. Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из A вB. Найдите скорость велосипедиста на пути из A в B. Ответ дайте в км/ч.
Билет № 6
1. Линейные неравенства и их решение. Решение систем линейных неравенств (на конкретных примерах).
2. Свойства биссектрисы угла треугольника.
3. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Билет № 7
1. Формулы сокращенного умножения:
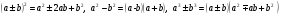
2. Свойства параллелограмма.
3. На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
Билет № 8
1. Квадратный трехчлен, разложение его на множители.
2. Свойства равнобедренного треугольника.
3. Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь – за 18 часов. За сколько часов мальчики покрасят забор, работая втроем?
Билет № 9
1. Корень п-ой степени его свойства.
2.Окружность, описанная около треугольника.
3. Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Билет № 10
1. Функция 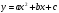 , её свойства и график.
, её свойства и график.
2. Окружность, вписанная в треугольник.
3. Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.
Билет № 11
1. Геометрическая прогрессия. Формулы n-го члена и суммы n первых членов геометрической прогрессии.
2. Свойства касательной к окружности.
3. При двух одновременно работающих принтерах расход бумаги составляет 1 пачку за 12 минут. Определите, за сколько минут израсходует пачку бумаги первый принтер, если известно, что он сделает это на 10 минут быстрее, чем второй.
Билет № 12
1. Функция 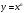 , ее свойства и график (n=2,3).
, ее свойства и график (n=2,3).
2. Теорема Пифагора.
3. Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
Билет № 13
1. Функция 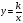 , ее свойства и график.
, ее свойства и график.
2. Значение синуса, косинуса и тангенса для углов 30º, 45º и 60º.
3. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на ![]() дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Билет № 14
1. Функция 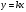 , ее свойства и график.
, ее свойства и график.
2. Формулы площади параллелограмма, треугольника и трапеции.
3. Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 14 килограммов изюма?
Билет № 15
1. Функция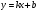 , ее свойства и график.
, ее свойства и график.
2. Сложение векторов и их свойства.
3. Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Билет № 16
1. Линейное уравнение и его решение. Решение уравнений, сводящихся к линейным (на конкретных примерах).
2. Скалярное произведение векторов и его свойства.
3. Четыре рубашки дешевле куртки на 8%. На сколько процентов пять рубашек дороже куртки?
Билет № 17
1. Арифметическая прогрессия. Формулы n-го члена и суммы n первых членов арифметической прогрессии.
2. Уравнение прямой и окружности.
3. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Билет № 18
1. Квадратное уравнение и его решение. Формулы корней квадратного уравнения.
2. Формула расстояния между двумя точками плоскости с заданными координатами.
3. Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 2 рабочих, а во второй — 12 рабочих. Через 3 дня после начала работы в первую бригаду перешли 8 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
Билет № 19
1. Функция 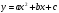 , её свойства и график.
, её свойства и график.
2. Свойство серединного перпендикуляра к отрезку.
3. Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша?
ОТВЕТЫ К ЗАДАЧАМ БИЛЕТОВ.
1. Ответ: 190.
2. Ответ: 100.
3. Ответ: 18.
4. Ответ: 25.
5. Ответ: 7.
6. Ответ: 59.
7. Ответ: 25.
8. Ответ: 8.
9. Ответ: 45.
10. Ответ: 10.
11. Ответ: 20.
12. Ответ: 16.
13. Ответ: 20.
14. Ответ: 133.
15. Ответ: 88.
16. Ответ: 15.
17. Ответ: 27.
18. Ответ: 8.
19. Ответ: 30







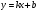 , ее свойства и график.
, ее свойства и график.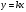 , ее свойства и график.
, ее свойства и график.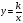 , ее свойства и график.
, ее свойства и график.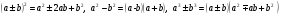
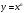 , ее свойства и график (n=2,3).
, ее свойства и график (n=2,3).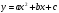 , её свойства и график.
, её свойства и график.









