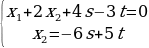СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Бир тектуу сызыктуу тендемелер системасы
Категория:
Алгебра
26.12.2024 19:05




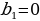
 болсо бир тектуу система дайыма биргелешкен болот, себеби
болсо бир тектуу система дайыма биргелешкен болот, себеби  =
= =
= нолдук (тривиалдык) чечими дайым жашайт.
нолдук (тривиалдык) чечими дайым жашайт.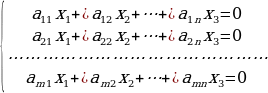
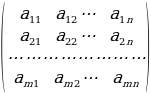 X=
X= 0=
0=
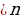

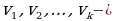 Фундаменталдык чечимдер системасынитузгон сызыктуу коз карандысыз векторлор;
Фундаменталдык чечимдер системасынитузгон сызыктуу коз карандысыз векторлор; 
 Каалаган эркин параметрлер
Каалаган эркин параметрлер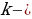 матрицанын рангы аркылуу аныкталаган чечимдердин эркиндигинин даражасы:
матрицанын рангы аркылуу аныкталаган чечимдердин эркиндигинин даражасы: 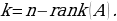
 анда системанын чечими жок б.а биргелешкен эмес.
анда системанын чечими жок б.а биргелешкен эмес. 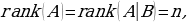 анда система жалгыз чечимге ээ.
анда система жалгыз чечимге ээ. анда система чексиз чечимге ээ болот. б.а
анда система чексиз чечимге ээ болот. б.а 

 A=
A=


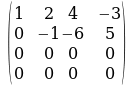

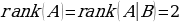

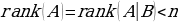 , анда бул бир тектуу система чексиз нолдук чыгарылыштарга ээ .
, анда бул бир тектуу система чексиз нолдук чыгарылыштарга ээ . негизги (базистик) озгормолор ;
негизги (базистик) озгормолор ; 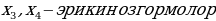 . Демек
. Демек  деп алсак болот.
деп алсак болот.