Четырёхугольники

Четырёхугольники

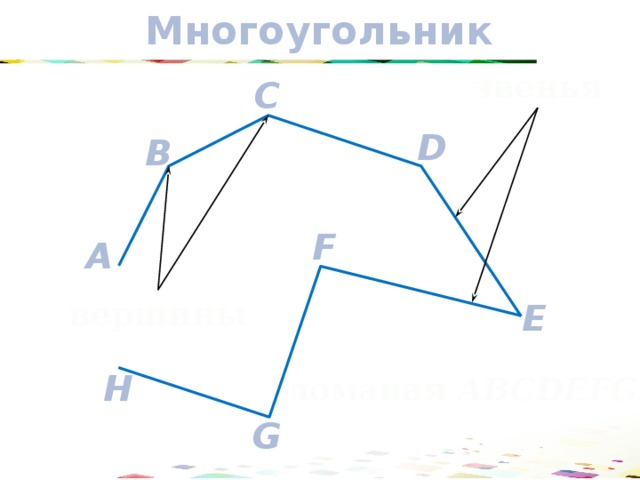
Многоугольник

звенья

C

D

B

F

A

вершины

E

H

ломаная ABCDEFGH

G

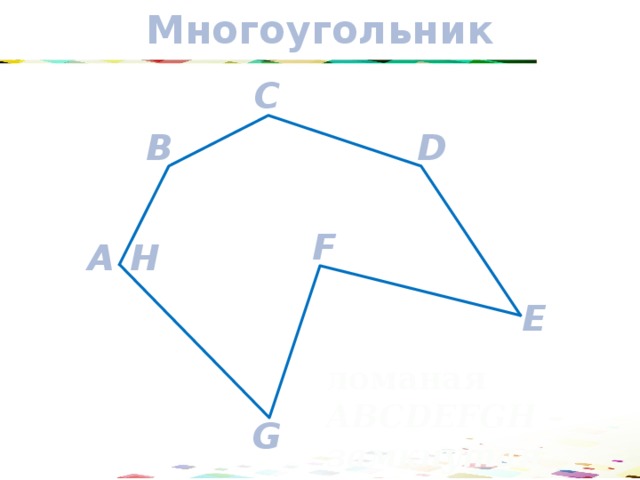
Многоугольник

C

D

B

F

A

H

E

ломаная ABCDEFGH – замкнутая

G

Многоугольник

Если несмежные звенья замкнутой ломаной не имеют общих точек, то эта ломаная называется многоугольником .

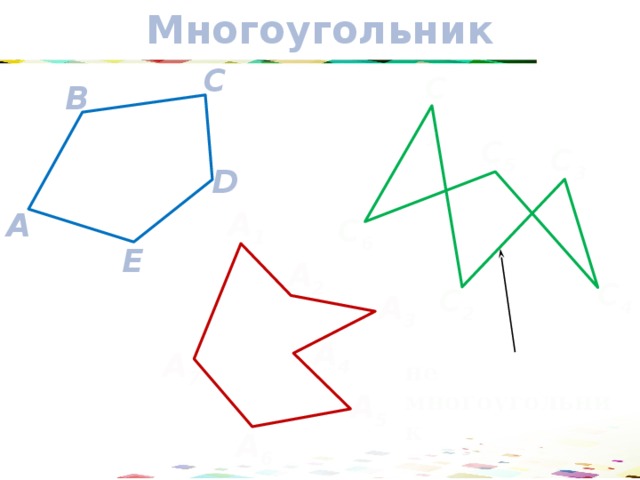
Многоугольник

C

С 1

B

С 5

С 3

D

А 1

A

С 6

E

А 2

С 4

С 2

А 3

А 4

А 7

не многоугольник

А 5

А 6

5

Многоугольник

Многоугольник разделяет плоскость на внутреннюю и внешнюю области.

внутренняя

внешняя

5

Многоугольник

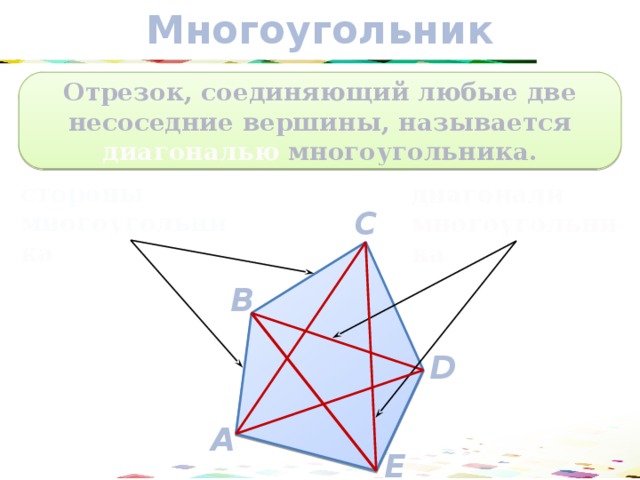
Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.

стороны многоугольника

диагонали

многоугольника

C

B

D

A

E

5

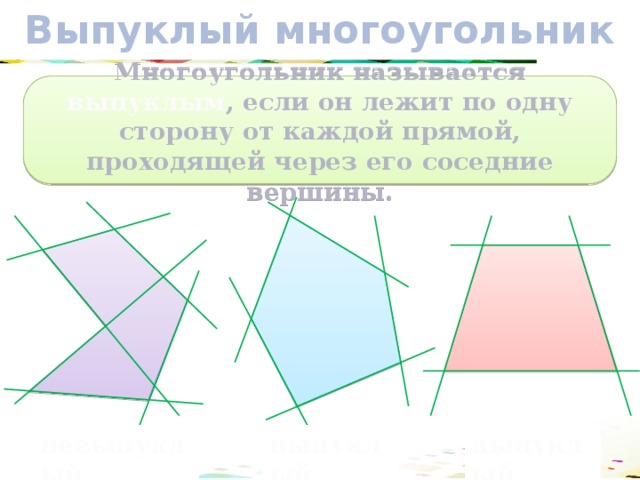
Выпуклый многоугольник

Многоугольник называется выпуклым , если он лежит по одну сторону от каждой прямой, проходящей через его соседние вершины.

выпуклый

выпуклый

невыпуклый

5

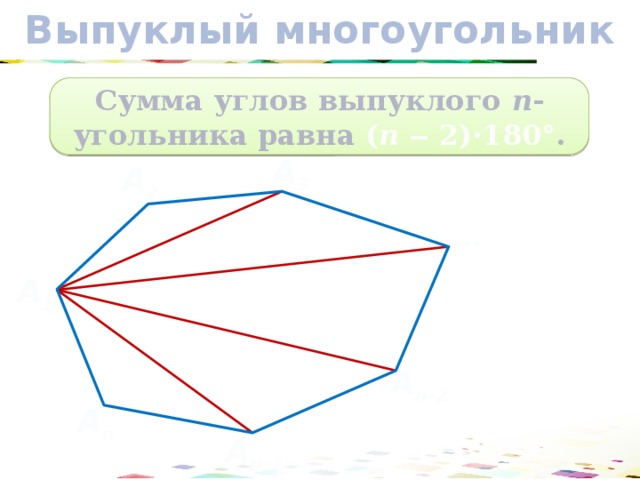
Выпуклый многоугольник

Сумма углов выпуклого n -угольника равна ( n ‒ 2)·180° .

А 3

А 2

…

А 1

А n-2

А n

А n-1

9

Выпуклый многоугольник

Внешним углом выпуклого многоугольника называется угол, смежный с углом многоугольника.

180°‒  1 + 180° ‒  2 + 180°‒  3 + … + 180°‒  n =

= n · 180° ‒ (  1 +  2 +  3 + … +  n ) =

= n · 180°‒ ( n ‒ 2) · 180°= 360°

3

Сумма внешних углов выпуклого многоугольника равна 360° .

2

…

1

n

9

Четырёхугольник

Две несмежные стороны четырёхугольника называются противоположными .

Четырёхугольники бывают выпуклые и невыпуклые

1

3

2

4

8

5

6

7

11

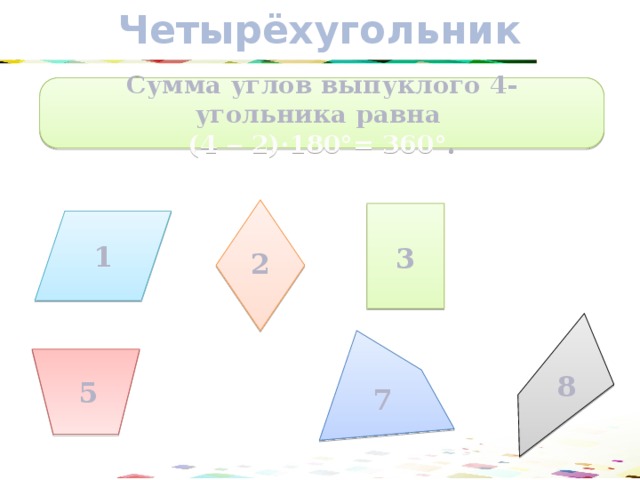
Четырёхугольник

Сумма углов выпуклого 4-угольника равна

(4 ‒ 2)·180°= 360° .

1

3

2

8

5

7

12

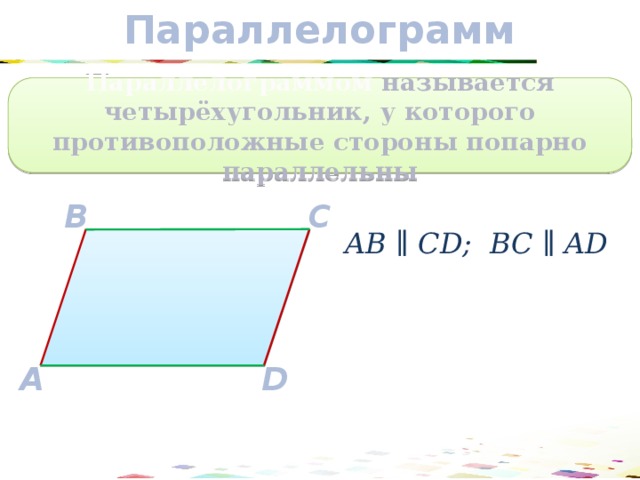
Параллелограмм

Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны

B

C

АВ ∥ CD; BC ∥ AD

A

D

12

Решите задачу

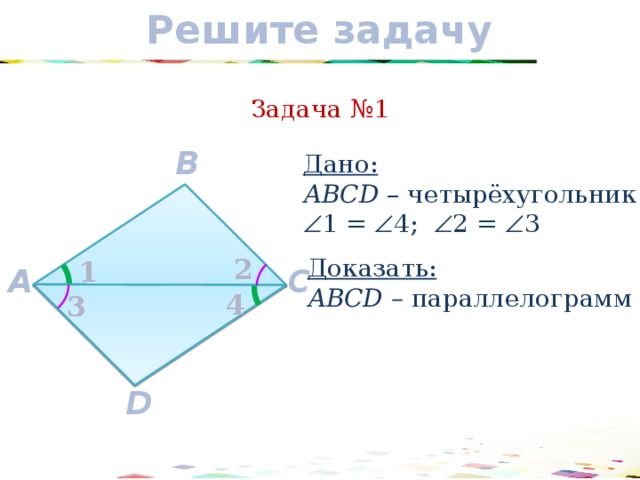
Задача №1

B

Дано:

АВCD – четырёхугольник

 1 =  4;  2 =  3

2

Доказать:

АВCD – параллелограмм

1

C

A

4

3

D

14

Решите задачу

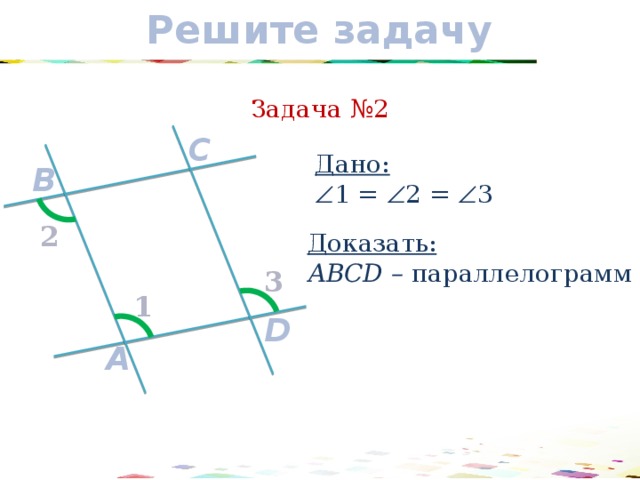
Задача №2

C

Дано:

 1 =  2 =  3

B

2

Доказать:

АВCD – параллелограмм

3

1

D

A

15

Решите задачу

Задача №3

Дано:

MNPQ – четырёхугольник

MN ∥ PQ;  M =  P

P

N

Доказать:

MNPQ – параллелограмм

Q

M

16

Решите задачу

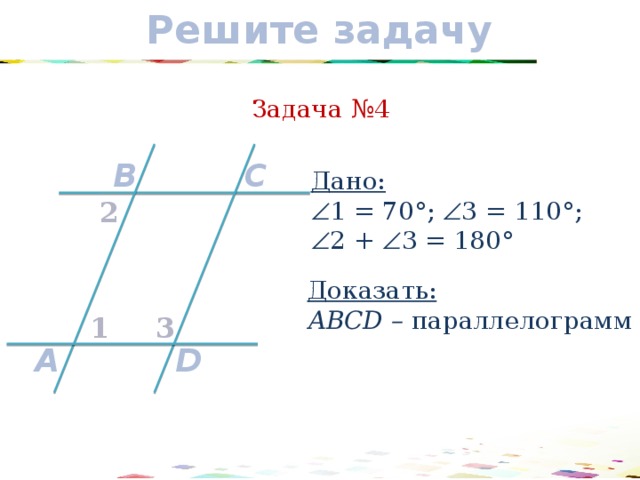
Задача №4

C

B

Дано:

 1 = 70°;  3 = 110°;

 2 +  3 = 180°

2

Доказать:

АВCD – параллелограмм

3

1

D

A

17

Свойства параллелограмма

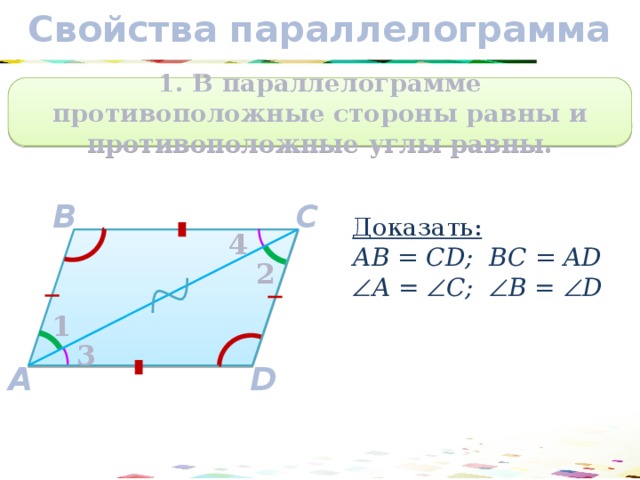
1. В параллелограмме противоположные стороны равны и противоположные углы равны.

B

C

Доказать:

АВ = CD; BC = AD

 А =  С;  В =  D

4

2

1

3

D

A

17

Свойства параллелограмма

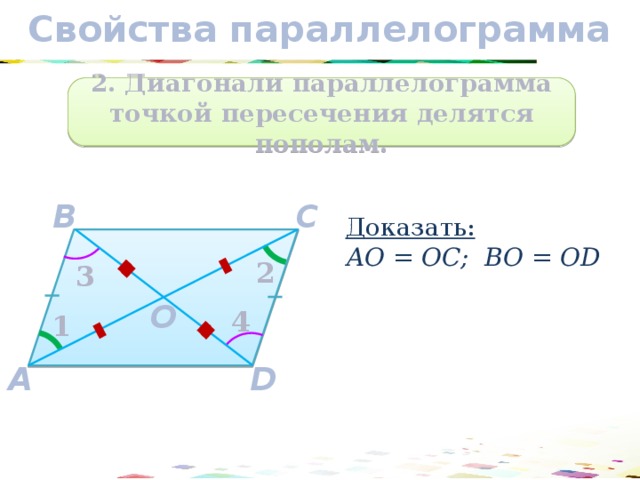
2. Диагонали параллелограмма точкой пересечения делятся пополам.

B

C

Доказать:

АО = ОC; BО = ОD

2

3

О

4

1

A

D

17

Признаки параллелограмма

1) Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник ‒ параллелограмм .

B

C

Дано:

АВ = CD; АВ ∥ СD

4

2

Доказать:

АВCD ‒ параллелограмм

1

3

D

A

17

Признаки параллелограмма

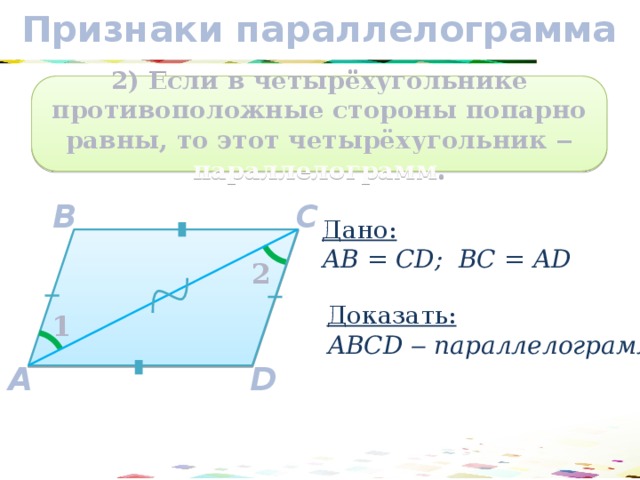
2) Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник ‒ параллелограмм .

B

C

Дано:

АВ = CD; ВС = АD

2

Доказать:

АВCD ‒ параллелограмм

1

D

A

17

Признаки параллелограмма

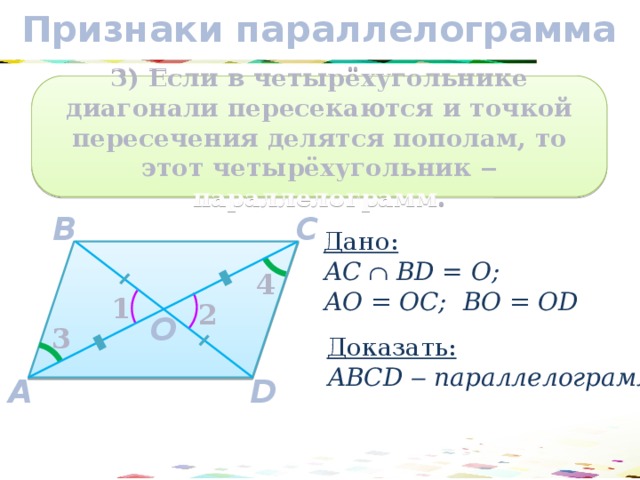
3) Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник ‒ параллелограмм .

B

C

Дано:

АС  ВD = О;

АО = ОC; BО = ОD

4

1

2

О

3

Доказать:

АВCD ‒ параллелограмм

D

A

17

Признаки параллелограмма

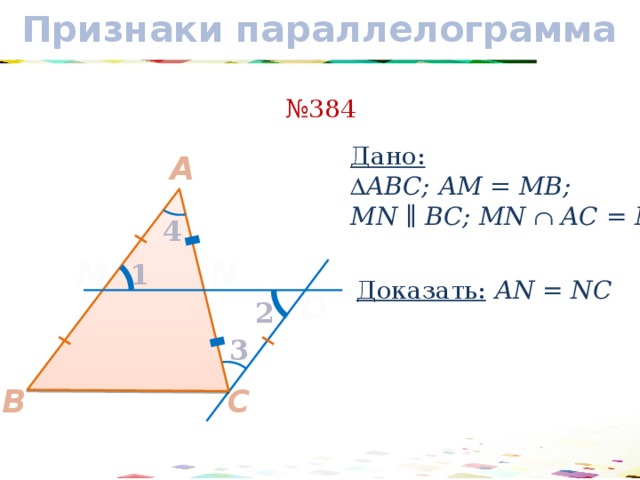
№ 384

Дано:

∆ АBС; АM = MB;

MN ∥ BC; MN  AC = N

A

4

N

M

1

Доказать: АN = NC

D

2

3

C

B

17

№ 385 Теорема Фалеса

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки

A 1

В 1

Дано: l 1 , l 2 ;

A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5 = …

A 1 B 1 ∥ A 2 B 2 ∥ A 3 B 3 ∥ A 4 B 4 …

Доказать:

B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B 5 = …

Доказательство:

1 случай, если l 1 ∥ l 2

A 2

В 2

A 3

В 3

A 4

В 4

l 1

l 2

17

№ 385 Теорема Фалеса

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки

A 1

В 1

Дано: l 1 , l 2 ;

A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5 = …

A 1 B 1 ∥ A 2 B 2 ∥ A 3 B 3 ∥ A 4 B 4 …

Доказать:

B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B 5 = …

Доказательство:

2 случай, если l 1 ∦ l 2

A 2

В 2

C

В 3

A 3

D

A 4

В 4

l 2

l 1

l

17

Фале́с Милетский

Фале́с  (др.-греч. Θαλῆς ὁ Μιλήσιος, 640/624  ‒ 548/545 до н.э.) ‒ древнегреческий философ и математик из Милета (Малая Азия).

Основатель милетской (ионийской) школы, с которой начинается история европейской науки. Традиционно считается основоположником греческой философии (и науки) ‒ он неизменно открывал список «семи мудрецов», заложивших основы греческой культуры и государственности.

17

Фале́с Милетский

Именем Фалеса названа геометрическая теорема о пропорциональных (равных) отрезках и параллельных прямых.

Считается, что Фалес первым сформулировал и доказал несколько геометрических теорем, а именно:

• вертикальные углы равны;
• равенство треугольников по одной стороне и двум прилегающим к ней углам;
• углы при основании равнобедренного треугольника равны;
• диаметр делит круг на две равные части;
• вписанный угол, опирающийся на диаметр, является прямым.

17

Фале́с Милетский

Фалес научился определять расстояние от берега до корабля, для чего использовал подобие треугольников. В основе этого способа лежит теорема, названная впоследствии теоремой Фалеса: если параллельные прямые, пересекающие стороны угла, отсекают равные отрезки на одной его стороне, то они отсекают равные отрезки и на другой его стороне.

Легенда рассказывает о том, что Фалес, будучи в Египте, поразил фараона Амасиса тем, что сумел точно установить высоту пирамиды, дождавшись момента, когда длина

тени палки становится равной её высоте, и тогда измерил длину тени пирамиды.

17

Решите задачу

Задача №5

Найти: х

120°

x

a

x+10°

60°

b

n

m

29

Решите задачу

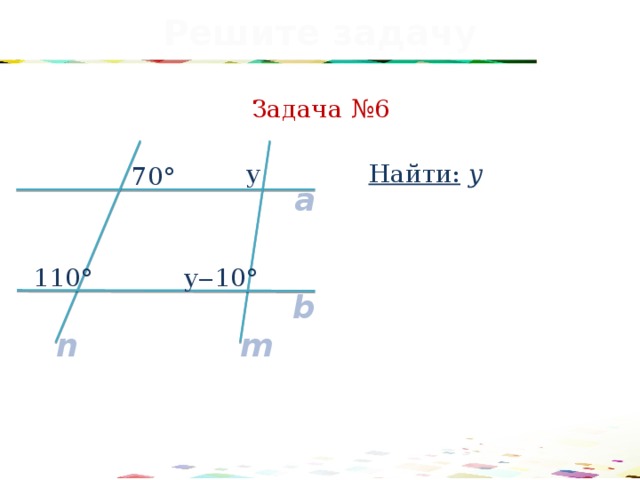
Задача №6

Найти: у

у

70°

a

110°

у‒10°

b

n

m

30

Решите задачу

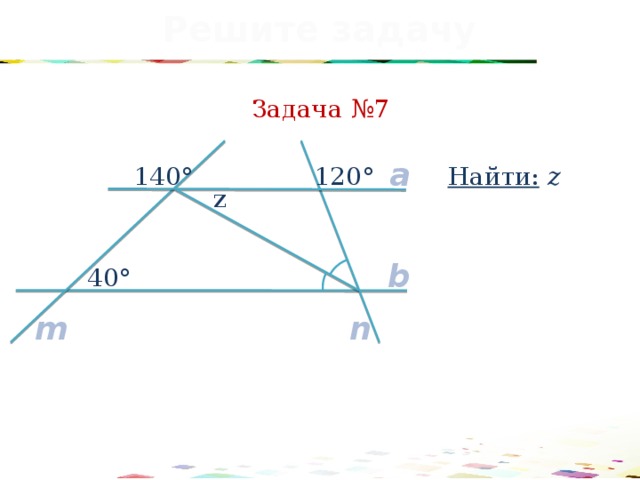
Задача №7

a

Найти: z

140°

120°

z

b

40°

m

n

31

Расшифруйте ребус

,

,

3

4

,

,

ия

,

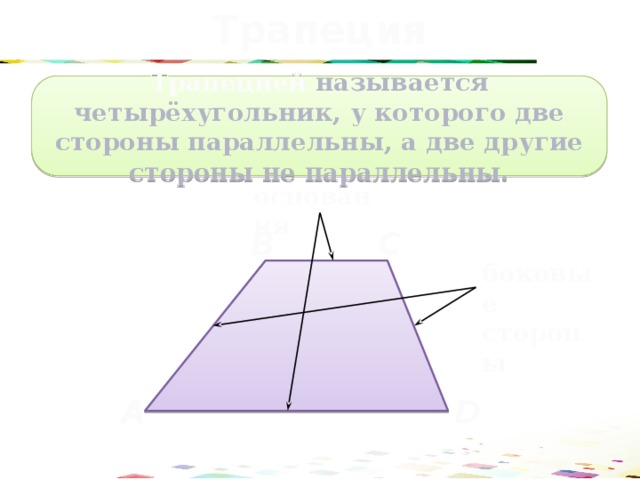
Трапеция

Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

основания

C

B

боковые стороны

A

D

33

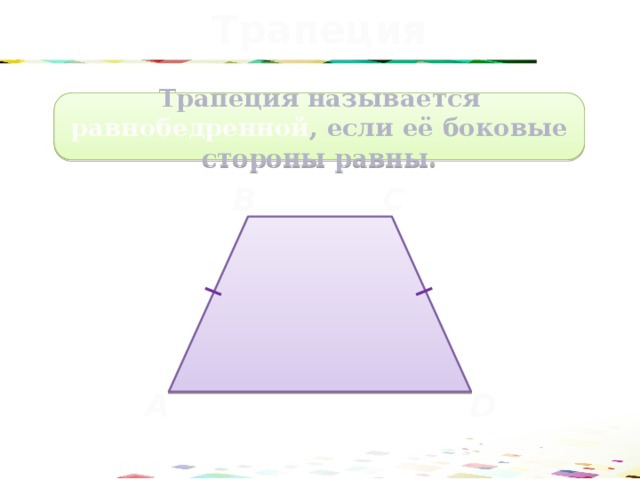
Трапеция

Трапеция называется равнобедренной , если её боковые стороны равны.

B

C

A

D

34

Трапеция

Трапеция, один из углов которой прямой, называется прямоугольной .

C

B

A

D

35

Трапеция

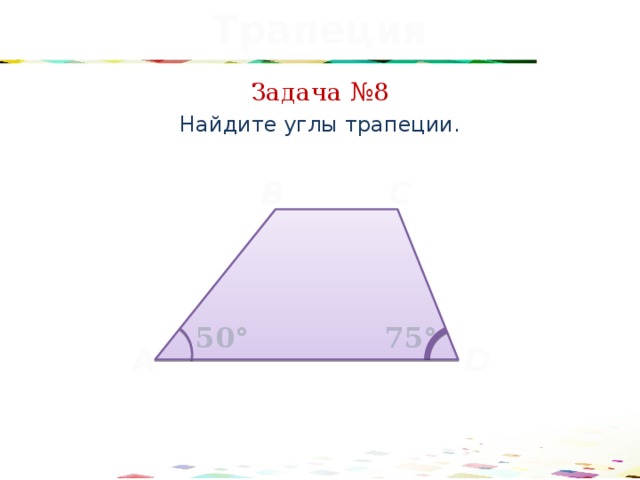
Задача №8

Найдите углы трапеции.

C

B

75°

50°

A

D

36

Трапеция

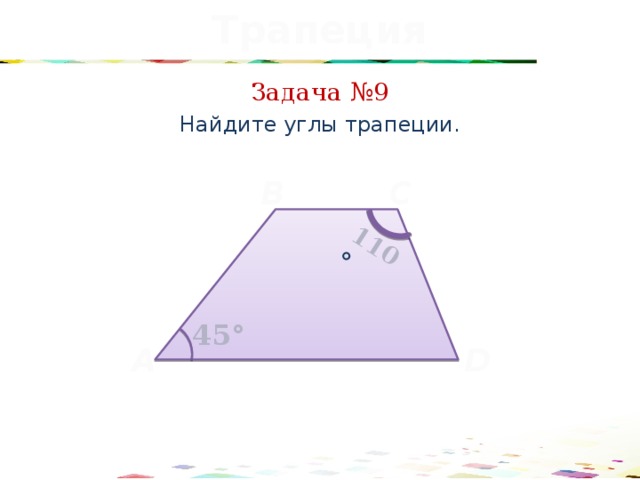
110 °

Задача №9

Найдите углы трапеции.

C

B

45°

A

D

37

Трапеция

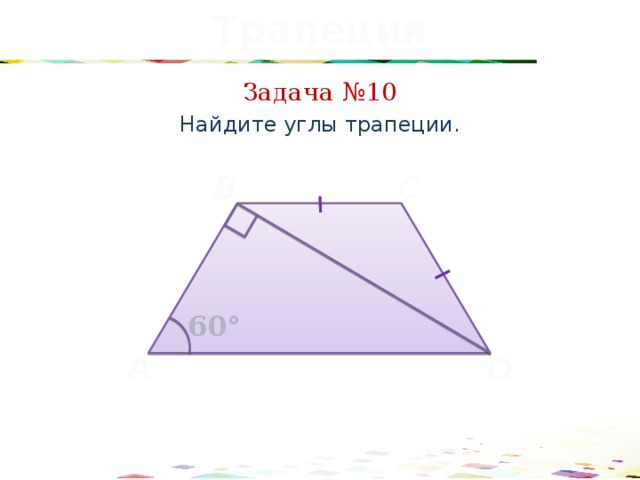
Задача №10

Найдите углы трапеции.

C

B

60°

A

D

38

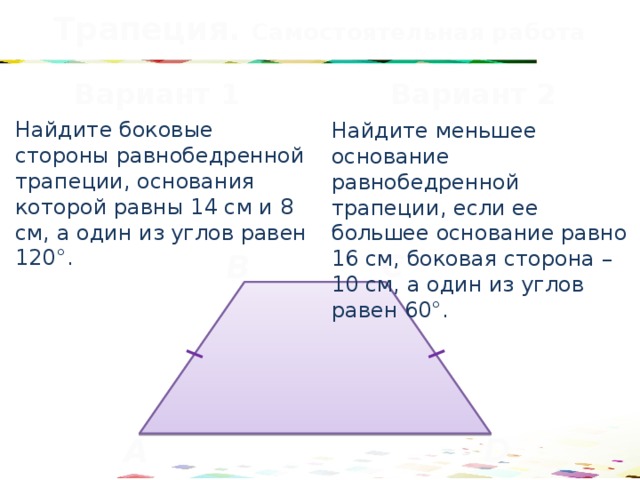
Трапеция. Самостоятельная работа

Вариант 1

Вариант 2

Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 120°.

Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая сторона – 10 см, а один из углов равен 60°.

C

B

D

A

39

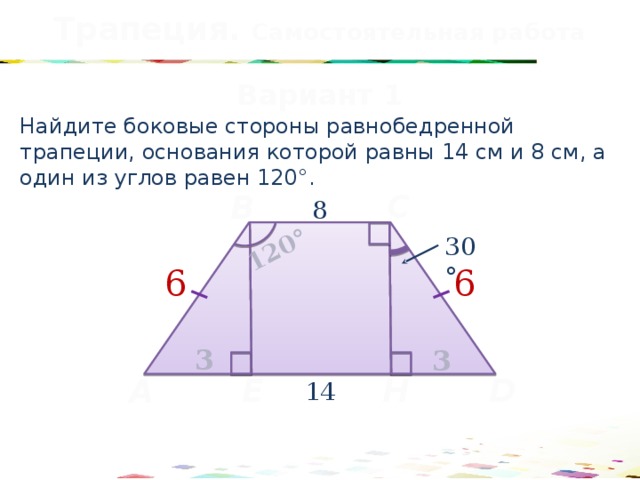
Трапеция. Самостоятельная работа

120°

Вариант 1

Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 120°.

C

B

8

30°

6

6

3

3

Н

Е

D

A

14

40

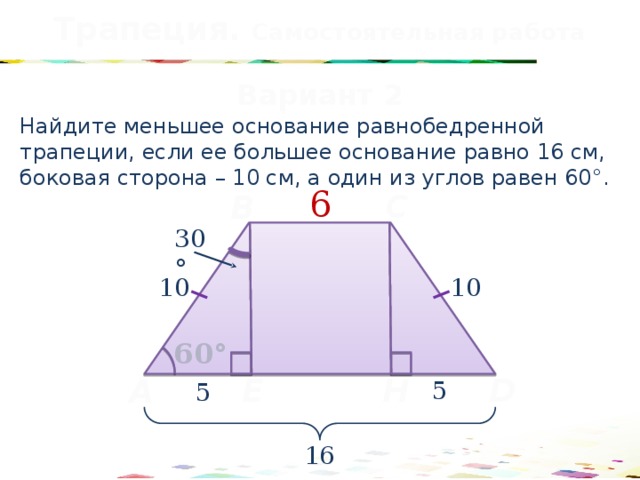
Трапеция. Самостоятельная работа

Вариант 2

Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая сторона – 10 см, а один из углов равен 60°.

6

C

B

30°

10

10

60°

Н

Е

D

A

5

5

16

41

Решите задачу

Задача №11

Найдите углы выпуклого четырёхугольника, если их градусные меры пропорциональны числам 1, 2, 3, 4.

х + 2х + 3х + 4х = 360°

10х = 360°

х = 36°

2х = 72°

3х = 108°

4х = 144°

3х

4х

х

2х

41

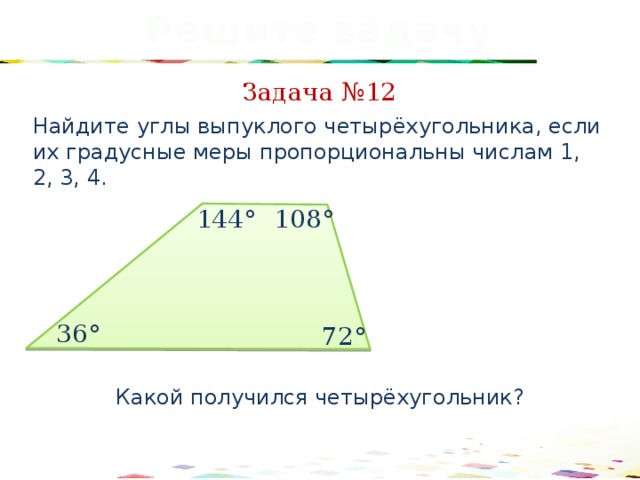
Решите задачу

Задача №12

Найдите углы выпуклого четырёхугольника, если их градусные меры пропорциональны числам 1, 2, 3, 4.

108°

144°

36°

72°

Какой получился четырёхугольник?

41

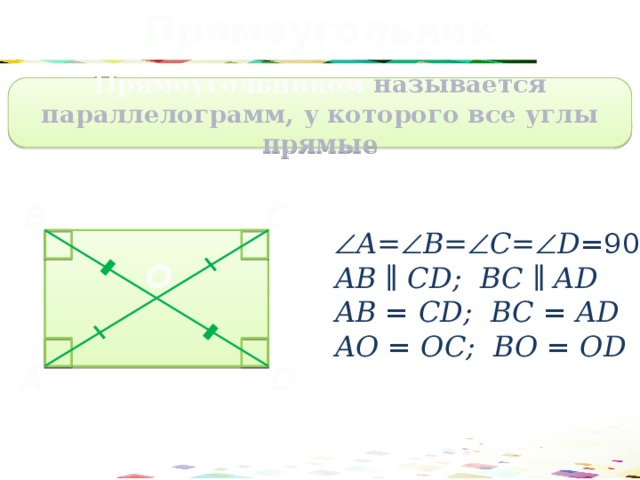
Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы прямые

B

C

 А=  В=  С=  D =90°

АВ ∥ CD; BC ∥ AD

АВ = CD; BC = AD

АО = ОC; BО = ОD

О

D

A

41

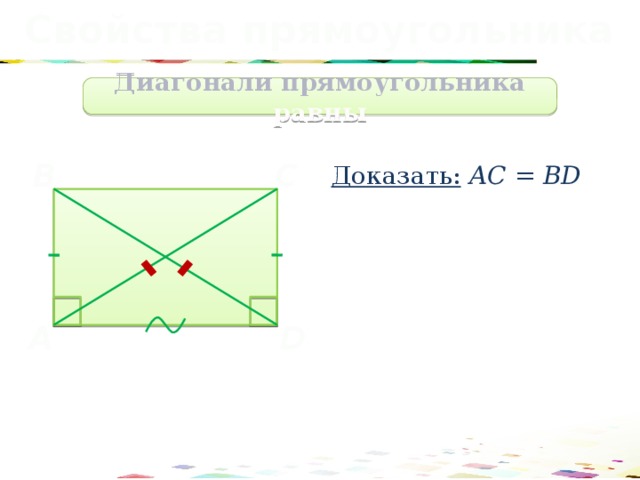
Свойства прямоугольника

Диагонали прямоугольника равны

B

C

Доказать: АС = BD

A

D

41

Признак прямоугольника

Если в параллелограмме диагонали равны, то этот параллелограмм - прямоугольник

B

C

Доказать: если в

параллелограмме ABCD

АС = BD , то ABCD - прямоугольник

D

A

41

Решите задачу

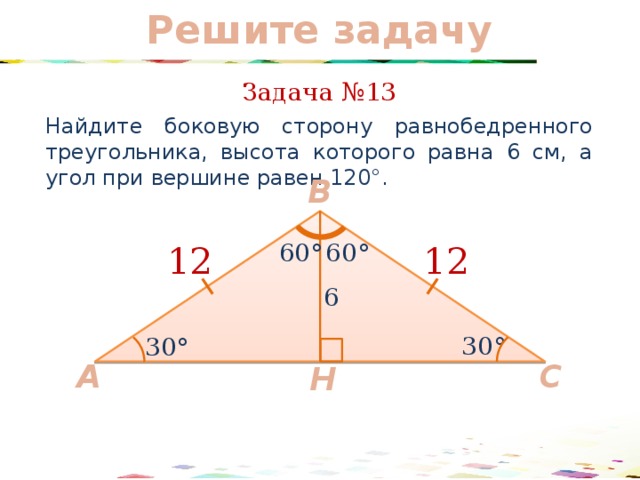
Задача №13

Найдите боковую сторону равнобедренного треугольника, высота которого равна 6 см, а угол при вершине равен 120°.

B

60°

60°

12

12

6

30°

30°

C

A

Н

41

Расшифруйте ребус

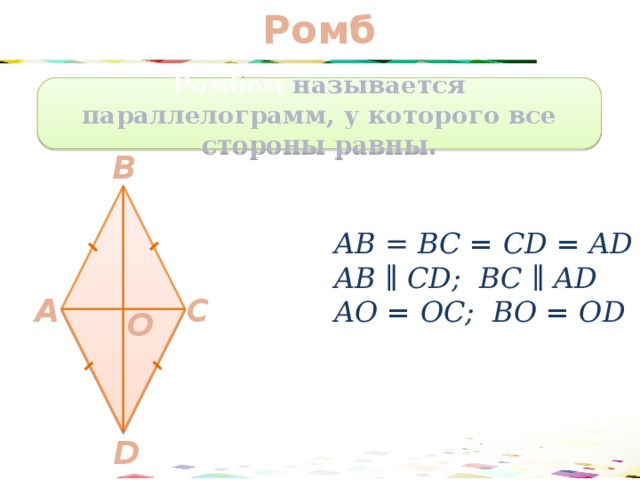
Ромб

Ромбом называется параллелограмм, у которого все стороны равны.

B

АВ = BC = CD = AD

АВ ∥ CD; BC ∥ AD

АО = ОC; BО = ОD

C

A

О

D

49

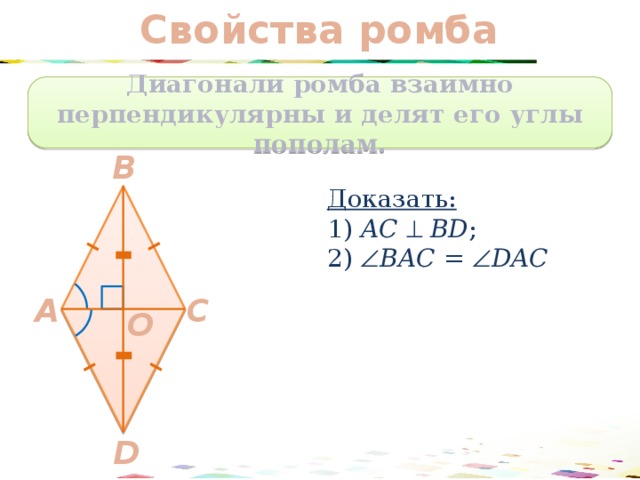
Свойства ромба

Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

B

Доказать:

1) АС  BD ;

2)  ВАС =  DAC

C

A

О

D

49

Расшифруйте ребус

К

2,3,1

2

о=а

51

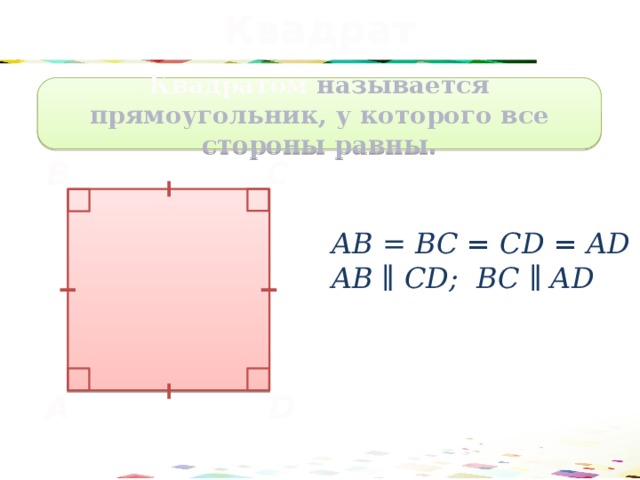
Квадрат

Квадратом называется прямоугольник, у которого все стороны равны.

C

B

АВ = BC = CD = AD

АВ ∥ CD; BC ∥ AD

D

A

51

Свойства квадрата

1) Все углы квадрата прямые.

2) Диагонали квадрата равны.

3) Диагонали взаимно перпендикулярны.

C

B

 А=  В=  С=  D =90°

АС = ВD; АС  ВD

О

D

A

51

Свойства квадрата

4) Диагонали точкой пересечения делятся пополам.

5) Диагонали делят углы квадрата пополам.

B

C

АО = ОC = BО = ОD

 1=  2=  3=  4=

=  5=  6=  7=  8=45°

5

4

3

6

О

1

7

2

8

D

A

51

Использованы ресурсы

• Геометрия. 7 – 9 классы: учеб. для общеобразоват. организаций / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – 6-е изд. – М.: Просвещение, 2016.
• Изучение геометрии в 7 – 9 классах: Пособие для учителей / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др. – 7-е изд. – М.: Просвещение, 2009.
• https:// ru.wikipedia.org/wiki/ ‒ Фалес Милетский
• http:// www.newworldencyclopedia.org/entry/File:Thales2.jpg ‒ Фалес Милетский
• https:// commons.wikimedia.org/wiki/File:Thales_theorem_6.png ‒ определение высоты пирамиды способом Фалеса