Числа и их Свойства. ЕГЭ Задания 19

Числа и их свойства

Базовый уровень

Задание №19

№ 1. Найдите наименьшее четырехзначное число, кратное 15, произведение цифр которого больше 40, но меньше 50

Пусть число имеет

вид abcd

40

Произведение цифр кратно 5, а значит равно 45

Так как число кратно 15,

значит кратно 3 и кратно 5

abc

Последняя цифра :

d= 0 или d= 5

abc =1

d= 0 не подходит, иначе произведение цифр =0

1

3

3

5

В 19

х

3

х

1

0

№ 2.Вычеркните в числе 123456 три цифры так, чтобы получившееся трехзначное число было кратно 35

Выполним подбор

35·3=105

35·5=175

35·7=245

Т.к. число кратно 35,

то кратно 5, оканчивается либо 0, либо 5

Вычеркиваем цифру 6, цифру 5 оставляем

Вычеркнем цифры 1 и 3

2

5

4

В 19

х

3

х

1

0

№ 3. Вычеркните в числе 123456 три цифры так, чтобы получившееся трехзначное число было кратно 27

Т.к. число кратно 27,

то кратно 9,

Проверим какое из чисел 126 и 135 кратно 27

Сумма цифр

кратна 9

1+2+6=9

1+3+5=9

• не кратно 27

135 кратно 27

1

3

5

В 11

х

3

х

1

0

№ 4. Найдите наименьшее трехзначное число. Которое при делении на 2 дает остаток 1, при делении на 3 дает остаток 2, а при делении на 5 дает остаток 4 и которое записано тремя различными нечетными цифрами

Числа, которые при делении на 5 дают в остатке 4, оканчиваются либо на 9, либо на 4, но 4 - четное

1, 3,5

1,3,7

Любое нечетное число при делении на 2 даст в остатке 1. Искомое число может состоять из:

1, 3,9

1,5,7

1, 5,9

1,9,7

3, 5,9

3,5,7

5,7,9

Рассмотрим числа

179, 359, 719, 539

Наименьшее: 179

Суммы цифр 1+5+9=15, 5+7+9=21 исключаем, как кратные 3

Группа цифр 1,3,9 также исключается

1+3+9 =13 13 – 2 =11

1+9+7 = 17 17-2=15

3+5+9=17 17-2=15

1

9

7

В 19

х

3

х

1

0

№ 5. Найдите наибольшее пятизначное число, которое записывается только цифрами 0, 5 и 7 и делится на 120

Искомое число оканчивается 0.

Т.к число делится на 4, то две последние цифры 0.

Т.к. число кратно 3, значит сумма цифр кратна 3 7+5+0+0+0 =12 кратно 3

7

5

0

0

0

В 11

х

3

х

1

0

№ 6. Найдите четырёхзначное число, кратное 4, сумма цифр которого равна их произведению

Среди цифр a, b, с и d

Не может быть трех единиц, 1+1+1+d=d –равенство невозможно

Пусть число – аbcd, тогда

а+b+ c+d=a·b·c·d

Так как аbcd

(10с+ d) и d - четное

Среди цифр a, b, с и d

Не может быть только одна единица, 1+b+c+d=b·c·d –равенство невозможно

Среди цифр a, b, с и d нет нулей иначе произведение равно 0

№ 6Найдите четырёхзначное число, кратное 4, сумма цифр которого равна их произведению

Среди цифр a, b, с и d

две единицы

Из 1 равенства с+4=2с, значит с=4

Рассмотрим двузначные числа кратные 4:

12;

16;

24

Из 2 равенства с+8=6с, с – дробное, чего быть не может

3-е равенство верное

1+с+1+2=1 ·с·1·2

1+с+1+6=1 ·с·1·6

Искомые числа: 4112, 1412, 1124

1+1+2+4=1 ·1·2·4

Приведите пример шестизначного натурального числа, которое записывается только цифрами 1 и 2 и делится на 72. В ответе укажите ровно одно такое число.

Число кратно 72, значит кратно 9 и кратно 4 и 8

Сумма цифр кратна 9, значит в записи должны быть три двойки и три единицы, т.к. 1+1+1+2+2+2=9 кратно 9

Число из двух последних цифр делится на 4 , значит это 12

Число из трех последних цифр делится на 8 , значит это 112

122112 – одно из чисел

1

1

2

1

2

2

В 19

х

3

х

1

0

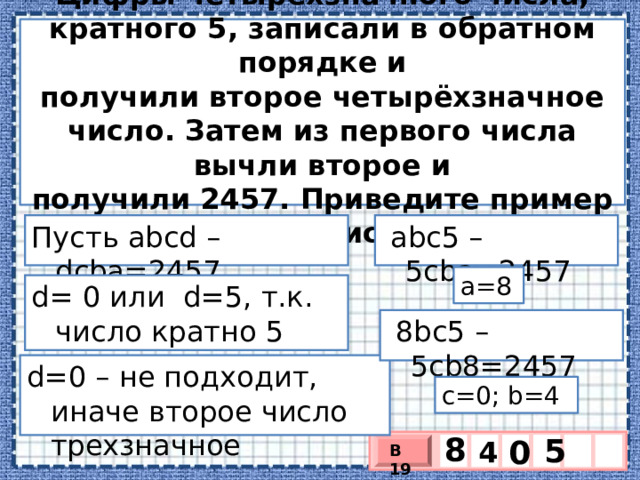
Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе четырёхзначное число. Затем из первого числа вычли второе и получили 2457. Приведите пример такого числа.

аbc5 – 5cba=2457

Пусть аbcd – dcba=2457

а=8

d= 0 или d=5, т.к. число кратно 5

8bc5 – 5cb8=2457

d=0 – не подходит, иначе второе число трехзначное

с=0; b=4

8

5

0

4

В 19

х

3

х

1

0

Вычеркните в числе 53164018 три цифры так, чтобы получившееся число делилось на 15. В ответе укажите ровно одно получившееся число.

Т.к. число кратно 15, то кратно 5 и 3, значит окачивается либо на 5, либо на 0, и сумма цифр кратна 3

Вычеркнем последние две цифры, тогда число оканчивается цифрой 0

5+3+1+6++4+0= 19 . Можно вычеркнуть либо 1, либо 4

5

6

3

0

4

0

х

В 19

3

х

1

0

Автор шаблона презентации:

Ермолаева И.А.

Название сайта: http://www.nsportal.ru/ermolaeva-irina-alekseevna Для шаблона использовались

http://lake.k12.fl.us/cms/cwp/view.asp?A=3&Q=427619