Численная реализация некоторых одномерных методов решения задач оптимизации

ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ

Тригонометрические задачи одна из самых сложных тем в школьном курсе математики. Тригонометрические уравнения возникают при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях.

Целью исследования данной работы является выполнение заданий на тождественные преобразования тригонометрических выражений, поскольку они встречаются в ЕГЭ как в качестве отдельных заданий, так и используются для решения тригонометрический уравнений и неравенств, а так же комбинированных заданий.

Проблема исследования состоит в рассмотрении теоретических основ темы «Преобразование тригонометрических выражений» и методики обучения решению таких типов задач.

Цель исследования: рассмотреть различные способы и методы решения тригонометрических выражений.

Выражение, в котором переменная содержится под знаками тригонометрических функций, называют тригонометрическим. Для преобразования выражений используют свойства тригонометрических функций и формулы тригонометрии.

Формулы сложения и вычитания аргументов. Для любых действительных чисел  и  справедливы формулы:

 (1)

 (2)

 (3)

 (4)

 (5)

 (6)

Формула (5) верна при  отличных от 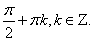 Формула (6) верна при отличных от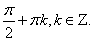 

Пример 1. Вычислить  

Решение. Имеем Воспользовавшись формулой (3) при  получим:  

Известно, что   . Значит  

Итак,  

Пример 2. Найти  если  

Решение. Воспользуемся формулой (5) и учтем, что  

Имеем 

Формулы приведения. Под формулами приведения обычно понимают формулы, сводящие значение тригонометрической функции аргумента вида  к функции аргумента  [12, с.342].

Пусть, например, нужно вычислить  Тогда имеем: .

Аналогично  

Подобным же образом выводятся и остальные формулы приведения, эти формулы даны в следующей таблице:

Таблица 1

Формулы приведения

Соотношения между тригонометрическими функциями одного и того же аргумента. Если в формуле (2) положить то получим:

 (6)

Откуда, в свою очередь, находим, что

 (7)

 (8)

Тождество (7) справедливо при  а тождество (8) — при  .

Равенства (6), (7), (8) связывают между собой различные тригонометрические функции одного и того же аргумента. Известны еще два равенства, связывающие между собой различные тригонометрические функции одного и того же аргумента. Это

 и  

Перемножая эти равенства, получаем равенство   справедливое при  

Формулы двойного угла. Если в формулах (3), (1), (5) положить  то получим следующие тождества [4, с.231]:

(9)

(10)

(11)

С помощью формул (9), (10) и (11) можно выразить синус, косинус, тангенс любого аргумента через тригонометрические функции вдвое меньшего аргумента. Например, справедливы следующие равенства:

В ряде случаев полезным оказывается использование полученных формул (справа налево), то есть замена выражения  выражением  (или выражения  выражением ), выражения  выражением  и, наконец, выражения  выражением  

Пример 3. Упростить выражение  

Решение.  

Литература:

1.                Асмолов, А.Г. Математика в школе / А.Г. Асмолов – М.: Просвещение, 2016.

2.                Блох, А.Я. Методика преподавания математики в средней школе: Частная методика: учеб. пособие для студентов пед. ин-тов по физ.-мат. спец. В.И.Мишин – М.: Просвещение, - 2017. – Гл. 5.

3.                Виленкин, Н.Я. Равенства, тождества, уравнения, неравенства / Н.Я. Виленкин – М.: Просвещение, – 2016. – 271 с.

4.                  Макарычев, Ю.Н. Алгебра: учеб. для 8 кл. общеобразоват. учреждений / С.А. Теляковский – М. : Просвещение, 2015. - 271 с.