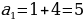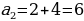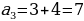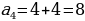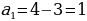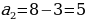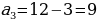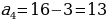| I. Организационный момент | Приветствие. Проверка готовности обучающихся к уроку. Создание в классе атмосферы психологического комфорта. – Я уверена, что, если мы будем работать вместе, у нас все получится! | Настраиваются на учебную деятельность. Концентрируют внимание на работе на уроке.
| Формирование навыков самоорганизации |
| II. Актуализация опорных знаний и жизненного опыта. Постановка учебной задачи | Предлагает обучающимся рассказать, что им известно о понятии «последовательность».
Вопрос запуска постановки учебной задачи: – Что вам известно о числовых последовательностях? Формулирует учебную задачу: – Изучить числовые последовательности | Выступают перед классом или в группах. – Я знаю… – Я слышал… – Нам рассказывали… – Я выполнял… Осознают важность решения поставленной учебной задачи | Развитие навыков целеполагания |
| III. Сообщение темы. Постановка цели и задач урока | Сообщает тему урока. Организует совместное с учащимися формулирование цели и задач урока. – Внимательно прочитайте тему урока. – Что от вас ожидается на уроке? – Какие цели и задачи вы можете перед собой поставить? | Записывают в тетрадь тему урока. Участвуют в формулировании целей и задач урока: – понять, что собой представляют числовые последовательности – научиться приводить примеры числовых последовательностей | Умение принимать и сохранять учебную задачу |
| IV. Мотивирование к учебной деятельности | Способствует обсуждению мотивационных вопросов. – Есть ли у меня желание узнавать что-то новое? – Что меня заинтересовало в теме урока? – При каких условиях урок будет для меня полезным? – Какова моя цель на данный урок? | Отвечают на мотивационные вопросы. Создают условия для успешной учебной деятельности. | Умение выражать свои мысли, демонстрировать самомотивацию |
| V. Создание ситуации затруднения. Работа над темой урока | Организует обсуждение проблемного вопроса: – С какими объектами удобней работать, если они пронумерованы? Организует поиск и анализ информации о понятиях «последовательность», «член последовательности», «n-й член последовательности», «числовая последовательность»
Предлагает проанализировать примеры числовых последовательностей.
Объясняет обучающимся, что последовательности бывают конечными и бесконечными. Для обозначения членов последовательности используют буквы с индексами: 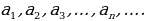 Индекс указывает порядковый номер члена последовательности. Индекс указывает порядковый номер члена последовательности. Последовательности можно задавать с помощью формул. Например, формула 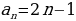 задает последовательность натуральных нечетных чисел: задает последовательность натуральных нечетных чисел: 1, 3, 5, 7, 9, … . Организует анализ информации.
Организует анализ решения задания. Отвечает на вопросы обучающихся. Задание. Последовательность 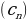 задана формулой n-го члена задана формулой n-го члена 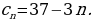 Является ли членом этой последовательности число: 1) 19; 2) Является ли членом этой последовательности число: 1) 19; 2) 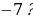 В случае утвердительного ответа укажите номер этого члена В случае утвердительного ответа укажите номер этого члена
| Принимают участие в обсуждении решения задачи. Выделяют объекты, которые удобно пронумеровать для работы с ними: дни недели, подъезды дома, квартиры дома, вагоны поезда и т.д. Осуществляют поисково-исследовательскую деятельность. Работают с разными источниками информации. | Объект исследования | Найденная информация | Вопросы для дополнительных исследований | | Последовательность | Объекты, которые пронумерованы подряд натуральными числами 1, 2, 3, …, n, …, образуют последовательности | Как…? | | Член последовательности | Объекты, образующие последовательности | Почему…? | | n-й член последовательности | Если член последовательности имеет номер n, то его называют n-м членом последовательности | Что…? | | Числовая последовательность | Если членами последовательности являются числа, то такую последовательность называют числовой | Каким образом…? | Анализируют примеры числовых последовательностей. | Пример последовательности | Название последовательности | Мне непонятно… | | 1, 2, 3, 4, 5, … | Последовательность натуральных чисел |
| | 2, 4, 6, 8, 10, … | Последовательность четных чисел |
| | 0,3; 0,33; 0,333; … | Последовательность десятичных приближений дроби 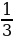 |
| | 19, 38, 57, 76, 95 | Последовательность двузначных чисел, кратных 19 |
| | –1, –2, –3, –4, –5, … | Последовательность отрицательных целых чисел |
| Делают записи в тетради. Задают вопросы учителю. Анализируют информацию. | Информация | Мне непонятно… | Вопросы учителю | | Формулу, выражающую член последовательности через один или несколько предыдущих членов, называют рекуррентной формулой | Каким образом…? | Зачем…? | | Условия, определяющие первый или несколько первых членов, называют начальными условиями | Что…? | Зачем…? | | Способ задания последовательности с помощью начальных условий и рекуррентной формулы называют рекуррентным способом задания последовательности | Почему…? | Как…? | Анализируют предложенное решение задания. Формулируют вопросы учителю для уточнения логики решения задания. | Решение | Комментарий ученика. Вопросы учителю | | 1) Если число 19 является членом данной последовательности, то существует такое натуральное значение n, при котором выполняется равенство 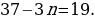 Отсюда Отсюда 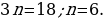 Следовательно, число 19 является шестым членом последовательности Следовательно, число 19 является шестым членом последовательности 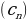
| Зачем…? | | 2) Имеем: 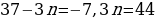 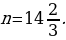 Так как число Так как число 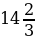 не является натуральным, то число не является натуральным, то число 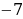 не является членом данной последовательности не является членом данной последовательности
| Каким образом…? | | Ответ: 1) является, 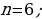 2) не является 2) не является | Как…? |
| Умение выражать свои мысли в соответствии с задачей.
Умение анализировать информацию
|
| VI. Закрепление изученного материала | Организует конкурс на составление лучшего вопроса по материалу, который был изучен на уроке
| Придумывают вопросы. Отвечают на вопросы одноклассников. Совместно с учителем определяют лучший вопрос. Примеры вопросов: – Почему не каждую последовательность можно назвать числовой? – Какие существуют способы задания последовательностей? | Умение осуществлять актуализацию полученных на уроке знаний и умений |
| VII. Решение заданий | Задания: 1. (№ 692) Запишите в порядке возрастания пять первых членов последовательности: 1) двузначных чисел, кратных числу 4; 2) неправильных обыкновенных дробей с числителем 11; 3) натуральных чисел, дающих при делении на 8 остаток 5. Укажите, конечными или бесконечными являются эти последовательности. 2. (№ 694) Найдите четыре первых члена последовательности 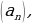 заданной формулой n-го члена: заданной формулой n-го члена: 1) 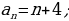
2) 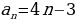 | Решения. 1.
1) 12, 16, 20, 24 28 – конечная последовательность. 2) 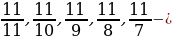 конечная последовательность. конечная последовательность.
3) 13, 21, 29, 37, 45 – конечная последовательность.
2.
1) 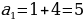 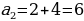 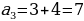 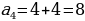 2) 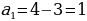 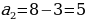 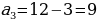 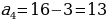 | Умение самостоятельно принимать решения |
| VIII. Подведение итогов урока. Рефлексия | Организует подведение итогов урока обучающимися. Способствует размышлению учащихся над вопросами. – Можно ли сказать, что я понимаю, что собой представляет числовая последовательность? – Есть ли у меня желание рассказать о числовых последовательностях своим друзьям? – Доволен ли я своей работой на уроке? – Получил ли я удовольствие от процесса познания нового? | Подводят итоги своей работы на уроке. Проводят самооценку, рефлексию. | Умение отслеживать цель учебной деятельности |







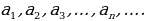 Индекс указывает порядковый номер члена последовательности.
Индекс указывает порядковый номер члена последовательности.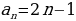 задает последовательность натуральных нечетных чисел:
задает последовательность натуральных нечетных чисел: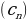 задана формулой n-го члена
задана формулой n-го члена 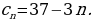 Является ли членом этой последовательности число: 1) 19; 2)
Является ли членом этой последовательности число: 1) 19; 2) 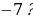 В случае утвердительного ответа укажите номер этого члена
В случае утвердительного ответа укажите номер этого члена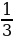
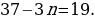 Отсюда
Отсюда 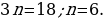 Следовательно, число 19 является шестым членом последовательности
Следовательно, число 19 является шестым членом последовательности 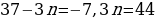
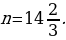 Так как число
Так как число 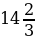 не является натуральным, то число
не является натуральным, то число 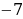 не является членом данной последовательности
не является членом данной последовательности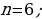 2) не является
2) не является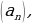 заданной формулой n-го члена:
заданной формулой n-го члена: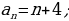
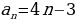
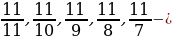 конечная последовательность.
конечная последовательность.