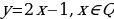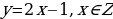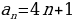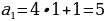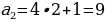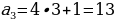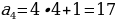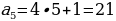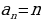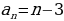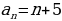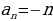Проект изучения темы «Числовые последовательности»
Выполнили: Бычков Александр, Вронская Наталья
Учебник: Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений/ А. Г. Мордкович, П. В. Семенов. – 12-е изд., стер. – М.: Мнемозина, 2010. – 224 с. Глава 4, § 15
-
Обзор математической и методической литературы
-
Глейзер Г. И. История математики в школе VII-VIII кл. Пособие для учителей. – М.: Просвещение, 1982. – 240 с.
В книге в виде коротких статей содержится материал из истории математики, доступный ученикам VII-VIII классов. Материал предназначен как для занятий на уроках, так и на внеклассных занятиях. В пособии также присутствует набор задач по арифметике, алгебре, геометрии известных математиков прошлых веков. Касательно данной темы, в книге даются очерки по тому, как развивалось понятие числовой последовательности на протяжении истории, приводятся примеры числовых последовательностей, известных в древности, а также рассказывается о частных видах – арифметической и геометрической прогрессии.
-
Медынский М. М. Полный курс элементарной математики в задачах и упражнениях. Книга 2: Числовые последовательности и прогрессии. М: Эдитус, 2015. – 208 с.
В книге изложены основные методы решения задач по разделу «Числовые последовательности и прогрессии». Дан необходимый теоретический материал, приведены примеры с решениями, задания, упражнения для самостоятельной работы.
-
Цыпкин А.Г., Пииский А.И. Справочник по методам решения задач по математике средней школы. – М.: Наука, 1989. – 576 с.
Книга содержит основные методы решения задач школьного курса математики, а также некоторые задачи, не входящие в существующую программу средней школы. Приводятся необходимые теоретические сведения. Изложение метода сопровождается разбором типичных задач. Приводятся задачи для самостоятельного решения. Глава 7 посвящена последовательностям, а именно в ней изложены: определение и свойства последовательности, предел последовательности, вычисление пределов последовательности.
-
Мордкович А. Г. Алгебра. 9 класс: методическое пособие для учителя/ А. Г. Мордкович, П. В. Семенов. – М.: Мнемозина, 2010. – 72 с.
В пособии представлено примерное планирование учебного материала в 9 классе, разъясняются важнейшие особенности учебника А. Г. Мордковича, П. С. Семенова «Алгебра-9». Пособие содержит также решение трудных задач из задачника «Алгебра-9». Касательно темы «Числовые последовательности» здесь авторы приводят некоторые рассуждения на мотивирование учащихся этой теме, изложение материала, обращается внимание на особенности решения некоторых задач, высказывается своя точка зрения касательно места этой темы вообще в школьном курсе математики.
-
Общая характеристика темы:
-
особенности и роль темы в математике (включая историческую справку) и в школьном курсе математики;
В настоящее время числовые последовательности рассматриваются как частные случаи функции. Числовая последовательность есть функция натурального аргумента.
Понятие числовой последовательности возникло и развивалось задолго до создания учения о функции. Вот примеры бесконечных числовых последовательностей, известных еще в древности:
-
1, 2, 3, 4, 5, … - последовательность натуральных чисел;
-
2, 4, 6, 8, 10, … – последовательность четных чисел;
-
1, 3, 5, 7, 9, … - последовательность нечетных чисел;
-
1, 4, 9, 16, 25, … - последовательность квадратов натуральных чисел;
-
2, 3, 5, 7, 11, … - последовательность простых чисел;
-
1, 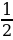 ,
, 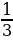 ,
, 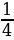 ,
, 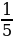 , … - последовательность чисел, обратных к натуральным.
, … - последовательность чисел, обратных к натуральным.
Число членов каждого из этих рядов бесконечно; первые пять последовательностей – монотонно возрастающие, последняя – монотонно убывающая. Все перечисленные последовательности, кроме 5, являются заданными ввиду того, что для каждой из них известен общий член, т. е. правило получения члена с любым номером. Для последовательности простых чисел общий член неизвестен, однако еще в III в. до н. э. александрийский ученый Эратосфен указал способ (правда, очень громоздкий) получения n-го ее члена. Этот способ был назван «решетом Эратосфена».
Идея предела последовательности восходит к V-IV вв. до н. э. Арифметическая и геометрическая прогрессии – частные виды числовых последовательностей – встречаются в памятниках II тысячелетия до н. э. в клинописных табличках как вавилонян, так и в египетских папирусах.
В Вавилоне, не имея в своем распоряжении ни современной символики, ни готовых формул, при решении задач на прогрессии были вынуждены придерживаться строго арифметических рассуждений. Египтяне же, видимо, пользовались правилом, которое можно записать в современной символике так:
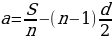 .
.
Оно эквивалентно нашей формуле:
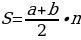
Происхождение этого правила не установлено: оно, вероятно, эмпирического характера.
Задачи на арифметические и геометрические прогрессии имеются и в древнекитайском трактате «Математики в девяти книгах, в котором нет, однако, указаний на применение какой-либо формулы суммирования.
Первые из дошедших до нас задач на прогрессии связаны с запросами хозяйственной жизни и общественной практики, как, например, распределение продуктов, деление наследства и т. д.
Вообще слово «прогрессия» латинского происхождения (progressio), буквально означает «движение вперед» (как и слово «прогресс) и встречается впервые у римского автора Боэция (V-VI в.в.). Первоначально под прогрессией понимали всякую числовую последовательность, построенную по закону, позволяющему неограниченно продолжать ее в одном направлении, например, последовательности натуральных чисел, их квадратов и кубов. В конце средних веков и в начале нового времени этот термин перестает быть общеупотребительным. В XVII в., например, Дж. Грегори употребляет вместо прогрессии термин «ряд», а другой видный английский математик Дж. Валлис, применяет для бесконечных рядов термин «бесконечные прогрессии».
Помимо прогрессий можно привести и другой вид числовой последовательности, также широко известный в математике. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Будучи рожденным в Пизе в богатой купеческой семье, он пришел в математику благодаря сугубо практической потребности установить деловые контакты. Числовой ряд, носящий сегодня его имя, вырос из проблемы с кроликами, которую Фибоначчи изложил в своей книге «Книга абака», написанной в 1202 году:
Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару?
Можно убедиться, что число пар в каждый из двенадцати последующих месяцев будет соответственно
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Иными словами, число пар кроликов создает ряд, каждый член в котором — сумма двух предыдущих. Он известен как ряд Фибоначчи, а сами числа — числа Фибоначчи. Легко видеть, что 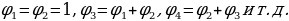 Другими словам, для чисел
Другими словам, для чисел  выполняется рекуррентное соотношение:
выполняется рекуррентное соотношение:
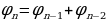 .
.
Однако можно указать формулу, позволяющую выразить 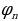 через n. Такая формула имеет вид:
через n. Такая формула имеет вид:
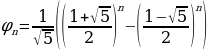 .
.
Это равенство называют формулой Бине по имени открывшего его (1843) французского математика Ж. Бине.
Оказывается, эта последовательность имеет множество интересных с точки зрения математики свойств. Вот пример: вы можете разделить линию на два сегмента, так что соотношение между большим и меньшим сегментом будет пропорционально соотношению между всей линией и большим сегментом. Этот коэффициент пропорциональности, приблизительно равный 1,618, известен как золотое сечение. В эпоху Возрождения считалось, что именно эта пропорция, соблюденная в архитектурных сооружениях, больше всего радует глаз.
Числа Фибоначчи часто встречаются в природе: интересно, что ими выражаются количества спиралей, по которым располагаются семечки в подсолнухе, цветочки в соцветиях ромашки, чешуйки в еловых шишках и др. Применяются они и в практической деятельности, например, при машинной сортировке и обработки информации. Используются числа Фибоначчи и в математике при генерировании случайных чисел, при нахождении экстремумов функции, производные которых неизвестны.
Тема «Числовые последовательности» входит в материал темы «Прогрессии», так как прогрессии - особый вид числовой последовательности. Тема «Последовательность» является одной из важных тем математики. В школьном курсе математики с помощью последовательностей «открываются» прогрессии. Возможно привлечение дополнительного материала.
При изучении числовых последовательностей в курсе школы тема «Последовательности» является вспомогательной и рассматривается лишь в объеме, необходимом для изучения арифметической и геометрической прогрессии. Однако тема «Последовательности» - это тема и математического анализа, поэтому некоторые начальные сведения, в будущем нужные ученику при изучении уже математического анализа, будут полезны и при изучении этой темы.
В реальной жизни мы часто встречаемся с различными видами последовательностей. Многие из них используются в самых различных науках. Например, числа Фибоначчи используются в хронологии и периодизации древнейшей истории, в архитектуре, искусстве, музыке, биологии, астрономии, при прогнозировании цен, определяют форму греческих ваз и спиральных галактик, строение подсолнуха и домика улитки. В «Справочнике по целочисленным последовательностям» Н. Слоуна собрано и упорядочено 2300 целочисленных последовательности, а значит и область их применения очень широка. Какую бы профессию не выбрал ученик в будущем, он обязательно встретится с каким-нибудь числовым рядом. Основной целью данного курса является демонстрация посредством последовательностей и их свойств возможностей математики при применении ее методов в физике, биологии, химии, экономике и других науках, а значит, и показать необходимость изучения математики для овладения любой профессией.
b. программа по математике: инвариантное содержание темы;
В 9 классе по базовому уровню данная тема представлена в разделе «Функции».
Рассматриваемые вопросы в рамках темы «Числовые последовательности»:
-
Числовые последовательности.
-
Способы задания числовых последовательностей.
-
Формула n-го члена.
-
Рекуррентная формула.
-
Числа Фиббоначи.
-
Возрастающие и убывающие (монотонные) последовательности
с. сравнительный анализ содержания темы в различных школьных учебниках
1) Мордкович А.Г. Алгебра и начала анализа. 10-11 В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень)/ А.Г. Мордкович, П.В. Семенов. – 6-е изд., стер. – М. Мнемозина, 2009. – 424 с.
Глава 4. Тригонометрические уравнения
В данном учебнике теме «Числовая последовательность» отводится первый параграф, который введен для возможности перехода к изучению прогрессий, как частных, но наиболее важных видов числовой последовательности. Автор учебника с самого начала посчитал важным показать учащимся, что такое числовая последовательность, как она связана с понятием функции и нужно ли изучать тему «Числовые последовательности» вообще. Поэтому приводятся многочисленные пояснения на эту тему. Изложение теоретического материала содержит многочисленные факты, в учебнике в полной мере раскрыты все без исключения понятия, приведены способы задания последовательностей, автор приводит многочисленные примеры, правда в изложении теоретического материала упущены такие понятия как конечные и бесконечные числовые последовательности. Тема в этом учебнике может с легкостью отдана на самостоятельный разбор.
2) Колягин Ю.М. Алгебра. 9 класс: учеб. для общеобразоват. организаций/[Ю.М. Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин].-М.: Просвещение, 2014.-304 с. Глава III. Прогрессии
Тема «Числовая последовательность» изучается в Главе III. Прогрессии, здесь ей также как и в учебнике Мордковича отводится самый первый параграф, позволяющий затем перейти к рассмотрению частных числовых последовательностей, как арифметическая и геометрическая прогрессия.
Изложение параграфа трудно назвать исчерпывающим. К сожалению, авторы так и не формулируют четко определения числовой последовательности. Учителю его придется формулировать самостоятельно, опираясь на текст, поясняющий смысл понятия «числовая последовательность». Упоминается понятие бесконечной числовой последовательности, однако почему-то ни слова не сказано про конечную числовую последовательность, а также нет примеров, иллюстрирующих существование таких последовательностей. Способы задания числовой последовательности не названы, в тексте их описания (очень скудные к слову) может найти лишь знакомый с данной темой, подготовленный человек. Словесный способ задания последовательности отсутствует вовсе. По данным, имеющимся в учебнике тяжело понять, в чем сущности данных способов, опять же почти нет наглядных примеров, иллюстрирующих все способы. Правда, авторы достаточно неплохо, лучше даже, чем у Мордковича, освещают вопрос о графическом представлении числовой последовательности. Ими приводятся даже не один, а целых два графических способа: с помощью точек на числовой прямой и с помощью точек на координатной плоскости. Материал касательно понятий возрастающей и убывающей последовательностей авторы решили не рассматривать вовсе. К очевидному достоинству данного учебника можно отнести исторические очерки, возникающие при изучении тем. В данной теме здесь очень хорошо рассказано про «Числа Фибоначчи».
2) Макарычев Ю.Н. Алгебра. 9 класс: учеб. для общеобразоват. организаций/[Ю.Н. Макарычев, Н.Г. Миндюк, К.И.Нешков, С.Б.Суворова]; под ред. С. А. Теляковского. – 21-е изд. - М.: Просвещение, 2014.-271 с. Глава IV. Арифметическая и геометрическая прогрессии
Как и в предыдущих рассмотренных учебниках, тема «Числовая последовательность» является начальным вспомогательным этапом для перехода к прогрессиям. Однако по стилю изложения данный учебник чем-то напоминает учебник Колягина Ю. М. и др. Изложение в нем ведется обрывочно, многие понятия, видимо, считаются ненужными и не присутствуют вообще. Определение числовой последовательности не выделено. Ученикам, читая данный учебник, будет тяжело понять, что же все-таки такое числовая последовательность, поскольку в параграфе расплывчато на примере поясняется смысл этого понятия. Способы задания числовой последовательности не выделены четко, как это сделано в учебнике Мордковича А. Г. Правда в отличие от учебника Колягина Ю. М. и др. в этом учебнике приводится достаточное количество примеров, поясняющих эти способы. Однако, приведенных способов лишь два: аналитический и рекуррентный. Про графический и словесный не сказано ни слова вообще. Авторы этого учебника тоже посчитали ненужным нагружать учеников такими понятиями как возрастающая и убывающая последовательности, выбросив их из своей теоретической справки.
Выводы: итак, проанализировав, приведенные выше три учебника, можно прийти к неутешительным выводам: инвариантное содержание темы «Числовые последовательности» раскрыто в достаточном объеме лишь в учебнике Мордковича А. Г. Именно в этом учебнике все необходимые понятия выделены четко, материал структурирован и носит законченный характер, понятия сопровождаются многочисленными пояснениями и примерами. При подготовке исследовательских проектов учитель смело может положиться на данный учебник, дав ученикам самим изучить и подготовить материал по данной теме. Остальные 2 учебника нуждаются в серьезной доработке, т. к. сами параграфы очень расплывчаты и характер даже приводимых понятий зачастую носит неопределенный характер. Необходимо также заметить, что все авторы анализируемых учебников видят необходимость изучения этой темы, как начального этапа, необходимого для введения темы «Арифметическая и геометрическая прогрессия». Касательно изложения материала по теме «Числа Фибоначчи», то здесь непременно хорошая подборка содержится в учебнике Колягина Ю. М.
-
Логико-дидактический анализ содержания темы:
Анализ теоретического материала
В теме присутствуют следующие дидактические единицы:
Первая дидактическая единица, которая приводится в пункте 1 учебника – это определение числовой последовательности:
Определение 1. Функцию  , называют функцией натурального аргумента или числовой последовательностью и обозначают
, называют функцией натурального аргумента или числовой последовательностью и обозначают 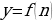 или
или 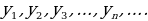
Оно дается через род и видовые отличия. Род – функция, видовые отличия: 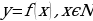 .
.
Следующие дидактические единицы – это определения первого, второго, третьего (и т. д.) членов последовательности:
Значения 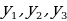 и т. д. называют соответственно первым, вторым, третьим (и т. д.) членами последовательности.
и т. д. называют соответственно первым, вторым, третьим (и т. д.) членами последовательности.
Определения также даются через род и видовые отличия. Родом здесь является значение, видовое отличие 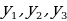 и т.д.
и т.д.
Приводится и определение индекса члена последовательности:
В символе  число
число 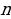 называют индексом, который задает порядковый номер того или иного члена последовательности.
называют индексом, который задает порядковый номер того или иного члена последовательности.
Определение индекса приводится через род и видовые отличия: род – число, видовое отличие: n в символе  , который задает порядковый номер того или иного члена последовательности.
, который задает порядковый номер того или иного члена последовательности.
В конце пункта 1 приводятся названия способов задания последовательности, которые в дальнейшем будут рассмотрены подробно:
-
аналитический;
-
словесный;
-
рекуррентный.
В начале пункта 2 автор дает определение аналитического задания последовательности, правда сформулированного некорректно:
Говорят, что последовательность задана аналитически, если указана формула ее n-го члена 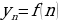 .
.
Можно сформулировать такое корректное определение:
Аналитическое задание последовательности – это способ задания последовательности, при котором указывается формула ее n-го члена 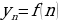 .
.
Тогда данное определение будет дано через род и видовые отличия:
род - способ задания последовательности, видовые отличия - при котором указывается формула ее n-го члена 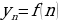 .
.
В примере 3 приводится определение стационарной последовательности:
Пример 3. 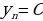 . Это значит, что речь идет о последовательности С, С, С, …, С, …, которую называют стационарной.
. Это значит, что речь идет о последовательности С, С, С, …, С, …, которую называют стационарной.
Определение дается через род и видовые отличия: род: последовательность, видовое отличие – вида 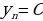 .
.
В пункте 3 говорится про словесное задание числовой последовательности. Оно пояснено лишь на примерах.
В пункте 4 приводится определение рекуррентного задания последовательности не в сформулированном виде:
Важный для приложений способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-ый член последовательности, если известны ее предыдущие члены. При вычислении членов последовательности по этому правилу мы как бы все время возвращаемся назад, выясняем, чему равны предыдущие члены. Такой способ задания последовательности называется реккурентым (от лат. recurrere – возвращаться). Чаще всего в таких случаях указывают формулу, позволяющую выразить n-ый член последовательности через предыдущие, и задают один-два начальных члена последовательности.
Однако его можно сформулировать через род и видовые отличия:
Рекуррентное задание последовательности – это способ задания последовательности, позволяющий указать формулу, выражающую n-ый член последовательности через предыдущие с заданием 1-2 начальных членов этой последовательности.
Здесь род - способ задания последовательности, видовые отличия - позволяющий указать формулу, выражающую n-ый член последовательности через предыдущие с заданием 1-2 начальных членов этой последовательности.
Пример 13 иллюстрирует определение последовательности Фибоначчи.

Определение дается через род и видовые отличия: род - последовательность, видовые отличие – где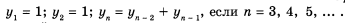
В пункте 5 приводятся определение возрастающей последовательности через род и видовые отличия:
Определение 2. Последовательность 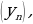 называется возрастающей, если каждый ее член (кроме первого) больше предыдущего:
называется возрастающей, если каждый ее член (кроме первого) больше предыдущего:
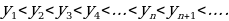
Род – последовательность, видовые отличия – 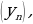 если каждый ее член (кроме первого) больше предыдущего:
если каждый ее член (кроме первого) больше предыдущего:
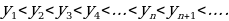
Приводятся определение убывающей последовательности через род и видовые отличия:
Определение 3. Последовательность 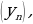 называют убывающей, если каждый ее член (кроме первого) больше предыдущего:
называют убывающей, если каждый ее член (кроме первого) больше предыдущего:
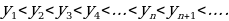
Род – последовательность, видовые отличия – 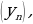 если каждый ее член (кроме первого) больше предыдущего:
если каждый ее член (кроме первого) больше предыдущего:
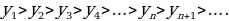
Приводится определение монотонных последовательностей:
Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.
Род – последовательности, видовые отличия – возрастающие и убывающие.
В конце пункта 5 приводятся две теоремы в условной форме (без доказательства):
Если 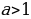 , то последовательность
, то последовательность 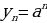 возрастает.
возрастает.
Если 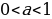 , то последовательность
, то последовательность 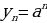 убывает.
убывает.
Выводы по анализу теоретического материала:
Понятие числовой последовательности несколько необычно для учащихся, т. к. с понятием функции хоть они уже хорошо и знакомы, к этому времени успели изучить много различных ее видов, но о функциях, определенных на области определения натуральных чисел, речи еще не было. Поэтому необходимо четко показать ученикам, что числовая последовательность – это не какое-то особое сконструированное понятие в математике, а лишь частный, особый случай функции на специфической области определения – множестве натуральных чисел.
В теоретическом материале темы четко выделяются 3 основные части:
-
понятие числовой последовательности, способы задания числовой последовательности: аналитический, словесный и рекуррентный;
-
различные примеры числовых последовательностей (особенно выделяется числовая последовательность, получившая название числа Фибоначчи);
-
понятия возрастающих и убывающих (монотонных) последовательностей.
Данный материал хорош для того, чтобы вместо проведения обычного урока изучения нового организовать для учеников урок-семинар изучения нового, на котором они бы полно смогли представить данную тему.
Перед докладом о понятии числовой последовательности неплохо было бы дать доклад на повторение основных понятий функции: само понятие функции, область определения и множество значений функции, способы задания функции и понятия возрастающих и убывающих функций.
При объяснении понятия числовая последовательность необходимы примеры числовых последовательностей, возникающих в жизни, человеческой практики, поясняющие необходимость изучения нового понятия, а также раскрывающие его как функции от натурального аргумента. Необходимо показать, как выглядит график таких функций – отдельные точки при соответствующих натуральных абсциссах в системе координат. Напоследок рассказать об особых числовых последовательностях – монотонных, сформулировать отдельно определения для возрастающих и убывающих последовательностях, а затем через эти два понятия ввести и понятие монотонной последовательности.
Уделяя внимание способам задания числовых последовательностей необходимо показывать возможность записи одной и той же числовой последовательности разными способами, вырабатывать умение переходить от одного способа к другому. При аналитическом способе задания учащиеся должны уметь находить любой член последовательности по его номеру и наоборот найти нужный номер члена, если он дан сам; при рекуррентном способе находить несколько членов последовательности через предыдущие. Нужно подчеркнуть достоинства и недостатки каждого из способов задания.
В отдельном докладе про числа Фибоначчи необходимо сообщить благодаря кому, и каким именно образом стала рассматриваться эта последовательность чисел, рассказать о способах записи чисел Фибоначчи и показать необходимость их отдельного изучения на примерах, где они возникают, например, при изучении «золотого сечения».
Анализ задачного материала
В задачном материале можно выделить:
-
Номера на отработку определения числовой последовательности:
№ 15.1-15.4
-
Задачи на отработку определения индекса члена последовательности (порядок следования, расположения между другими членами последовательности):
№ 15.10, 15.11
3) Упражнения на нахождение значений членов последовательности:
а) заданной словесно: № 15.6, 15.7, 15.8, 15.9, 15.24
б) заданной аналитически: № 15.12-15.14, 15.25-15.27
в) заданной рекуррентно: № 15.20, 15.21
4) Обратные задачи к задачам в пункте 3: нахождение номера по значению членов последовательности:
№ 15.18, 15.19, 15.35, 15.36
5) Задачи на задание числовой последовательности
а) аналитически: пример 1-10, № 15.5(а), 15.15-15.17, 15.28-15.29, 15.37
б) рекуррентно: пример 11-13, № 15.5 (в), 15.30, 15.32
в) словесно: № 15.5 (б), 15.33
6) Задачи на доказательство монотонности последовательностей:
пример 14-18, № 15.22, 15.23, 15.41, 15.42
-
Задачи на нахождение номера, начиная с которого все члены будут больше (меньше) заданного числа:
№ 15.39, 15.40
-
В задачном материале особо выделена ключевая задача на нахождение суммы первых n членов числовой последовательности, заданных словесно. В ней рассказывается специфический прием нахождения такой суммы. Это задача № 15.34
-
Здесь же представлена и задача на построение графика числовой последовательности: № 15.38
Выводы по анализу задачного материала:
В теме отрабатываются все дидактические единицы, но хотелось бы сделать некоторые дополнения. В задачнике Мордковича А. Г. приводятся разнообразные системы упражнений на задание числовой последовательности разными способами, но было бы неплохо добавить такое задание: перейти от рекуррентного способа задания к аналитическому, от аналитического к рекуррентному, т. к. в задачном материале присутствует лишь задачи на переход от словесного к аналитическому, либо рекуррентному. Хорошо отрабатываются понятие числовой последовательности, нахождение значений членов последовательности, заданных разными способами и наоборот нахождение индекса члена последовательности, однако нет номеров на графический способ задания числовой последовательности. Необходимо добавить такие задания: 1) дана числовая последовательность, заданная графически, найти первый, третий и другие ее члены; 2) дана числовая последовательность, заданная графически, найти номера членов, которые равны соответственно некоторым числам. Задачи на доказательство монотонности последовательности представлены хорошо. В целом же задачный материал все же можно назвать исчерпывающим и полным по данной теме. Сами же задания по данной теме прозрачны и не должны вызывать особых затруднений у учащихся. Можно даже выработать правила по некоторым типам заданий. Например, для нахождения номера последовательности, заданной аналитически, нужно подставить вместо обозначения n-го члена в формуле наше значение и решить получившееся уравнение, отобрать среди корней лишь те значения, которые являются натуральными.
-
Постановка учебных задач, диагностируемых целей.
Учебная задача урока: В результате докладов учащихся познакомить с исторической справкой возникновения понятия числовой последовательности, рассказать о её применении, рассмотреть определение числовой последовательности, способов ее задания, а также привести примеры простейших числовых последовательностей, известных в математике.
Диагностируемые цели урока: В результате урока ученик:
знает:
- историческую справку возникновения числовых последовательностей;
- применение числовых последовательностей в окружающем мире;
- определение числовой последовательности, индекса, возрастающей, убывающей числовой последовательности;
- обозначение числовой последовательности;
- способы задания числовой последовательности: аналитический, словесный, рекуррентный;
- свойства монотонных числовых последовательностей.
умеет:
- приводить примеры числовой последовательности из окружающего мира;
- определять способ задания числовой последовательности;
- переходить от одного способа задания числовой последовательности к другому;
- задавать числовую последовательность разными способами;
- находить члены последовательности, если известен способ задания последовательности.
понимает:
- практическую значимость данной темы;
- что числовая последовательность – частный случай функции (функция от натурального аргумента).
-
Тематическое планирование
| № | Тема урока | Тип урока | Учебная задача урока | Методы обучения |
| 1. | Числовая последовательность | Урок – семинар изучения нового | В результате докладов учащихся познакомить с исторической справкой возникновения понятия числовой последовательности, рассказать о её применении, рассмотреть определение числовой последовательности, способов ее задания, а также привести примеры простейших числовых последовательностей, известных в математике. | Исследовательский, репродуктивный, УДЕ |
| 2. | Числовая последовательность | Урок усвоения теории | Провести опрос по теории на тему Числовая последовательность, различные способы задания числовой последовательности» и на примере простейших задач показать ее применение. | Репродуктивный, частивно-поисковые, УДЕ |
| 3. | Числовая последовательность | Урок решения задач | Рассмотреть виды задач на различное задание числовой последовательности и на ее свойства. | Репродуктивный, частично-поисковые, УДЕ |
-
Подробный конспект урока
Характеристика урока
Учебник: Мордкович А.Г. Алгебра. 9 кл. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений/А. Г. Мордкович, П. В. Семенов. – 12-е изд., стер. – М.: Мнемозина, 2010. – 224 с., Г. 4, § 15. Числовые последовательности
Задачник: Мордкович А.Г. Алгебра. 9 кл. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений/[А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.]; под редакцией А. Г. Мордковича. – 12-е изд., испр. – М.: Мнемозина, 2010. – 223 с., Г. 4, § 15. Числовые последовательности
Тема: Числовые последовательности.
Тип урока: урок-семинар изучения нового.
Учебная задача урока: В результате докладов учащихся познакомить с исторической справкой возникновения понятия числовой последовательности, рассказать о её применении, рассмотреть определение числовой последовательности, способов ее задания, а также привести примеры простейших числовых последовательностей, известных в математике.
Диагностируемые цели урока: В результате урока ученик:
знает:
- историческую справку возникновения числовых последовательностей;
- применение числовых последовательностей в окружающем мире;
- определение числовой последовательности, индекса, возрастающей, убывающей числовой последовательности;
- обозначение числовой последовательности;
- способы задания числовой последовательности: аналитический, словесный, рекуррентный;
- свойства монотонных числовых последовательностей.
умеет:
- приводить примеры числовой последовательности из окружающего мира;
- определять способ задания числовой последовательности;
- переходить от одного способа задания числовой последовательности к другому;
- задавать числовую последовательность разными способами;
- находить члены последовательности, если известен способ задания последовательности.
понимает:
- практическую значимость данной темы;
- что числовая последовательность – частный случай функции (функция от натурального аргумента).
Учебные действия, формируемые на уроке:
-
Личностные: умение учащегося устанавливать связи между целью учебной деятельности и её мотивом, т.е. между результатом учения, и тем, что побуждает деятельность, ради чего она осуществляется, таким образом, должна осуществляться осмысленная организация собственной деятельности ученика
-
Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что ещё неизвестно, планирование - определение последовательности промежуточных целей с учётом конечного результата, оценка - выделение и осознание учащимся того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения
-
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, т. е. определение цели сотрудничества, функций участников, способов взаимодействия, умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка, умение доказывать собственное мнение
-
Познавательные: анализ объектов с целью выделения признаков (существенных, несущественных);выдвижение гипотез и их обоснование; построение логической цепи рассуждений, доказательство; подведение под понятие; выведение следствий; установление причинно-следственных связей.
Методы обучения: исследовательский, частично-поисковые, УДЕ.
Форма работы: фронтальная, групповая.
Средства обучения: традиционные, презентация.
Структура урока:
Мотивационно-ориентировочная часть (2 минут)
Операционно-познавательная часть (40 минут)
Рефлексивно-оценочная часть (3 минут)
За две недели до изучения темы «Числовые последовательности» учитель дает ученикам предваряющее домашнее задание: разбившись на группы по 6 человек, они должны выбрать одну из приведенных ниже тем, подготовить реферат по ней, а затем на уроке представить тезисно с презентацией свой доклад. Кроме того в каждой группе должно быть выделено 2 ученика: докладчик и оппонент. Цель докладчика рассказать свое выступление по теме, которую выбрала группа, оппонент после выступления должен задать 1-2 вопроса. Ученики в течении этих двух недель должны представить свои предварительные выступления, учитель выслушивает, корректирует, исправляет их. До начала урока на доске вывешивается план семинара. На выступление каждого доклада дается не более 10 минут.
Темы докладов:
-
Основные понятия темы «Функция».
Список литературы:
-
Алгебра. 7 класс: учеб. для общеобразоват. учреждений/ [Ю.М. Колягин, М. В. Ткачева, Н. Е. Федорова, М.И. Шабунин]. – М.: Просвещение, 2012. – 319 с.
-
Алгебра. 9 класс: учеб. для общеобразоват. организаций/ [Ю.М. Колягин, М. В. Ткачева, Н. Е. Федорова, М.И. Шабунин]. – М.: Просвещение, 2014. – 304 с.
-
История возникновения и применения числовой последовательности. Основные понятия, связанные с числовой последовательностью.
Список литературы:
-
Глейзер Г. И. История математики в школе VII-VIII кл. Пособие для учителей. – М.: Просвещение, 1982. – 240 с.
-
Мордкович А.Г. Алгебра. 9 кл. В 2 ч. Ч. 1. Учеб. для учащ. общеобр. уч. – М.: Мнемозина, 2010, Г. 4, § 15
-
Алгебра. 9 класс: учеб. для общеобразоват. организаций/ [Ю.М. Колягин, М. В. Ткачева, Н. Е. Федорова, М.И. Шабунин]. – М.: Просвещение, 2014. – 304 с.
-
Способы задания числовой последовательности.
Список литературы:
-
Мордкович А.Г. Алгебра. 9 кл. В 2 ч. Ч. 1. Учеб. для учащ. общеобр. уч. – М.: Мнемозина, 2010, Г. 4, § 15
-
М. М. Медынский «Полный курс элементарной математики в задачах и упражнениях. Книга 2: Числовые последовательности и прогрессии. М.: Эдитус, 2015. – 208 с.
-
Числа Фибоначчи.
Список литературы:
-
Н.М.Воробьёв, Числа Фибоначчи, Москва, Наука, 1992, 144 с.
-
Шибасов Л. Фибоначчиевы кролики/Шибасов Л., Шибасова З.// Квант. – 2005. - № 2. – с. 7-9.
-
Алгебра. 9 класс: учеб. для общеобразоват. организаций/ [Ю.М. Колягин, М. В. Ткачева, Н. Е. Федорова, М.И. Шабунин]. – М.: Просвещение, 2014. – 304 с.
Ход урока
Мотивационно-ориентировочная часть
Мотивация
- Ребята, задолго до этого на дом вам предлагалось разбиться на группы, и каждой группе нужно было подготовить доклад на свою конкретную тему по теме «Числовые последовательности».
Постановка учебной задачи:
- Поэтому целью нашего сегодняшнего урока станет изучение понятия «Числовая последовательность».
Планирование решения учебной задачи:
- Мы с ваши заслушаем подготовленные вами доклады и затем кратко запишем в тетрадях основные положения из них.
Операционно-познавательная часть
- Итак, тема нашего урока: Числовые последовательности.
- Ранее мы уже с вами изучали основное понятие в математике – понятие функции. Как вы сегодня убедитесь, оно будет очень значимо для нас. Поэтому давайте прежде вспомним основные понятия, связанные с функцией.
Выступает 1 группа с докладом:
Основные понятия темы «Функция».
Докладчик:
- Вспомним для начала, что такое функция:
Определение. Функцией называется закон 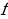 , по которому каждому элементу
, по которому каждому элементу  ставится в соответствие единственный элемент
ставится в соответствие единственный элемент 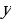 . При этом
. При этом 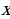 называют независимой переменной (аргументом), а
называют независимой переменной (аргументом), а 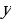 - зависимой переменной (функцией).
- зависимой переменной (функцией).
Учащиеся записывают определение функции в тетрадь.
Можно привести многочисленные примеры функций. Вот некоторые из них:
-
зависимость между стороной квадрата а и его площадью 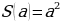
-
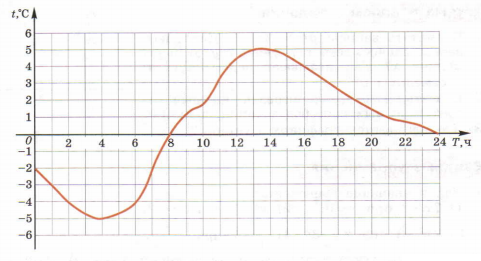
зависимость времени и температуры воздуха, наблюдавшейся в течение этого времени
Множество всех допустимых значений аргумента 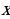 называется областью определения функции и обозначается
называется областью определения функции и обозначается 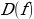 .
.
Множество всех значений, которые принимает зависимая переменная, называют множеством значений функции и обозначается 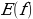 .
.
Ученики пишут определение области определения и множество значений функции.
Примеры:
-

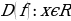
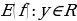
-
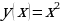
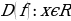
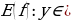
3)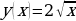
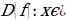
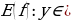
Функция, как известно, может быть задана несколькими способами:
-
Аналитический способ
Данный способ подразумевает задание формулы, позволяющей вычислить любое у, придавая различные значения x из X в этой формуле.
Пример. Зависимость стороны квадрата 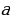 от его периметра P можно задать формулой:
от его периметра P можно задать формулой: 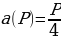
-
Табличный способ
Заключается в задании отдельных значений аргумента и соответствующих им значений функции. Данный способ не позволяет узнать, как ведёт себя функция за пределами таблицы, не хватает наглядности.
Пример:
Функцию 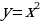 , заданную аналитически, можно представить в виде таблицы так:
, заданную аналитически, можно представить в виде таблицы так:
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| 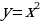
| 4 | 1 | 0 | 1 | 4 | 9 | 16 |
-
График
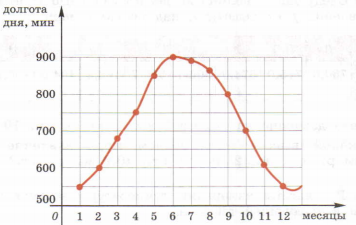
Для наглядного представления функциональной зависимости, используются специальные рисунки, называемые графиками. Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям независимой переменной, а ординаты - соответствующим значениям функции.
Пример. Зависимость долготы дня от времени года можно представить в следующем виде:
Ученики зарисовывают в тетрадь краткую схему, иллюстрирующую все 3 способа:
С
 пособы задания функции
пособы задания функции
Аналитический Табличный График
Напомним теперь, какая функция называется возрастающей, убывающей.
Определение. Функция 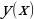 называется возрастающей на некотором промежутке, если для любых
называется возрастающей на некотором промежутке, если для любых 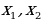 , принадлежащих данному промежутку, таких, что
, принадлежащих данному промежутку, таких, что 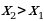 , выполняется неравенство
, выполняется неравенство 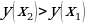 .
.
Примеры:
-
Функция 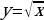 возрастает при
возрастает при 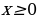
-
Функция 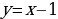 возрастает при
возрастает при 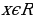
Определение. Функция 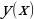 называется убывающей на некотором промежутке, если для любых
называется убывающей на некотором промежутке, если для любых 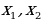 , принадлежащих данному промежутку, таких, что
, принадлежащих данному промежутку, таких, что 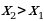 , выполняется неравенство
, выполняется неравенство 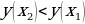 .
.
Примеры:
-
Функция 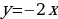 убывает при
убывает при 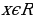
-
Функция 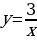 убывает при
убывает при 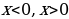
Ученики кратко записывают определения возрастающей и убывающей функции:
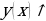 , если
, если 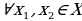
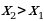
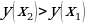
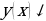 , если
, если 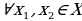
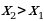
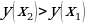
Вопросы оппонента:
-
Будут ли функциями следующие соответствия?
а) 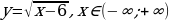
б) 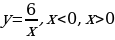
в) 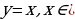
г) 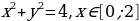
-
Найти область определения и множество значений функций:
а) 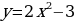
б) 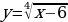
Ответы докладчика:
-
а) Не будет, т.к. не для каждого 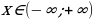 ставится в соответствие
ставится в соответствие  .
.
б) Будет, т. к. каждому элементу 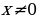 ставится в соответствие единственный элемент
ставится в соответствие единственный элемент 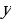 .
.
в) Будет, т. к. каждому элементу 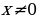 ставится в соответствие единственный элемент
ставится в соответствие единственный элемент 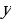 .
.
г) Не будет, т. к. некоторым 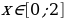 ставится в соответствие не единственный
ставится в соответствие не единственный 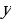 .
.
2) а) 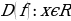
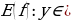
б) 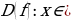
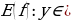
Выступает 2 группа с докладом:
История возникновения и применения числовой последовательности. Основные понятия, связанные с числовой последовательностью.
Докладчик:
- В повседневной практике часто используется нумерация различных предметов, чтобы указать порядок их расположения. Например, дома на каждой улице нумеруются. В библиотеке нумеруются читательские абонементы и затем располагаются в порядке присвоенных номеров в специальных карточках. Иными словами, читательские абонементы располагают в определенной последовательности.
Можно привести и такой пример:
На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля будет на складе через 1 день, 2 дня, 3 дня и т. д.?
Если за х принять число дней, а за у – количество угля (в тоннах), то математической моделью ситуации будет линейная функция, заданная на множестве N натуральных чисел:
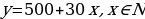 .
.
В результате мы получим следующую числовую последовательность:
530, 560, 590, …
Итак, уже здесь прослеживается функциональная зависимость количества угля от пройденных дней. Следовательно, перед нами функция, правда, определенная на специфическом множестве – множестве натуральных чисел. Поэтому вполне логично дать такое определение числовой последовательности:
Определение 1. Функцию 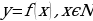 , называют функцией натурального аргумента или числовой последовательностью и обозначают
, называют функцией натурального аргумента или числовой последовательностью и обозначают 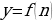 или
или 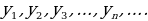
Учащиеся записывают определение числовой последовательности в тетрадь.
Итак, подчеркнем еще раз:
Область определения числовой последовательности: множество натуральных чисел.
Множество значений может быть какое угодно.
А бывают ли нечисловые последовательности? Оказывается, да. Очередь в магазине, книги, расставленные на книжной полке и т. д. – вот примеры нечисловых последовательностей.
Однако мы будем рассматривать лишь числовые последовательности.
Значения 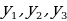 (и т.д.) называют соответственно первым, вторым, третьим (и т. д.) членами последовательности. В символе
(и т.д.) называют соответственно первым, вторым, третьим (и т. д.) членами последовательности. В символе  число n называют индексом, который характеризует порядковый номер того или иного члена последовательности (в записи
число n называют индексом, который характеризует порядковый номер того или иного члена последовательности (в записи 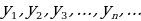 ).
).
Многоточия в обозначении последовательности (имеется в виду запись 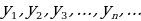 ) означают, что правее
) означают, что правее  располагаются дальнейшие члены последовательности (у4, у5, у6 и т.д.), рядом с уn находятся (а в случае необходимости и записываются)
располагаются дальнейшие члены последовательности (у4, у5, у6 и т.д.), рядом с уn находятся (а в случае необходимости и записываются) 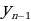 (слева) и
(слева) и 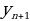 (справа). Члену
(справа). Члену 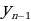 предшествует
предшествует 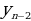 , а за
, а за 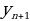 следует
следует 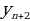 и т.д.
и т.д.
Для обозначения членов последовательности могут использоваться различные буквы, например: 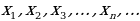 , или
, или 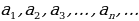 , или
, или 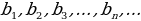 и т.д.
и т.д.
Последовательность, состоящая из конечного числа членов, называется конечной, а последовательность, состоящая из бесконечного числа членов, — бесконечной последовательностью.
Примеры конечных последовательностей:
-
Последовательность двухзначных чисел: 10, 11, 12, …, 99.
-
Последовательность однозначных четных чисел: 2, 4, 6, 8.
Примеры бесконечных последовательностей:
-
Последовательность степеней 2: 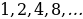 .
.
-
Последовательность четных чисел: 2, 4, 6, 8, … .
В математике существенный интерес представляют бесконечные числовые последовательности.
Учащиеся зарисовывают следующую схематичную схему:
Ч
 исловые последовательности
исловые последовательности
Конечные Бесконечные
2, 4, 6, 8 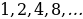
Сегодня числовые последовательности рассматриваются как частные случаи функции. Однако так было не всегда. Понятие числовой последовательности возникло и развивалось задолго до создания учения о функции. Вот примеры бесконечных числовых последовательностей, известных еще в древности:
-
1, 2, 3, 4, 5, … – последовательность натуральных чисел;
-
2, 4, 6, 8, 10, … – последовательность четных чисел;
-
1, 3, 5, 7, 9, … – последовательность нечетных чисел;
-
1, 4, 9, 16, 25, … – последовательность квадратов натуральных чисел;
-
2, 3, 5, 7, 11, …и – последовательность простых чисел;
-
1, 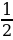 ,
, 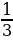 ,
, 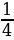 ,
, 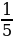 , … – последовательность чисел, обратных к натуральным.
, … – последовательность чисел, обратных к натуральным.
Число членов каждого из этих рядов бесконечно. Все перечисленные последовательности, кроме 5, являются заданными ввиду того, что для каждой из них известен общий член, т. е. правило получения члена с любым номером. Для последовательности простых чисел общий член неизвестен, однако еще в III в. до н. э. александрийский ученый Эратосфен указал способ (правда, очень громоздкий) получения n-го ее члена. Этот способ был назван «решетом Эратосфена».
Т. к. числовая последовательность – частный случай числовой функции, то у нее, как и у любой функции есть свойства. Ограничимся пока лишь свойством монотонности. Но вначале скажем, что такое монотонность. Введем два вспомогательных определения:
Определение 2. Последовательность 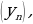 называется возрастающей, если каждый ее член (кроме первого) больше предыдущего:
называется возрастающей, если каждый ее член (кроме первого) больше предыдущего:
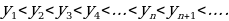
Ученики записывают кратко это определение так:
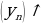 , если
, если 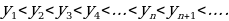
Пример 1:
Последовательность нечетных чисел: 1, 3, 5, 7, ..., 2n- 1, ... .
Действительно,
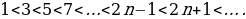
Определение 3. Последовательность 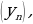 называют убывающей, если каждый ее член (кроме первого) больше предыдущего:
называют убывающей, если каждый ее член (кроме первого) больше предыдущего:
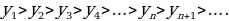
Ученики записывают кратко это определение так:
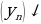 , если
, если 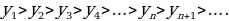
Пример 2:
Последовательность чисел, обратных к натуральным: 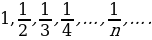
Действительно,
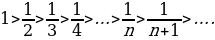
Тогда мы можем дать такое определение монотонной последовательности:
Определение 4. Возрастающие и убывающие последовательности образуют монотонную последовательность.
У чащиеся схематично это пишут в тетради так:
чащиеся схематично это пишут в тетради так:
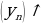
Монотонная последовательность
, если
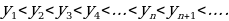
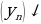 , если
, если 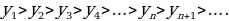
Примеры 1-2 иллюстрируют понятие монотонной последовательности.
Пример 3. 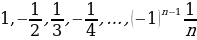 . Данная последовательность не является ни возрастающей, ни убывающей, т. к. в ней чередуются положительные и отрицательные числа. Поэтому данная последовательность не будет монотонной.
. Данная последовательность не является ни возрастающей, ни убывающей, т. к. в ней чередуются положительные и отрицательные числа. Поэтому данная последовательность не будет монотонной.
Оказывается, можно указать и признаки, позволяющие утверждать о возрастании или убывании некоторых последовательностей.
-
Если 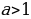 , то последовательность
, то последовательность 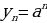 возрастает.
возрастает.
-
Если 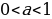 , то последовательность
, то последовательность 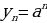 убывает.
убывает.
Примеры:
-
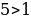 , тогда последовательность
, тогда последовательность 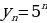 возрастает.
возрастает.
5, 10, 15, … .
-
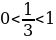 , тогда последовательность
, тогда последовательность 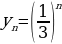 убывает.
убывает.
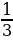 ,
, 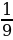 ,
, 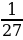 , … .
, … .
Вопросы оппонента:
-
Какие из предложенных функций являются числовыми последовательностями?
а) 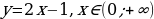
б) 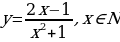
в) 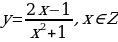
г) 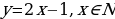
-
Определить возрастает или убывает следующая последовательность:
а) 1, 4, 9, 16, 25, …
б) 
Ответы докладчика:
-
Под б, г, т. к. эти функции являются функциями натурального аргумента.
-
Под а последовательность возрастает, т.к. 1
Под б последовательность убывает, т. к. 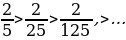
Выступает 3 группа с докладом:
Способы задания числовой последовательности.
Докладчик:
- Как и функции, числовые последовательности можно задать четырьмя основными способами: аналитически, рекуррентно, словесно и графически. Рассмотрим отдельно каждый из них.
Данный способ подразумевает задание формулы, позволяющей вычислить любой член последовательности по его номеру n. Сама формула при этом называется формулой общего члена последовательности.
Примеры:
-
Последовательность квадратов натуральных чисел задает формула: 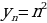 . Действительно, при
. Действительно, при
n = 1 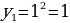
n = 2 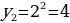
n = 3 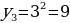
……..
-
Последовательность, состоящую из одного и того же числа: С, С, С, С, … , можно задать при помощи формулы 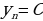 . Такая последовательность получила особое название – стационарная.
. Такая последовательность получила особое название – стационарная.
-
Последовательность нечетных чисел: 1, 3, 5, 7, 9, ... , задается при помощи формулы 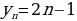 .
.
Действительно, при
n = 1 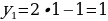
n = 2 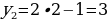
n = 3 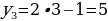
……..
Ученики постепенно начинают рисовать схему:
С пособы задания числовой последовательности
пособы задания числовой последовательности
Аналитический
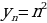
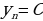
Важный для приложений способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-ый член последовательности, если известны ее предыдущие члены. При вычислении членов последовательности по этому правилу мы как бы все время возвращаемся назад, выясняем, чему равны предыдущие члены. Такой способ задания последовательности называется рекуррентым (от лат. recurrere – возвращаться). Чаще всего в таких случаях указывают формулу, позволяющую выразить n-ый член последовательности через предыдущие, и задают один-два начальных члена последовательности.
-
Последовательность четных чисел: 2, 4, 6, 8, 10, ... , задается при помощи рекуррентного соотношения 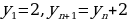 .
.
n = 1 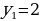
n = 2 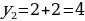
n = 3 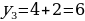
……..
-
Последовательность степеней 3: 1, 3, 9, 27, 81, 243, ... , задается при помощи рекуррентного соотношения  .
.
n = 1 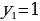
n = 2 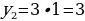
n = 3 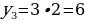
……..
Ученики продолжают заполнять схему:
С
 пособы задания числовой последовательности
пособы задания числовой последовательности
Аналитический Рекуррентный
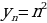
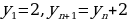
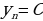

В некоторых случаях для последовательности чисел не удается указать ни формулы общего члена последовательности, ни рекуррентного способа вычисления ее членов. В таких случаях последовательность задается описанием способа получения ее членов.
Примеры:
-
Последовательность 2, 3, 5, 7, 11, … простых чисел состоит из натуральных чисел, делящихся только на 1 и на себя.
-
Последовательность 3,1; 3,14; 3,142; 3,1416; 3,14159; … состоит из приближенных значений числа  с точностью до 0,1; 0,01; 0,001 и т. д.
с точностью до 0,1; 0,01; 0,001 и т. д.
Ученики продолжают заполнять схему:
С
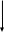
 пособы задания числовой последовательности
пособы задания числовой последовательности
Аналитический Рекуррентный Описательный
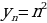
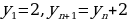 последовательность
последовательность
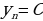
 простых чисел
простых чисел
2, 3, 5, 7, …
Замечание. Заметим, что написать формулу общего члена последовательности или указать рекуррентный способ вычисления ее членов зачастую непросто. Например, несмотря на усилия многих математиков, до настоящего времени для последовательности простых чисел неизвестная ни формула общего члена последовательности, ни рекуррентный способ ее задания.
Числовую последовательность можно построить также и графически. Покажем это на следующем примере:
Пример. Построить график последовательности 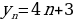 .
.
Это будет график функции 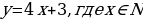 . Он состоит из точек прямой
. Он состоит из точек прямой 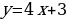 с абсциссами
с абсциссами 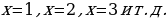
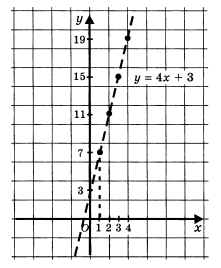
Итак, график любой числовой последовательности – это всегда график, состоящих из отдельных точек с натуральными абсциссами.
Ученики заканчивают заполнять схему:
С
 пособы задания числовой последовательности
пособы задания числовой последовательности
Аналитический Рекуррентный Описательный Графический
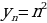
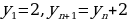 последовательность График,
последовательность График,
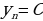
 простых чисел состоящий из
простых чисел состоящий из
2, 3, 5, 7, … отдельных точек
с натуральными
абсциссами
Вопросы оппонента:
-
Задать последовательность чисел, кратных 4: 4, 8, 12, 16, … аналитически, рекуррентно и графически.
-
Задает ли рекуррентное соотношение 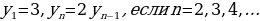 числовую последовательность, заданную аналитически:
числовую последовательность, заданную аналитически: 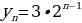
Ответы докладчика:
-
4, 8, 12, 16, …
Аналитический способ: 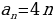
Рекуррентный способ: 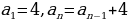
Графический способ:
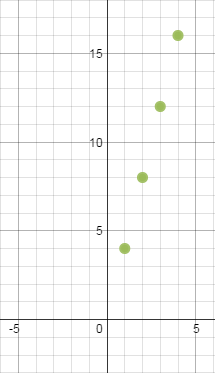
-
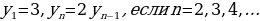
Выпишем несколько членов этой последовательности:
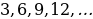
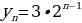
Выпишем несколько членов этой последовательности:
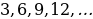
Вывод: эта одна и та же последовательность, заданная рекуррентно и аналитически.
Выступает 4 группа с докладом:
Числа Фибоначчи
Докладчик:
- Рассмотрим отдельно особый вид числовой последовательности – числа Фибоначчи. Для этого познакомимся с исторической справкой этих чисел.
В 1170 году в итальянском городе Пиза в семье нотариуса родился сын Леонардо. Его отец имел прозвище Боначчи – добряк, поэтому мальчика называли Фибоначчи – сын Боначчи. Под этим именем Леонардо Пизанский, ставший впоследствии известным математиком, часто упоминается в истории науки. Отец работал в Алжире в качестве представителя торгового дома своего города. Проживание в Алжире благоприятно сказалось на образовании Леонардо. В арабском мире наблюдался подъем математической науки. Ученые активно переводили античные труды с греческого языка на арабский и получили ряд новых серьезных результатов в области алгебры и тригонометрии.

Леонардо Пизанский (1170-1250)
Образование, полученное в Алжире, Леонардо постоянно пополнял во время путешествий с отцом, которому часто приходилось бывать по торговым делам в разных странах Средиземноморья. Внимательно изучив достижения арабской математики, Леонардо подытожил их в трактате «Книга абака» (1202). Написана она была для торговых и деловых людей с целью облегчения расчетов. В ней Леонардо познакомил широкий круг европейцев с десятичной системой счисления, которой пользовались арабы, и показал ее преимущество перед римской нумерацией, использовавшейся в Европе.
Помимо задач практического характера (о цене товара, о дележе наследства, об имуществе, о сплавах и растворах) книга содержала правило приближенного извлечения корней, способы решения систем линейных уравнений, неопределенных уравнений и их систем. Приводилась в этой книге и одна старинная задача, известная математикам еще с XIII в.:
Пара кроликов, начиная с двухмесячного возраста, ежемесячно производит новую пару. Сколько всего пар кроликов будет в конце года, если первая пара новорожденных кроликов появилась в январе (при условии, что все кролики останутся живы)?
В начале первого месяца была одна пара кроликов; в начале второго – две, причем одна из них зрелая, т.е. способная через месяц принести потомство, вторая – нет. Поэтому в начале третьего месяца будут три пары кроликов, две из них зрелые. В начале четвертого месяца станет пять пар (три пары были и две – новое потомство), из них только три зрелые и т. д.
Сказанное выше можно наглядно представить следующей схемой:
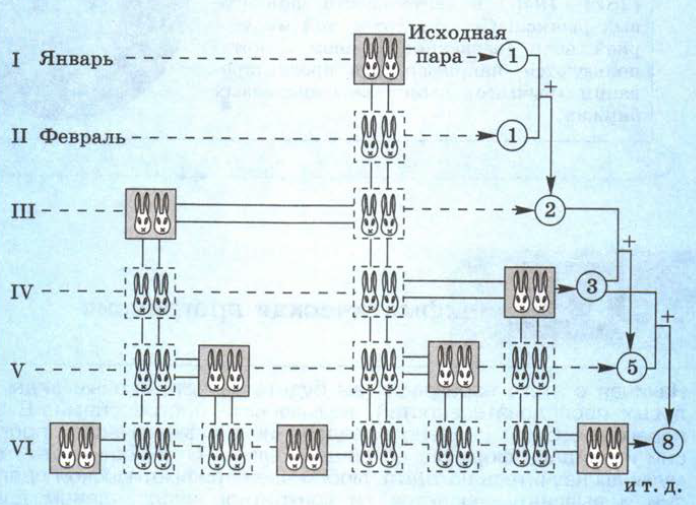
На схеме видно, как шел прирост кроликов в первые 6 месяцев. Если выписывать число пар по месяцам, то получим следующую последовательность чисел: 1; 1; 2; 3; 5; 8; … .
Эти числа с легкой руки французского математика Э. Люка стали называть числами Фибоначчи. Можно заметить закономерность, которой подчиняются эти числа: каждое число, начиная с третьего, равно сумме двух предыдущих. Другими словами, для чисел Фибоначчи выполняется рекуррентное соотношение:
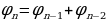 ,
, 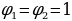 .
.
Однако можно указать формулу, позволяющую выразить 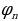 через n. Такая формула имеет вид:
через n. Такая формула имеет вид:
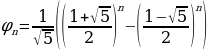 .
.
Это равенство называют формулой Бине по имени открывшего его (1843) французского математика Ж. Бине.
В математике существует одно замечательное отношение, которое называется золотым сечением. Архитектурные сооружения, построенные с соблюдением пропорций золотого сечения одни из красивейших творений человека.


Золотое сечение в архитектуре
Греки поняли, что золотое сечение появляется тогда, когда длина всего отрезка 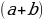 относится к длине его большей части
относится к длине его большей части 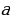 также, как
также, как 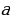 относится к
относится к 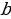 :
:

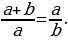
Было найдено, что золотое сечение равно 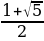 .
.
Числовой ряд Фибоначчи удобно использовать для нахождения приближенного значения золотого сечения. Отношение двух последовательных чисел из ряда Фибоначчи дает хорошее приближение к величине золотого сечения:
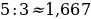 ;
;
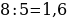 ;
;
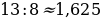 ;
;
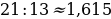 ;
;
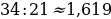 .
.
Таким образом, мы будем получать все более точные приближения числа 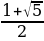 .
.
Удивительные факты проявления чисел Фибоначчи можно наблюдать в биологии, астрономии, экономике и т. д. Например, росток травы-чихун (тысячелистника птармика), когда появляется из земли, уже имеет один листок. Затем он вытягивается и дается еще один лист, затем через какое-то время вырастают сразу 2 новых листа, затем 3 листа, затем 5, потом 8, а после этого он выбрасывает 13 соцветий и т.д.

Числа Фибоначчи в тысячелетнике птармика
Красивейшие спирали в конфигурациях плодов и растений, в формах космических галактик имеют в основе своего построения те же числа Фибоначчи.




Числа Фибоначчи в природе
Закономерность, связанную с числами Фибоначчи, подметил американский финансист Ральф Нельсон Элиот (1871-1948) в деятельности финансовых рынков. Сегодня созданной им теорией волн (названной именем Элиота) пользуются, например, при прогнозировании «бычьего рынка» (рынка, на котором наблюдается тенденция роста цен) на финансовых биржах.

Ральф Нельсон Элиот (1871-1948)
Вопросы оппонента:
-
Сколько всего пар кроликов будет в конце года из задачи, приведенной в «Книге абака»?
-
Приведите все три способа задания чисел Фибоначчи.
Ответы докладчика:
-
Решение данной задачи удобно представить в виде схемы:
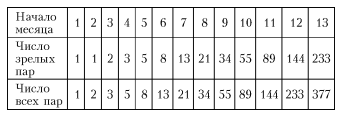
Тогда из таблицы видно, что в конце года в загоне окажется 377 пар кроликов.
-
Числа Фибоначчи:
Словесный способ: первые два члена последовательности равны 1; 3 член равен сумме 1 и 2 членов, т. е. 2; 4 член – сумме 2 и 3 членов, т. е. 3 и т. д.:
1, 1, 2, 3, 5, 8, 13, …
Рекуррентный способ: 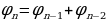 ,
, 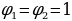 .
.
Аналитический способ: формула Бине:
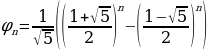
Учащиеся записывают все это в тетрадь.
Рефлексивно-оценочный этап
- Какова была цель урока? (Изучить понятие числовой последовательности, способы ее задания, а также познакомиться с некоторыми частными числовыми последовательностями, известными в математике )
- Достигли ли мы её? (Да, достигли)
- Как мы ее достигли? (Заслушали рефераты по истории возникновения и применения числовых последовательностей, понятиям, связанным с числовой последовательностью, способам задания числовой последовательности, числам Фибоначчи)
Домашнее задание:
Выучить теорию по §15 и записям в тетради, в задачнике § 15 № 15.1, 15.12 (а), 15.15
Рефераты
1. Основные понятия темы «Функция».
Вспомним для начала, что такое функция:
Определение. Функцией называется закон 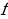 , по которому каждому элементу
, по которому каждому элементу  ставится в соответствие единственный элемент
ставится в соответствие единственный элемент 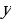 . При этом
. При этом 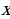 называют независимой переменной (аргументом), а
называют независимой переменной (аргументом), а 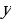 - зависимой переменной (функцией).
- зависимой переменной (функцией).
Можно привести многочисленные примеры функций. Вот некоторые из них:
-
зависимость между стороной квадрата а и его площадью 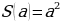
-
зависимость времени и температуры воздуха, наблюдавшейся в течение этого времени

Множество всех допустимых значений аргумента 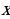 называется областью определения функции и обозначается
называется областью определения функции и обозначается 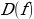 .
.
Множество всех значений, которые принимает зависимая переменная, называют множеством значений функции и обозначается 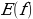 .
.
Примеры:
-

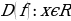
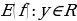
-
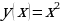
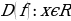
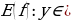
3)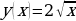
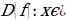
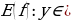
Функция, как известно, может быть задана несколькими способами:
-
Аналитический способ
Данный способ подразумевает задание формулы, позволяющей вычислить любое у, придавая различные значения x из X в этой формуле.
Пример. Зависимость стороны квадрата 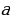 от его периметра P можно задать формулой:
от его периметра P можно задать формулой: 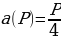
-
Табличный способ
Заключается в задании отдельных значений аргумента и соответствующих им значений функции. Данный способ не позволяет узнать, как ведёт себя функция за пределами таблицы, не хватает наглядности.
Пример:
Функцию 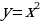 , заданную аналитически, можно представить в виде таблицы так:
, заданную аналитически, можно представить в виде таблицы так:
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| 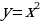
| 4 | 1 | 0 | 1 | 4 | 9 | 16 |
-
График
Для наглядного представления функциональной зависимости, используются специальные рисунки, называемые графиками. Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям независимой переменной, а ординаты - соответствующим значениям функции.
Пример. Зависимость долготы дня от времени года можно представить в следующем виде:

Напомним теперь, какая функция называется возрастающей, убывающей.
Определение. Функция 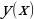 называется возрастающей на некотором промежутке, если для любых
называется возрастающей на некотором промежутке, если для любых 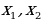 , принадлежащих данному промежутку, таких, что
, принадлежащих данному промежутку, таких, что 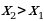 , выполняется неравенство
, выполняется неравенство 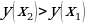 .
.
Примеры:
-
Функция 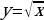 возрастает при
возрастает при 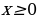
-
Функция 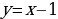 возрастает при
возрастает при 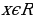
Определение. Функция 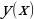 называется убывающей на некотором промежутке, если для любых
называется убывающей на некотором промежутке, если для любых 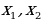 , принадлежащих данному промежутку, таких, что
, принадлежащих данному промежутку, таких, что 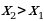 , выполняется неравенство
, выполняется неравенство 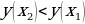 .
.
Примеры:
-
Функция 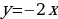 убывает при
убывает при 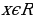
-
Функция 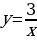 убывает при
убывает при 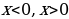
2. История возникновения и применения числовой последовательности. Основные понятия, связанные с числовой последовательностью.
В повседневной практике часто используется нумерация различных предметов, чтобы указать порядок их расположения. Например, дома на каждой улице нумеруются. В библиотеке нумеруются читательские абонементы и затем располагаются в порядке присвоенных номеров в специальных карточках. Иными словами, читательские абонементы располагают в определенной последовательности.
Можно привести и такой пример:
На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля будет на складе через 1 день, 2 дня, 3 дня и т. д.?
Если за х принять число дней, а за у – количество угля (в тоннах), то математической моделью ситуации будет линейная функция, заданная на множестве N натуральных чисел:
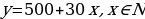 .
.
В результате мы получим следующую числовую последовательность:
530, 560, 590, …
Итак, уже здесь прослеживается функциональная зависимость количества угля от пройденных дней. Следовательно, перед нами функция, правда, определенная на специфическом множестве – множестве натуральных чисел. Поэтому вполне логично дать такое определение числовой последовательности:
Определение 1. Функцию 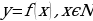 , называют функцией натурального аргумента или числовой последовательностью и обозначают
, называют функцией натурального аргумента или числовой последовательностью и обозначают 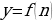 или
или 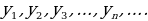
Итак, подчеркнем еще раз:
Область определения числовой последовательности: множество натуральных чисел.
Множество значений может быть какое-угодно.
Значения 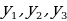 (и т.д.) называют соответственно первым, вторым, третьим (и т. д.) членами последовательности. В символе
(и т.д.) называют соответственно первым, вторым, третьим (и т. д.) членами последовательности. В символе  число n называют индексом, который характеризует порядковый номер того или иного члена последовательности (в записи
число n называют индексом, который характеризует порядковый номер того или иного члена последовательности (в записи 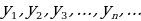 ).
).
Многоточия в обозначении последовательности (имеется в виду запись 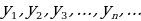 ) означают, что правее
) означают, что правее  располагаются дальнейшие члены последовательности (у4, у5, у6 и т.д.), рядом с уn находятся (а в случае необходимости и записываются)
располагаются дальнейшие члены последовательности (у4, у5, у6 и т.д.), рядом с уn находятся (а в случае необходимости и записываются) 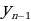 (слева) и
(слева) и 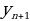 (справа). Члену
(справа). Члену 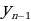 предшествует
предшествует 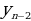 , а за
, а за 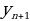 следует
следует 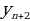 и т.д.
и т.д.
Для обозначения членов последовательности могут использоваться различные буквы, например: 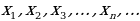 , или
, или 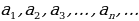 , или
, или 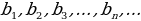 и т.д.
и т.д.
Последовательность, состоящая из конечного числа членов, называется конечной, а последовательность, состоящая из бесконечного числа членов, — бесконечной последовательностью.
Примеры конечных последовательностей:
-
Последовательность двухзначных чисел: 10, 11, 12, …, 99.
-
Последовательность однозначных четных чисел: 2, 4, 6, 8.
Примеры бесконечных последовательностей:
-
Последовательность степеней 2: 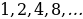 .
.
-
Последовательность четных чисел: 2, 4, 6, 8, … .
В математике существенный интерес представляют бесконечные числовые последовательности.
Сегодня числовые последовательности рассматриваются как частные случаи функции. Однако так было не всегда. Понятие числовой последовательности возникло и развивалось задолго до создания учения о функции. Вот примеры бесконечных числовых последовательностей, известных еще в древности:
-
1, 2, 3, 4, 5, … – последовательность натуральных чисел;
-
2, 4, 6, 8, 10, … – последовательность четных чисел;
-
1, 3, 5, 7, 9, … – последовательность нечетных чисел;
-
1, 4, 9, 16, 25, … – последовательность квадратов натуральных чисел;
-
2, 3, 5, 7, 11, …и – последовательность простых чисел;
-
1, 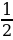 ,
, 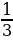 ,
, 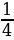 ,
, 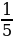 , … – последовательность чисел, обратных к натуральным.
, … – последовательность чисел, обратных к натуральным.
Число членов каждого из этих рядов бесконечно. Все перечисленные последовательности, кроме 5, являются заданными ввиду того, что для каждой из них известен общий член, т. е. правило получения члена с любым номером. Для последовательности простых чисел общий член неизвестен, однако еще в III в. до н. э. александрийский ученый Эратосфен указал способ (правда, очень громоздкий) получения n-го ее члена. Этот способ был назван «решетом Эратосфена».
Т. к. числовая последовательность – частный случай числовой функции, то у нее, как и у любой функции есть свойства. Ограничимся пока лишь свойством монотонности. Но вначале скажем, что такое монотонность. Введем два вспомогательных определения:
Определение 2. Последовательность 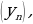 называется возрастающей, если каждый ее член (кроме первого) больше предыдущего:
называется возрастающей, если каждый ее член (кроме первого) больше предыдущего:
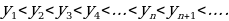
Пример 1:
Последовательность нечетных чисел: 1, 3, 5, 7, ..., 2n- 1, ... .
Действительно,
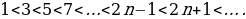
Определение 3. Последовательность 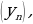 называют убывающей, если каждый ее член (кроме первого) больше предыдущего:
называют убывающей, если каждый ее член (кроме первого) больше предыдущего:
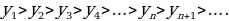
Пример 2:
Последовательность чисел, обратных к натуральным: 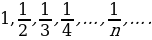
Действительно,
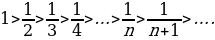
Тогда мы можем дать такое определение монотонной последовательности:
Определение 4. Возрастающие и убывающие последовательности образуют монотонную последовательность.
Примеры 1-2 иллюстрируют понятие монотонной последовательности.
Пример 3. 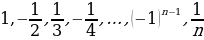 . Данная последовательность не является ни возрастающей, ни убывающей, т. к. в ней чередуются положительные и отрицательные числа. Поэтому данная последовательность не будет монотонной.
. Данная последовательность не является ни возрастающей, ни убывающей, т. к. в ней чередуются положительные и отрицательные числа. Поэтому данная последовательность не будет монотонной.
Оказывается, можно указать и признаки, позволяющие утверждать о возрастании или убывании некоторых последовательностей:
-
Если 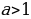 , то последовательность
, то последовательность 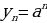 возрастает.
возрастает.
-
Если 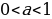 , то последовательность
, то последовательность 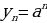 убывает.
убывает.
Примеры:
-
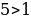 , тогда последовательность
, тогда последовательность 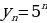 возрастает.
возрастает.
5, 10, 15, … .
-
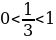 , тогда последовательность
, тогда последовательность 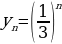 убывает.
убывает.
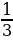 ,
, 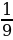 ,
, 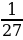 , … .
, … .
3. Способы задания числовой последовательности.
Как и функции, числовые последовательности можно задать четырьмя основными способами: аналитически, реккурентно, словесно и графически. Рассмотрим отдельно каждый из них.
Данный способ подразумевает задание формулы, позволяющей вычислить любой член последовательности по его номеру n. Сама формула при этом называется формулой общего члена последовательности.
Примеры:
-
Последовательность квадратов натуральных чисел задает формула: 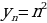 . Действительно, при
. Действительно, при
n = 1 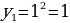
n = 2 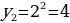
n = 3 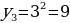
……..
-
Последовательность, состоящую из одного и того же числа: С, С, С, С, … , можно задать при помощи формулы 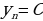 . Такая последовательность получила особое название – стационарная.
. Такая последовательность получила особое название – стационарная.
-
Последовательность нечетных чисел: 1, 3, 5, 7, 9, ... , задается при помощи формулы 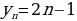 .
.
Действительно, при
n = 1 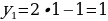
n = 2 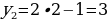
n = 3 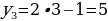
……..
Важный для приложений способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-ый член последовательности, если известны ее предыдущие члены. При вычислении членов последовательности по этому правилу мы как бы все время возвращаемся назад, выясняем, чему равны предыдущие члены. Такой способ задания последовательности называется рекуррентым (от лат. recurrere – возвращаться). Чаще всего в таких случаях указывают формулу, позволяющую выразить n-ый член последовательности через предыдущие, и задают один-два начальных члена последовательности.
-
Последовательность четных чисел: 2, 4, 6, 8, 10, ... , задается при помощи рекуррентного соотношения 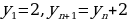 .
.
n = 1 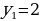
n = 2 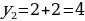
n = 3 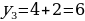
……..
-
Последовательность степеней 3: 1, 3, 9, 27, 81, 243, ... , задается при помощи рекуррентного соотношения  .
.
n = 1 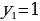
n = 2 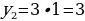
n = 3 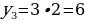
……..
В некоторых случаях для последовательности чисел не удается указать ни формулы общего члена последовательности, ни рекуррентного способа вычисления ее членов. В таких случаях последовательность задается описанием способа получения ее членов.
Примеры:
-
Последовательность 2, 3, 5, 7, 11, … простых чисел состоит из натуральных чисел, делящихся только на 1 и на себя.
-
Последовательность 3,1; 3,14; 3,142; 3,1416; 3,14159; … состоит из приближенных значений числа  с точностью до 0,1; 0,01; 0,001 и т. д.
с точностью до 0,1; 0,01; 0,001 и т. д.
Замечание. Заметим, что написать формулу общего члена последовательности или указать рекуррентный способ вычисления ее членов зачастую непросто. Например, несмотря на усилия многих математиков, до настоящего времени для последовательности простых чисел неизвестная ни формула общего члена последовательности, ни рекуррентный способ ее задания.
Числовую последовательность можно построить также и графически. Покажем это на следующем примере:
Пример. Построить график последовательности 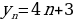 .
.
Это будет график функции 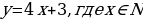 . Он состоит из точек прямой
. Он состоит из точек прямой 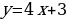 с абсциссами
с абсциссами 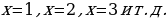

Итак, график любой числовой последовательности – это всегда график, состоящих из отдельных точек с натуральными абсциссами.
4. Числа Фибоначчи.
Рассмотрим отдельно особый вид числовой последовательности – числа Фибоначчи. Для этого познакомимся с исторической справкой этих чисел.
В 1170 году в итальянском городе Пиза в семье нотариуса родился сын Леонардо. Его отец имел прозвище Боначчи – добряк, поэтому мальчика называли Фибоначчи – сын Боначчи. Под этим именем Леонардо Пизанский, ставший впоследствии известным математиком, часто упоминается в истории науки. Отец работал в Алжире в качестве представителя торгового дома своего города. Проживание в Алжире благоприятно сказалось на образовании Леонардо. В арабском мире наблюдался подъем математической науки. Ученые активно переводили античные труды с греческого языка на арабский и получили ряд новых серьезных результатов в области алгебры и тригонометрии.

Леонардо Пизанский (1170-1250)
Образование, полученное в Алжире, Леонардо постоянно пополнял во время путешествий с отцом, которому часто приходилось бывать по торговым делам в разных странах Средиземноморья. Внимательно изучив достижения арабской математики, Леонардо подытожил их в трактате «Книга абака» (1202). Написана она была для торговых и деловых людей с целью облегчения расчетов. В ней Леонардо познакомил широкий круг европейцев с десятичной системой счисления, которой пользовались арабы, и показал ее преимущество перед римской нумерацией, использовавшейся в Европе.
Помимо задач практического характера (о цене товара, о дележе наследства, об имуществе, о сплавах и растворах) книга содержала правило приближенного извлечения корней, способы решения систем линейных уравнений, неопределенных уравнений и их систем. Приводилась в этой книге и одна старинная задача, известная математикам еще с XIII в.:
Пара кроликов, начиная с двухмесячного возраста, ежемесячно производит новую пару. Сколько всего пар кроликов будет в декабре, если первая пара новорожденных кроликов появилась в январе (при условии, что все кролики останутся живы)?
В начале первого месяца была одна пара кроликов; в начале второго – две, причем одна из них зрелая, т.е. способная через месяц принести потомство, вторая – нет. Поэтому в начале третьего месяца будут три пары кроликов, две из них зрелые. В начале четвертого месяца станет пять пар (три пары были и две – новое потомство), из них только три зрелые и т. д.
Сказанное выше можно наглядно представить следующей схемой:

На схеме видно, как шел прирост кроликов в первые 6 месяцев. Если выписывать число пар по месяцам, то получим следующую последовательность чисел: 1; 1; 2; 3; 5; 8; … .
Эти числа с легкой руки французского математика Э. Люка стали называть числами Фибоначчи. Можно заметить закономерность, которой подчиняются эти числа: каждое число, начиная с третьего, равно сумме двух предыдущих. Другими словами, для чисел Фибоначчи выполняется реккурентное соотношение:
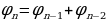 ,
, 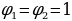 .
.
Однако можно указать формулу, позволяющую выразить 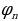 через n. Такая формула имеет вид:
через n. Такая формула имеет вид:
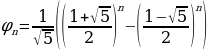 .
.
Это равенство называют формулой Бине по имени открывшего его (1843) французского математика Ж. Бине.
В математике существует одно замечательное отношение, которое называется золотым сечением. Архитектурные сооружения, построенные с соблюдением пропорций золотого сечения одни из красивейших творений человека.


Золотое сечение в архитектуре
Греки поняли, что золотое сечение появляется тогда, когда длина всего отрезка 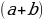 относится к длине его большей части
относится к длине его большей части 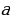 также, как
также, как 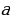 относится к
относится к 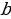 :
:

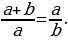
Было найдено, что золотое сечение равно 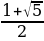 .
.
Числовой ряд Фибоначчи удобно использовать для нахождения приближенного значения золотого сечения. Отношение двух последовательных чисел из ряда Фибоначчи дает хорошее приближение к величине золотого сечения:
 ;
;
 ;
;
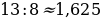 ;
;
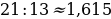 ;
;
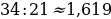 .
.
Таким образом, мы будем получать все более точные приближения числа 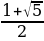 .
.
Удивительные факты проявления чисел Фибоначчи можно наблюдать в биологии, астрономии, экономике и т. д. Например, росток травы-чихун (тысячелистника птармика), когда появляется из земли, уже имеет один листок. Затем он вытягивается и дается еще один лист, затем через какое-то время вырастают сразу 2 новых листа, затем 3 листа, затем 5, потом 8, а после этого он выбрасывает 13 соцветий и т.д.

Числа Фибоначчи в тысячелетнике птармика
Красивейшие спирали в конфигурациях плодов и растений, в формах космических галактик имеют в основе своего построения те же числа Фибоначчи.




Числа Фибоначчи в природе
Закономерность, связанную с числами Фибоначчи, подметил американский финансист Ральф Нельсон Элиот (1871-1948) в деятельности финансовых рынков. Сегодня созданной им теорией волн (названнной именем Элиота) пользуются, например, при прогнозировании «бычьего рынка» (рынка, на котором наблюдается тенденция роста цен) на финансовых биржах.

Ральф Нельсон Элиот (1871-1948)
Решение домашнего задания:
№ 15.1
а) 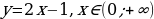
Нет, т. к. эта функция не является функцией натурального аргумента.
б) 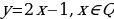
Нет, т. к. эта функция не является функцией натурального аргумента.
в) 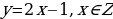
Нет, т. к. эта функция не является функцией натурального аргумента.
в) 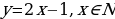
Да, т. к. эта функция является функцией натурального аргумента.
№ 15.12 (а)
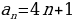
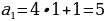
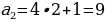
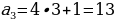
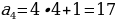
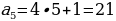
№ 15.15
-
1, 2, 3, 4, 5, …
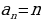
б) -2, -1, 0, 1, 2, …
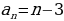
в) 6, 7, 8, 9, 10, …
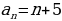
г) -1, -2, -3, -4, -5, …
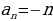







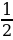 ,
, 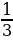 ,
, 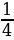 ,
, 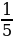 , … - последовательность чисел, обратных к натуральным.
, … - последовательность чисел, обратных к натуральным.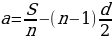 .
.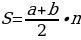
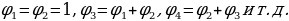 Другими словам, для чисел
Другими словам, для чисел 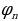 выполняется рекуррентное соотношение:
выполняется рекуррентное соотношение: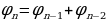 .
.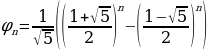 .
.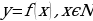 , называют функцией натурального аргумента или числовой последовательностью и обозначают
, называют функцией натурального аргумента или числовой последовательностью и обозначают 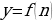 или
или 
 и т. д. называют соответственно первым, вторым, третьим (и т. д.) членами последовательности.
и т. д. называют соответственно первым, вторым, третьим (и т. д.) членами последовательности. число
число 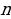 называют индексом, который задает порядковый номер того или иного члена последовательности.
называют индексом, который задает порядковый номер того или иного члена последовательности.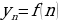 .
.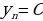 . Это значит, что речь идет о последовательности С, С, С, …, С, …, которую называют стационарной.
. Это значит, что речь идет о последовательности С, С, С, …, С, …, которую называют стационарной.
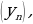 называется возрастающей, если каждый ее член (кроме первого) больше предыдущего:
называется возрастающей, если каждый ее член (кроме первого) больше предыдущего: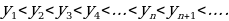
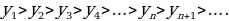
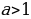 , то последовательность
, то последовательность 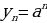 возрастает.
возрастает.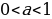 , то последовательность
, то последовательность 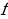 , по которому каждому элементу
, по которому каждому элементу  ставится в соответствие единственный элемент
ставится в соответствие единственный элемент 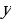 . При этом
. При этом 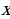 называют независимой переменной (аргументом), а
называют независимой переменной (аргументом), а 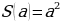

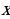 называется областью определения функции и обозначается
называется областью определения функции и обозначается  .
. .
.
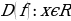
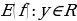
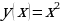
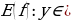
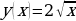
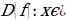
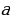 от его периметра P можно задать формулой:
от его периметра P можно задать формулой: 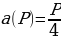
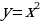 , заданную аналитически, можно представить в виде таблицы так:
, заданную аналитически, можно представить в виде таблицы так:
 пособы задания функции
пособы задания функции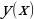 называется возрастающей на некотором промежутке, если для любых
называется возрастающей на некотором промежутке, если для любых 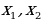 , принадлежащих данному промежутку, таких, что
, принадлежащих данному промежутку, таких, что 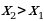 , выполняется неравенство
, выполняется неравенство 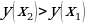 .
.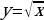 возрастает при
возрастает при 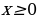
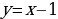 возрастает при
возрастает при 
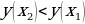 .
.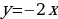 убывает при
убывает при 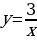 убывает при
убывает при 
 , если
, если 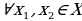
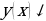 , если
, если 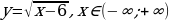
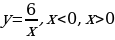
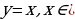
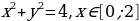
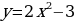
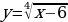
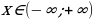 ставится в соответствие
ставится в соответствие 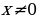 ставится в соответствие единственный элемент
ставится в соответствие единственный элемент 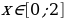 ставится в соответствие не единственный
ставится в соответствие не единственный 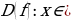
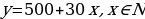 .
.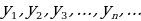 ).
). располагаются дальнейшие члены последовательности (у4, у5, у6 и т.д.), рядом с уn находятся (а в случае необходимости и записываются)
располагаются дальнейшие члены последовательности (у4, у5, у6 и т.д.), рядом с уn находятся (а в случае необходимости и записываются)  (слева) и
(слева) и  (справа). Члену
(справа). Члену 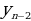 , а за
, а за 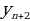 и т.д.
и т.д.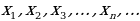 , или
, или 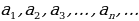 , или
, или 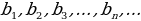 и т.д.
и т.д.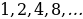 .
.
 исловые последовательности
исловые последовательности , если
, если 
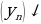 , если
, если 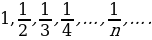
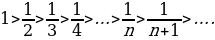
 чащиеся схематично это пишут в тетради так:
чащиеся схематично это пишут в тетради так: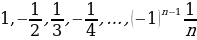 . Данная последовательность не является ни возрастающей, ни убывающей, т. к. в ней чередуются положительные и отрицательные числа. Поэтому данная последовательность не будет монотонной.
. Данная последовательность не является ни возрастающей, ни убывающей, т. к. в ней чередуются положительные и отрицательные числа. Поэтому данная последовательность не будет монотонной.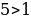 , тогда последовательность
, тогда последовательность 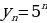 возрастает.
возрастает.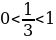 , тогда последовательность
, тогда последовательность 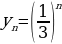 убывает.
убывает.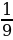 ,
, 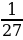 , … .
, … .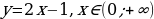
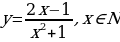
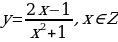
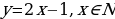

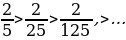
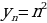 . Действительно, при
. Действительно, при 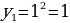
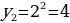
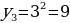
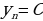 . Такая последовательность получила особое название – стационарная.
. Такая последовательность получила особое название – стационарная.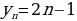 .
.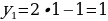
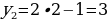
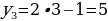
 пособы задания числовой последовательности
пособы задания числовой последовательности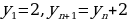 .
.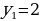
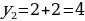
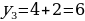
 .
.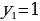
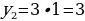
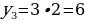
 пособы задания числовой последовательности
пособы задания числовой последовательности с точностью до 0,1; 0,01; 0,001 и т. д.
с точностью до 0,1; 0,01; 0,001 и т. д.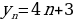 .
.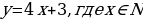 . Он состоит из точек прямой
. Он состоит из точек прямой 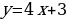 с абсциссами
с абсциссами 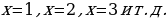

 пособы задания числовой последовательности
пособы задания числовой последовательности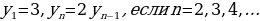 числовую последовательность, заданную аналитически:
числовую последовательность, заданную аналитически: 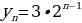
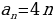
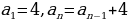

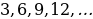


 .
.

 относится к длине его большей части
относится к длине его большей части 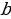 :
: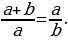
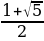 .
. ;
;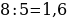 ;
;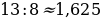 ;
;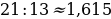 ;
;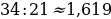 .
.






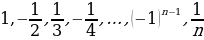 . Данная последовательность не является ни возрастающей, ни убывающей, т. к. в ней чередуются положительные и отрицательные числа. Поэтому данная последовательность не будет монотонной.
. Данная последовательность не является ни возрастающей, ни убывающей, т. к. в ней чередуются положительные и отрицательные числа. Поэтому данная последовательность не будет монотонной.