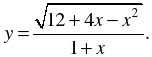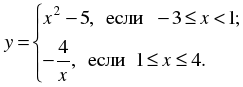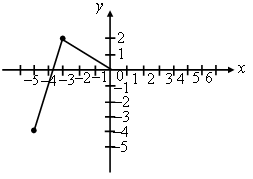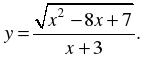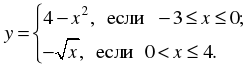Контрольная работа
Числовые функции
Цели: выявление знаний учащихся и степени усвоения ими изученного материала; развитие навыков самостоятельной работы.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение контрольной работы по вариантам.
В а р и а н т I
1. Найдите область определения функции 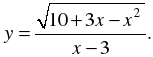
2. Постройте и прочитайте график функции
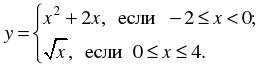
3. На рисунке изображена часть графика нечетной функции. Достройте график этой функции.

| 4. Какая из данных функций является четной, а какая – нечетной: а) у = 2 + 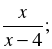 б) у = х(х2 – 9); в) у = б) у = х(х2 – 9); в) у = 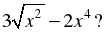 Приведите необходимые обоснования. |
5. Дана функция у = f(х), где f(х) = х – 4. Найдите все значения х, при которых справедливо неравенство f(х2) · f(х + 7) ≤ 0.
В а р и а н т II
1. Найдите область определения функции 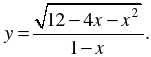
2. Постройте и прочитайте график функции
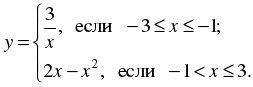
3. На рисунке изображена часть графика четной функции. Достройте график этой функции.
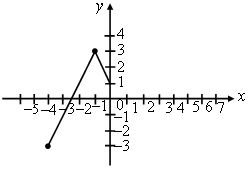
| 4. Какая из данных функций является четной, а какая – нечетной: а) у = 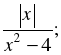 б) у = 2х – б) у = 2х – 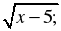 в) у = 3х – х5? в) у = 3х – х5? Приведите необходимые обоснования. |
5. Дана функция у = f(х), где f(х) = х – 1. Найдите все значения х, при которых справедливо неравенство f(х2) · f(х + 5) ≥ 0.
В а р и а н т III
1. Найдите область определения функции 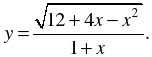
2. Постройте и прочитайте график функции
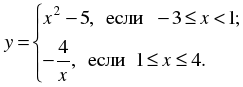
3. На рисунке изображена часть графика нечетной функции. Достройте график этой функции.
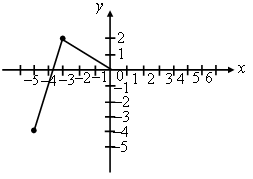
| 4. Какая из данных функций является четной, а какая – нечетной: а) у = х(х4 + 1); б) у = 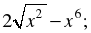 в) у = 1 – в) у = 1 –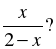 Приведите необходимые обоснования. |
5. Дана функция у = f(х), где f(х) = х – 4. Найдите все значения х, при которых справедливо неравенство f(х2) · f(х + 5) ≥ 0.
В а р и а н т IV
1. Найдите область определения функции 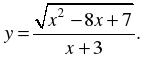
2. Постройте и прочитайте график функции
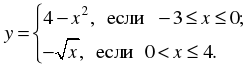
3. На рисунке изображена часть графика четной функции. Достройте график этой функции.

| 4. Какая из данных функций является четной, а какая – нечетной: а) у = | х (1 – х2); б) у = 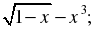 в) у = х5 + х? в) у = х5 + х? Приведите необходимые обоснования. |
5. Дана функция у = f(х), где f(х) = х – 4. Найдите все значения х, при которых справедливо неравенство f(х2) · f(х + 18) ≤ 0.







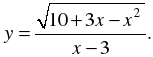
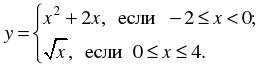

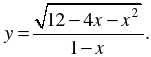
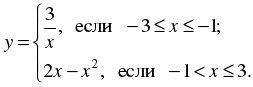
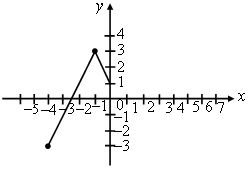
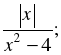 б) у = 2х –
б) у = 2х –