Доклад на тему: "Формирование ключевых компетенций на уроках геометрии"

Формирование ключевых компетенций учащихся на уроках геометрии

СОДЕРЖАНИЕ:

ВВЕДЕНИЕ……………………………………………………………………………………….3

1. О новых требованиях к школьному образованию……………………….5

1. ФГОС и современный урок...........................................................................7

1. Формирование ключевых компетенций учащихся на примере урока геометрии.………………………………………………………………...15

1. Заключение…………………………………………………………………17

1. Литература……………………………………………………………….....18

Введение

Геометрия - это целый мир, который окружает нас с самого рождения. Ведь все, что мы видим вокруг, так или иначе относится к геометрии, ничто не ускользает от ее внимательного взгляда. Геометрия помогает человеку идти по миру с широко открытыми глазами, учит внимательно смотреть вокруг и видеть красоту обычных вещей, смотреть , думать и делать выводы.

ФГОС выдвигает требования к формированию у школьников метапредметных результатов – универсальных учебных действий (личностных, познавательных, регулятивных и коммуникативных), которые должны стать базой для овладения ключевыми компетенциями, «составляющими основу умения учиться»

.Доктор педагогических наук А.В.Хуторской в своих работах по компетентностному подходу в обучении и воспитании отмечает, что «проблема современного образования заключается в том, что ученики могут хорошо овладеть набором теоретических знаний, но испытывают затруднения в использовании этих знаний для решения конкретных жизненных задач или проблемных ситуаций». Решению этой задачи и помогают уроки, на которых формируются ценностно–смысловые, учебно-познавательные, информационные, коммуникативные, социально-трудовые, общекультурные, природоведческие и здоровьесберегающие ключевые компетенции и компетенции личностного самосовершенствования. Ценность таких уроков ещё и в том, что способствует обобщению знаний самих учителей, которые обычно ограничены рамками своего предмета.

Результатом интеграции в 9 классе стала исследовательская работа «Правильные многоугольники в природе.Геометрия пчелиных сот».

Урок геометрии в 9 классе:

«Геометрия пчелиных сот»

Слайд №1.

Цели урока:

1.Проверить теоретические знания, практические навыки и умения использовать формулы зависимости между стороной правильного многоугольника и его площадью и периметром.

2.Показать связь между математикой и окружающей жизнью.

3.Активизировать мыслительную деятельность учащихся посредством каждого из них в работе.

4.Профессиональная ориентация.

Тип урока: Обобщающий урок по теме «Правильные многоугольники».

Оборудование: Учебник «Геометрия 7-9 класс» (Л.С.Атанасян) шаблоны правильных многоугольников: треугольников, квадратов, шестиугольников (все многоугольники с одинаковой длиной стороны), (пчелиные соты, воск, прополис).. доска, мультимедийное оборудование

Организационные формы общения: групповая, индивидуальная.

Структура урока

I этап: Организационный момент.

II этап: Мотивационно-ориентировочная часть.

III этап: Актуализация опорных знаний учащихся (устный опрос).

IV этап: Решение задач.

V этап: Минута релаксации.

VI этап: Работа с конструктором. Проверочная работа.

VII этап: Сообщение учителя и учащихся.

VIII этап: Домашнее задание, рекомендации по его выполнению.

IX этап: Подведение итогов.

X этап: Рефлексия

Ход урока.

I этап: Организационный момент.

II этап: Мотивационно-ориентировочная часть. Учитель: Изучая математику, мы постоянно проводим параллели, с повседневной жизнью, множество раз показывая, что человек на каждом шагу использует свои математические знания. И многие даже и не догадываются, что математикой пользуются и другие жители нашей планеты.Слайд №2

Пчёлы - удивительные творцы. Геометрические способности пчёл проявляются при построении сот. Они состоят из довольно тонких, близко расположенных друг к другу шестиугольников (т.е. составленные без просветов и перекрытий), стенки которых составляют примерно 0,1 мм.

Слайд №3

На этих шестиугольниках пчёлы оттягивают из воска ячейки, представляющие собой шестиугольные призмы. В них пчёлы выводят расплод, откладывают мёд, а потом снова покрывают (забрушёвывают) сплошным прямоугольником из воска.

Слайд №4.

Строгие геометрические пропорции ячеек давно обратили на себя внимание математиков. После тщательных расчётов они единодушно пришли к выводу, что пчёлы самым бережным образом научились делить большую площадь на несколько мелких частей. На практике решили труднейшую задачу по стереометрии: при минимальной затрате материала (воска) их ячейки построены так, что в них может помещено наибольшее количество мёда.

Слайд №5.

Учитель: Ребята, для того чтобы разглядеть в строительстве сотов применение геометрических правил, нужно обладать математическим взглядом.

III этап: Актуализация опорных знаний учащихся ( устный опрос).

1.Какой многоугольник называется правильным? Приведите примеры правильных многоугольников.

2. Как найти сумму углов правильного многоугольника.

3.Чему равны все углы правильного n-угольника?

IV этап: Приступаем к решению задач.

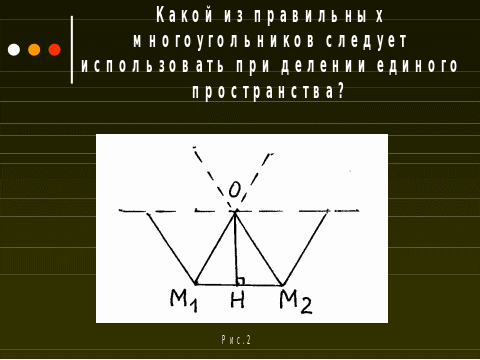
Задача 1.Пчелиные соты представляют собой прямоугольник, покрытый правильными шестиугольниками. Слайд №6

А, какой же ещё из правильных многоугольников следует использовать при делении единого пространства?

Слайд №7

Решение. Способ 1. Предположим, что плоскость покрыта n-угольниками, где каждая вершина является общей для x таких многоугольников,

ά – внутренний угол правильного многоугольника, равный ά=180⁰(n-2)/ n ( рис. 1), тогда 180⁰ (n-2)x/ n =360

Из этого равенства находим x=2n/(n-2)=2+4/(n-2). Учитывая, что x-целое, получаем n=3.4,6.

Делаем вывод: плоскость можно покрыть правильными треугольниками, квадратами и правильными шестиугольниками.

Способ 2.

Проверим при n=3. Три угла, плотно составленные дают 180⁰, шесть углов- 360⁰. Плоскость покрыта без просветов .

При n=4. Четыре угла плотно составленные дают 360⁰, т.е. 90 ∙ 4= 360⁰ .

Плоскость покрыта без просветов.

При n=5. Внутренний угол правильного пятиугольника равен 108⁰,

108⁰ ∙3=324⁰, остаётся просвет в 36^0.

При n=6. Внутренний угол правильного шестиугольника равен 120⁰, три шестиугольника составленные вместе, образуют 120⁰ ∙ 3=360⁰. Плоскость покрыта без просветов.

Слайд №8

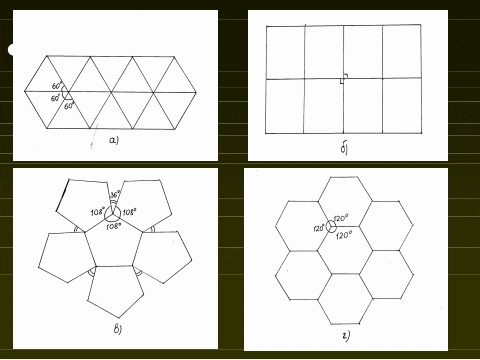
Вывод: плоскость без просветов можно покрыть лишь правильными треугольниками, квадратами и правильными шестиугольниками (если многоугольники одного вида).

Задача 2. Как пчёлы осознали устойчивость, преимущества шестиугольника перед равносторонним треугольником и квадратом? Для ответа на данный вопрос нужно проверить зависимость между стороной правильного многоугольника, его площадью и периметром, т.е. сравнить периметры этих разных многоугольников, имеющих одинаковую площадь.

Пусть даны, правильный треугольник, квадрат и правильный шестиугольник.

Слайд №9

У какого из этих многоугольников наименьший периметр?

Решение.

Слайд №10

Пусть S_n -площадь правильного n-угольника ,

М₁М₂=а_n, (рис.20)

S_n=n ∙ а_n²/4 tg (180⁰/ n).

Угол М₁ОН=180⁰/ n, где а_n- сторона n-угольника, угол М₁ О М₂= 360⁰/ n.

Имеем:

S₃= ∙а₃²/4, а₃² = 4∙ S₃/,

S₄=а₄², а₄² = S_{4 ,}

S₆= 6∙S₃= 6∙ (∙а₃²/4) =3∙а₆²/2, а₆² =(S₆∙2)/ 3∙.

Так как все площади равны т.е. S₃ = S₄ = S₆ обозначим их через S.

Р_n-периметр n-угольника. Возведём Р_n в степень для удобства сравнения.

Имеем:

Р₃ = 3∙а₃, Р²₃ = 9∙а₃²_, Р⁴₃ = (9∙а₃²)²=81∙а⁴₃=432 S².

Аналогично получим

Р⁴₄=256 S², Р⁴₆=192 S².

Например, S=16 см², при а₃=6 см² , а₄= 4 см², а₆= 2,5 см².

Очевидно, сравнив степени периметров, делаем вывод: что наименьший периметр при одинаковой площади у шестиугольника.

Учитель. Мы пришли к выводу, что пчелы изобрели самую совершенную геометрическую форму сот – шестигранник, что обеспечило наивысшую прочность этих хрупких восковых строений и исключительную экономию труда и воска.

V этап: Минута релаксации.

Слайды №11,12,13,14.

VI этап: Работа с конструктором.

О каких шедеврах, и каком устройстве сейчас идет речь?

Слайд №15

Чарует простота и сложность мирозданья.
Известен нам пространственный паркет.
Природы мудрые созданья
Шедевры строят много лет.

Именно пчёлы строят свои соты как раз в форме паркета.

Паркет- орнамент из фигур, заполняющих плоскость без промежутков. Делают они это без линейки и циркуля, без знания математики - им помогает инстинкт.

Вопрос 1? Где человек может использовать умение покрывать плоскость правильными многоугольниками?

Слайд №16

Слайд №17

Ответы учащихся:

- При изготовлении тротуарной плитки используют строение пчелиных сот.

- Мобильные, или сотовые, телефоны работают, благодаря созданию особой сотовой сети. Сеть создана по принципу устройства пчелиных сот. Система сотовой связи представляет собой совокупность ячеек, покрывающих обслуживаемую территорию.

-Особый сотовый заполнитель является одним из наиболее экономичных современных конструкционных материалов.

-Составление (создание) орнамента настоящее искусство. Им в совершенстве владеют архитекторы, дизайнеры, строители.

Практическая работа. Учащиеся выполняют работу, используя готовые шаблоны.Составить из правильных многоугольников двух цветов эскиз напольного паркета на картоне.

Вариант №1. Из правильных четырёхугольников и правильных треугольников.

Вариант №2.Из правильных шестиугольников, треугольников и квадрата.

Получившиеся образцы оцениваем.Слайд №18

Проверочная самостоятельная работа.

Вариант 1. На автобусной станции надо покрыть пол вестибюля прямоугольной формы, размеры которого 14.2 м и 8.5 м керамическими плитками двух цветов, причём плиток каждого цвета должно быть поровну. Сколько надо взять плиток каждого цвета, если плитка имеет форму правильного шестиугольника со стороной 12см. (1645 штук)

Вариант 2. Пол комнаты длиной 7,8м и шириной 5,5 м нужно покрыть плитками линолеума, имеющими форму правильного шестиугольника, сторона которого равна

16 см определите необходимое количество плиток, чтобы покрыть пол. (≈675 штук)VII этап: Сообщение учителя.

Слайд №19

Каждый, кто впервые знакомится с пчёлами, попадает в поразительно интересный, диковинный, можно сказать, фантастический мир, великолепно организованный и бесконечно гибкий, простой в своём естественном совершенстве и в тоже время беспредельно сложный.

Известно, например, что древние египтяне видели в пчелином гнезде государство во главе с пчелой- фараоном, который в окружении свиты слуг, обвевающих его опахалами усиков, наблюдают с высоты своего воскового трона, как караваны пчёл-рабов складывают к его стопам сладкие дары.

Одни пчёлы вползают в пустые ячейки, другие - медленно бродят по сотам, третьи – пятясь, выкарабкиваются из ячеек, четвёртые – юркие и подвижные - скользят мимо всех.По краю сотов, лениво ползёт толстый трутень. Матка торжественно ходит, волоча свое брюшко, и пчёлы расступаются, давая ей дорогу. Вот пчела, вернувшись, домой с приклеенным к задним ножкам цветными комочками цветочной пыльцы, поднимается на соты. Вот пчела- санитар, выбиваясь из сил, тащит из глубины гнезда труп осы. Вот другие пчёлы – уборщицы веерами крыльев подметают дно улья. С прилётной дощечки одна за другой ежеминутно поднимаются в воздух пчёлы. Навстречу летят другие. В каждом уголке гнезда кипит жизнь. Пчёлы строят соты, носят мёд, заполняют ячейки мёдом и закупоривают их. Они кормят весь улей, да и людей тоже, если человек умело с ними обращается.

Первый ученик.

Пчелиный мёд – ценнейший продукт. Мёду приписывают свойство сохранять юность и бодрость. Древнегреческий философ Демокрит (460-370 гг. до н.э.) проживший свыше ста лет, говорил, что для сохранения здоровья «внутренности следует орошать мёдом, а наружность маслом».

Химический состав мёда различен и зависит от вида растений. В мёде содержится около 100 различных веществ. Составной частью всех сортов мёда являются углеводы: глюкоза и фруктоза. Углеводы для организма человека являются энергетическим материалом. Из минеральных веществ в состав мёда входят соли кальция, натрия, магния, железа, серы, хлора, фосфора, а в некоторых сортах встречается и радий. Мёд содержит органические кислоты. И микроэлементы: марганец, кремний, алюминий, бор, хром, медь, литий, титан, йод, кобальт, молибден и другие. Мёд-это настоящая кладовая витаминов, где они прекрасно сохраняются. Обилие ценных веществ и витаминов делает мёд незаменимым продуктом питания, он широко используется человеком в народной медицине, в косметике.

Второй ученик.

Пчелиный яд представляет бесцветную прозрачную коллоидную жидкость с характерным запахом, напоминающим запах мёда, горьким жгучим вкусом. От одной пчелы можно получить 0.4-0,8 мг яда. Количество яда зависит от возраста пчелы, времени года и пищи. Пчелиный яд является очень сильным обеззараживающим веществом: даже в разведении 1:50 000 пчелиный яд стерилен. Жаля, пчела вводит примерно 0,0003 грамма яда. Серьёзно страдают от пчелиного яда иногда люди. Но тот же пчелиный яд успешно используется для исцеления таких болезней человека, как ревматизм, невралгия, бронхиальная астма и т. д.

Жало пчелы является орудием самозащиты, а не орудием нападения. Пчела не бросает своё засевшее в теле врага зазубренное жало, а отрывается от него, нанося себе этим смертельную рану.

Третий ученик.

Воск выделяется пчёлами непроизвольно, когда в гнездо поступает свежий корм. Воск вырабатывается особыми восковыми железами рабочей пчелы. Выделяют воск только молодые пчёлы в возрасте от 10-12 дней до 18-20. Воск богат витамином А. За сезон сильная пчелиная семья может дать от 0,8-1,2 кг воска. Воск легче воды, плавиться при температуре 60⁰. Воск входит в состав пластырей, мазей, кремов, Из воска готовят свечи и краски.

Четвёртый ученик.

Маточное молочко. Рабочие пчёлы вырабатывают железами особое высокопитательное вещество, которым они вскармливают личинку будущей матки. Это вещество и получило название маточного молочка. Личинка будущей матки буквально плавает в маточном молочке.

Учитель.

Пчеловодство-это занятие для души. По своему опыту знаю, если пчёл полюбить, эта любовь превращается в «болезнь», от которой ты уже не излечишься. Поэтому я хочу, чтобы вы полюбили пчёл и полюбили труд. Иногда ученик не может освоить школьную программу нормально а, талант в работе с пчёлами даёт ему возможность найти свою профессию и заработок на жизнь.

На протяжении веков все слои общества и все народы нашей земли не могли обойтись без практических математических знаний. Но, оказывается, что и насекомые пользуются математическими знаниями.

Скажите, что мы можем перенять из образа жизни пчёл?

Ответы учащихся:

- Медоносная пчела считалась символом верности, храбрости и презрения к смерти.

Ухаживая за пчёлами, учиться быть пунктуальными, воспитывать в себе сильный характер и укреплять нервы.

-Из образа жизни пчел можно для любого человека заимствовать понятие дружбы, толерантности, трудолюбия, настойчивость в достижении необходимого результата.

-Прикоснувшись к тайне математических шедевров из воска, ещё раз убеждаемся во всесторонней эффективности математики.

- Пчёлы изобрели самую совершенную геометрическую форму сот.
- На примере пчёл мы убедились, насколько гармонично устроен наш мир, как умна природа. Наша задача - беречь этот мир и разумно пользоваться его дарами.

VIII этап. Домашнее задание.

Выполнить проект напольного паркета составленного из:

1.Правильных восьмиугольников и четырёхугольников со стороной 4 см.

2.Правильных шестиугольников, треугольников и четырёхугольников со стороной 4 см.

IX этап. Рефлексия.

X этап. Итог урока.

Мы ответили на этот вопрос: шестиугольник самая оптимальная геометрическая форма для максимально полезного использования единицы площади и минимального расхода строительного материала. Пчелиные соты – это математический шедевр из воска.

Преподавание математики в соответствии с ФГОС общего образования

Хотелось бы, чтобы на уроке ученики поняли, что без знания геометрии нельзя познать окружающий мир, ведь не случайно на здании академии Платона было написано, что «не знающий геометрии, да не войдет в академию» и знания, полученные на этом уроке обязательно пригодятся в жизни, в независимости от того, какую профессию получат школьники. Мир – единое целое, в природе всё взаимосвязано и в том числе геометрия и биология также находятся в единой взаимосвязи.

ФГОС выдвигает требования к формированию у школьников метапредметных результатов – универсальных учебных действий (личностных, познавательных, регулятивных и коммуникативных), которые должны стать базой для овладения ключевыми компетенциями, «составляющими основу умения учиться».

Приоритетным направлением новых образовательных стандартов является реализация развивающего потенциала общего среднего образования.

Особое место в Стандарте отводится задаче формирования универсальных учебных действий, которые реализуют определённые функции: регуляция собственной учебной деятельности, создание условий для саморазвития и самореализации личности, готовность к непрерывному образованию на основе умения учиться.

Изучение правильных многоугольников в курсе геометрии основной школы является традиционным разделом и достаточно важным во всех периодах школьного образования. Многоугольники, несомненно, обладают красотой и используются в нашей жизни очень обширно. Многоугольники важны для нас, без них мы бы не смогли строить такие прекрасные здания, скульптуры, фрески, графики и многое другое. Математика владеет не только истиной, но и высшей красотой – отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которая свойственна лишь величайшим образцам искусства.

В курсе геометрии данная тема является актуальной, т.к. она используется при изучении других разделов геометрии – площадей, многоугольников, преобразованиях фигур, объёмов, многогранников.

Однако при изучении темы «Правильные многоугольники» возникают определённые трудности: при применении определений, изображений многоугольников к решению практических задач, при решении задач на построение, к доказательству теорем, запоминание формул для стороны правильного многоугольника через радиус описанной и вписанной окружности около правильного многоугольника, применение правильных многоугольников человеком в своей деятельности

Поэтому возникает необходимость в поиске наиболее эффективных форм и методов работы и с теоретическим материалом, и с задачным материалом по данной теме.

Основная цель, которая стоит передо мной, как учителем математики – научить детей самостоятельно добывать знания. А для этого необходимо: создавать образовательной среду обучающихся на основе системно-деятельностного подхода, создавать условия для развития познавательной активности обучающихся через использование в работе инновационных приемов и методов. На уроке формирование ключевых компетенций по геометрии по теме «Правильные многоугольники» проходила в форме что формирует ответственность за принятое решение. В соответствии с предложенными критериями учащиеся оценили работу через взаимопроверку. Обобщение знаний по геометрии – в форме обмена вопросами и самооценки ответов, что развивает критическое мышление учащихся.

Презентация по теме, творческие отчёты учащихся , работа с интерактивной доской – все это способствовало быстрому восприятию материала и формированию информационной культуры детей. Вся проделанная работа на уроке подвела школьников к мысли, что пчелы изобрели самую совершенную геометрическую форму сот – шестигранник с трехгранной пирамидой из опрокинутых ромбиков на ее дне, что обеспечило наивысшую прочность этих хрупких восковых строений и исключительную экономию места. Однако я как учитель математики предложила практически (при работе с бумагой) доказать эту мысль. Проведенное исследование по геометрии на вычисление периметров правильного треугольника, квадрата, правильного шестиугольника с равными площадями позволили школьникам сделать вывод, что наименьший периметр из всех фигур имеет правильный шестиугольник, а, значит, не случайно соты пчел имеют форму этой фигуры: мудрые пчелы экономят время и воск для построения сот. Исследовательская работа, решение задач, выдвижение гипотез и их проверка, работа с разверткой пчелиной ячейки помогает развивать пространственное воображение, творческое мышление учащихся, умение анализировать и работать в коллективе.

На данном уроке школьники увидели, что природные «пчелиные» законы используются человеком и при постройке ультрасовременных зданий, и при создании из образа жизни пчел можно для любого человека заимствовать понятие дружбы, толерантности, трудолюбия…сотовой сети. Была отмечена польза пчел для людей и то, что формирование ключевых компетенций через интеграцию курсов биологии и геометрии помогает созданию целостной картины мира в сознании учащихся и овладение ими знаний в комплексе.

Мы находимся в ситуации постоянного выбора, нас окружает быстро меняющийся мир. В будущем развитие общества будут определять люди умственного труда. Человек, получив профессиональную подготовку, порой вынужден менять профессию или постоянно повышать свою квалификацию. То есть выпускник современной школы должен уметь учиться. Задача учителя дать ученику опыт самостоятельной и исследовательской деятельности

Главной целью школьного образования является развитие ребёнка как компетентной личности путём включения его в различные виды ценностной человеческой деятельности: учёба, познание, коммуникация, личностное саморазвитие.

В теме «Правильные многоугольники» закладываются понятия основных видов правильных многоугольников и здесь же учащиеся знакомятся с основными видами задач, с методами их решения, оформления записи. В ходе изучения важно добиться, чтобы каждый ученик овладел всеми знаниями и умениями, необходимыми для дальнейшего успешного изучения новых понятий и теорем.

Особое внимание уделяется познавательной активности учащихся, их мотивированности к самостоятельной учебной работе. Это предполагает использование нетрадиционных форм уроков, использование компьютерных технологий на уроках, проектно- исследовательских работ.

1. Федеральный государственный образовательный стандарт общего основного образования /М-во образования и науки Рос. Федерации. – М.: Просвещение, 2011. 48 с.

2. Асмолов А.Г. Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий: пособие для учителя/под ред. А.Г. Асмолова. - М.: Просвещение, 2010. – 159 с.

3. . Азевич А.И. Геометрические вариации на пчелиную тему// Математика в школе.- М: Наука, 1998. №21 с. 32-38.

4. Атанасян Л.С. Геометрия. 7-9 классы: учебник для общеобразовательных учреждений. - М.: Просвещение, 2012. – 384с.

5. Боженкова Л.И. Планиметрия. Схемы, таблицы, УУД. Учебные материалы. – М., Калуга: КПГУ им. К.Э. Циолковского, 2012. – 62 с.

6. Гаврилова Н.Ф. Геометрия 8. Поурочные разработки по геометрии. Дифференцированный подход. М.: Вако, 2009 – 366 с.

7. Колмогоров А.Л. Паркеты из правильных многоуголь­ников // Библиотечка Квант. М.: Наука, 1976. № 3.