ЕГЭ 2024 вариант 10 задание 4

ЕГЭ 2024 вариант 10 задание 4

За круглый стол на 101 стул в случайном порядке рассаживаются 99 мальчиков и 2 девочки. Найдите вероятность того, что между девочками будет сидеть один мальчик.

Решение.

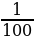Пусть первой за стол сядет девочка, тогда для каждого из оставшихся ребят (в том числе и для второй девочки ) вероятность оказаться на любом из оставшихся стульев равна . А мест, удовлетворяющих условию задачи, только два. Таким образом, вероятность, что между двумя девочками будет сидеть один мальчик равна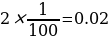

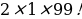Другое решение:

Число способов рассадить 101 человека на 101 стул равняется 101!.

Благоприятным для нас исходом будет вариант рассадки, когда на "первом" стуле сидит девочка, и через одно место справа сидит девочка, а на остальных девяноста девяти стульях произвольно рассажены мальчики. Количество таких исходов равно Так как "первым" стулом может быть любой из 101 стула (стулья стоят по кругу), то количество благоприятных исходов нужно умножить на 101. Таким образом, вероятность того, что между двумя девочками будет сидеть один мальчик равна

Ответ:0.02.