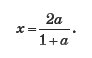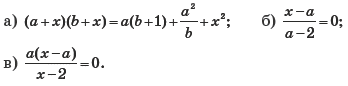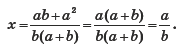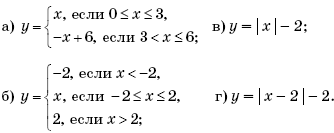Факультативный курс «Линейные уравнения и неравенства с параметрами»
Курс для учащихся 7-го класса, рассчитан на 32 учебных часа. Продолжительность занятия — два урока.
Программа курса
7. Тематическое планирование с определением основных видов учебной деятельности.
7 класс (32 часа)
| № | Содержание учебного материала | Кол-во часов | Обязательный минимум |
| 7 класс |
| 1. | Понятия постоянной и переменной величин | 2 | уметь находить закономерности в предложенных логических цепочках и рядах |
| 2. | Понятие линейного уравнения | 2 | уметь составлять логические цепочки и решать числовые головоломки |
| 3. | Общее решение линейных уравнений | 2 | уметь проводить рассуждения, используя последовательно все условия и приходить к выводу |
| 4. | Частные решения линейных уравнений | 2 | уметь составлять логические задачи и предлагать различные способы их решения |
| 5. | Решение линейных уравнений с параметрами | 2 | уметь владеть всеми изученными методами решения логических задач |
| 6-8 | Линейная функция и ее график | 2 |
|
| 9. | Уравнение с двумя переменными и его график. Координатная плоскость Oxa | 2 |
|
| 10. | Системы линейных уравнений с двумя неизвестными | 2 |
|
| 11. | Системы линейных уравнений | 2 |
|
| 12. | Решение линейных неравенств с одной переменной | 2 |
|
| 13. | Решение систем линейных неравенств с одной переменной | 2 | уметь проводить рассуждения, используя последовательно все условия и приходить к выводу |
| 14. | Линейные неравенства с двумя переменными и их системы | 2 | уметь владеть всеми изученными методами решения логических задач |
| 15. | Решение неравенств с параметрами. Плоскость Oxa | 2 | уметь находить закономерности в предложенных логических цепочках и рядах |
| 16. | Решение задач с параметрами |
| уметь составлять логические цепочки и решать числовые головоломки |
| Занятие № 1
Понятия постоянной и переменной величины |
Выбор обозначения той или иной величины — дело учащегося. При рассмотрении обозначений следует упомянуть, что встречаются случаи использования отдельных букв в качестве идентификаторов постоянных величин, например π.
Упражнение 1. Укажите постоянные и переменные величины, входящие в уравнения:
а) 7x – 1 = a; б) 6 = ax;
в) 5 – x = ax; г) ax + a = 1 + x;
д) a – x = a2x – 1; е) x = a – ax2;
ж) x = a3x; з) ax – a2 = 7;
и) ax – a2 = 4 – x.
Упражнение 2. Решите уравнения 1–4 (из упражнения 1):
а) при a = –1; 0; 1; б) при x = –1; 0; 1.
Данное упражнение позволяет понять, что все входящие в уравнение переменные равноправны и каждая из них может быть объявлена неизвестной (аргументом). Все оставшиеся переменные объявляются параметрами, которым присваиваются по умолчанию некоторые числовые значения, входящие в область определения данного аналитического выражения.
Упражнение 3. Решите относительно x уравнение:
а) 6x – 3y = 1; б) –x + 3a + y = 0;
в) –x + 2y = 5.
Упражнение 4. Решите относительно y уравнения из упражнения 3.
Эти упражнения позволяют показать, что приоритетная переменная может быть указана, тогда как другие переменные будут являться параметрами.
Упражнение 5. Выразите x через другие переменные, входящие в уравнение:
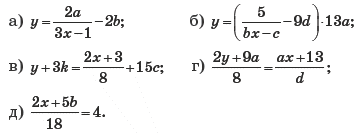
Задание на дом
1. При каких значениях параметра a уравнение имеет один корень? два корня? не имеет корней?
а) | x | = a; б) | x | = a2; в) | x | = a2 + 1.
2. Из равенства выразите сначала a через m,
а затем m через a:
а) 2a + 3m = 6; б) 9a – 2m = –18;
в) am + a = 4.
3. Сколькими способами можно заменить показатели m и n натуральными числами так, чтобы при любых значениях переменных x и y многочлен x6y2 + 6x4y2 + xmyn + 1 принимал положительные значения и степень многочлена была равна 8?
| Занятие № 2
Понятие линейного уравнения |
Следует обратить внимание на определение как степени одночлена, так и степени многочлена с несколькими переменными. Вместе с традиционными определениями вводится определение степени одночлена и многочлена относительно выделенной переменной.
Упражнение 1. Определите степень одночлена:
а) 5a3b9; б) –xy;
в) a4b11c; г) (–0,1)2c3y;
д) 3xmy; е) –xnyn.
Упражнение 2. Какова степень многочлена:
а) 3x8 – x3 – x8 + 6x – 2x8 – 1;
б) xy + 12x5y – 10x2y – 6?
Упражнение 3. Замените M каким-либо одночленом, чтобы получился многочлен четвертой степени:
а) M + 4x4 + 3x3 – x2 – 106;
б) 5x5 – M + 12x4 – x3 + x;
в) x + M + x4 – x5 – 3x2 – 1.
Упражнение 4. Какова степень многочлена в задании б) упражнения 2 относительно переменой x? относительно переменной y?
Далее дается определение линейного уравнения как уравнения вида f(x) = 0, где f(x) — двучлен первой степени относительно выделенной переменной (совершенно необязательно, чтобы обозначение этой переменной было x).
Упражнение 5. Укажите уравнения, линейные относительно переменной x, содержащие параметры:
а) x + 3 = 13x – 2; б) (a – 1)x = 3;
в) 12x – a = 12; г) bx – a = 1;
д) –5x = 4; е) 3x + 6 = 3(x – 1) + 4;
ж) 5 – x = (a + 1)x; з) 2x – (x – 19) = –x;
и) x = (a – 1)2x; к) 5x = 2 – (12 – 5x).
Упражнение 6. Найдите все значения параметра x, при которых уравнение (a2 + 1)x + a + 1 = 0
является линейным.
Решение. Выбрав переменную x в качестве параметра, мы тем самым сделали неизвестной переменную a. Уравнение (a2 + 1)x + a + 1 = 0 будет линейным относительно переменной a, если старшая степень этой переменной, входящей в уравнение, будет равна 1. Это возможно тогда, когда коэффициент при второй степени переменной a будет равен 0, то есть если значение параметра x будет равно 0.
Ответ: при x = 0.
Простейшими линейными уравнениями являются уравнения с одной переменной. Полезно вспомнить, что такие уравнения могут не иметь корней, иметь единственный корень, иметь бесконечное множество корней.
Упражнение 8. Решите уравнение:
а) x – 5 = 2; б) 2m + 3 = 4;
в) 2y – 3 = 3y – 2; г) 5(x + 1) – 2x = 3x + 5.
Упражнение 9.
а) Составьте линейное уравнение относительно переменной x, корнем которого является число 1.
б) Составьте линейное уравнение с целыми коэффициентами, корнем которого является число 0,4.
в) Составьте линейное уравнение с целыми коэффициентами, корнем которого будет являться любое действительное число.
г) Составьте линейное уравнение, не имеющее корней.
Задание на дом
1. Решите относительно x уравнение:
а) 5x – 10y = 2; б) –x + 3y = 7;
в) –x + 2a + m = 0; г) 2 – 11x + 3m = 2a.
2. Найдите все значения параметра a, при которых уравнение (a2 – 1)x2 + ax + 1 = 0 является линейным.
3. При каких значениях x выражение
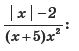
а) не имеет смысла;
б) равно нулю?
| Занятие № 3
Общее решение линейных уравнений |
Поскольку на занятии будет использовано понятие допустимых значений переменной, то уместно выполнить задание на повторение этого понятия.
Упражнение 1. При каких значениях переменной выражение имеет смысл:
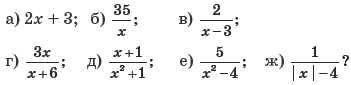
Объяснение нового материала полезно начать с задания, при выполнении которого учащиеся еще раз обратят внимание на управляющую роль параметра.
Упражнение 2. Решите уравнение
(m2 – m)x = 2m – 2
при m = 0; 1; 3.
Итак, мы подошли к введению алгоритма нахождения общего решения линейного уравнения.
Определение. Уравнение вида f(a)∙x = g(a), где f(a), g(a) — некоторые аналитические выражения, называется линейным относительно переменной x с параметром a. Если поставлена задача решить такое уравнение, это значит, что для каждого допустимого значения параметра a надо найти значение переменной x, удовлетворяющее этому уравнению.
Алгоритм решения:
1. Найти допустимые значения параметра.
2. Если f(a) = 0, то существование или отсутствие корней уравнения зависит от значения g(a). Если g(a) = 0, то уравнение принимает вид 0∙x = 0, и его корнем служит любое действительное значение переменной x. Если g(a) ≠ 0, то при любом значении переменной x возникает неверное числовое равенство, то есть уравнение корней не имеет.
3. Если f(a) ≠ 0, то получим, что 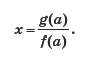
Можно раздать учащимся памятку в виде таблицы.

Упражнение 3. Решите уравнение относительно переменной x:
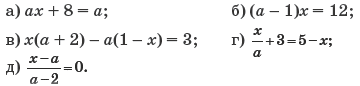
Решение. а) Приведем уравнение к виду ax = a – 8. Коэффициент при x равен a. Возможны два случая:
1) a = 0, тогда уравнение примет вид 0∙x = –8; следовательно, уравнение не имеет корней;
2) a ≠ 0, тогда ax = a – 8, 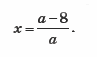
Ответ: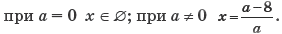
г) Приведем уравнение к виду 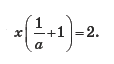
1) При a = 0 выражение 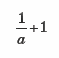 не имеет смысла. Значит, уравнение не имеет корней.
не имеет смысла. Значит, уравнение не имеет корней.
2) Если выражение равно 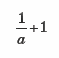 0 (то есть a = –1), то получим уравнение 0∙x = 2, которое не имеет корней.
0 (то есть a = –1), то получим уравнение 0∙x = 2, которое не имеет корней.
3) Если a ≠ 0 и a ≠ –1, то 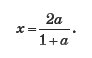
Ответ: при a = 0 или a = –1 x ∈ ѕ; при a ≠ 0 и a ≠ –1 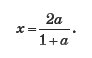
Данные упражнения помогают отработать алгоритм нахождения решения линейного уравнения с параметрами, при этом следует обратить внимание учащихся на влияние допустимых значений параметра. Упражнение 3 учитель должен разобрать, а упражнение 4 полезно предложить учащимся для самостоятельного решения.
Упражнение 4. Решите уравнение:
а) (k2 – 1)x = k + 1; б) ax – a = x – 1;
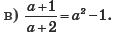
Задание на дом
1. Решите уравнение относительно x:
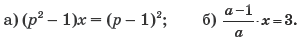
2. При каких значениях параметра a один из корней уравнения 5ax2 + 4x + a + 3 = 0 равен 0?
3. Какие из уравнений равносильны:
а) | x | + 1 = 0; б) x2 – 4 = 0;
в) x – 6 = 2x – (x + 2); г) x – 2 = 0:
д) | x | – 2 = 0?
| Занятие № 4
Частные случаи решения линейных уравнений |
Учащиеся должны усвоить, что решение уравнения с параметрами при заданных конкретных условиях — это частные решения уравнения. Например, задание может звучать так: «При каких значениях параметра... уравнение... имеет единственное решение (не имеет корней, имеет корень, равный... и т.д.).
Упражнение 1. Найдите значение параметра a, при котором уравнение ax – 3 = 2x – 1:
а) имеет корень, равный 4;
б) не имеет корней;
в) имеет бесконечно много корней.
Упражнение 2. При каких значениях параметра a равносильны уравнения:
а) 4(3x – a) – ax – 15 = 27 и 0,5(x – 4) + 8x = 15;
б) ax2 = 27 и x – 3 = 0?
Упражнение 3. При каких значениях параметра a уравнения ax = 12 и 3x = a имеют общие корни?
Упражнение 4. При каких целых значениях параметра a уравнение ax = 5 + 2x имеет целые корни? Найдите эти корни.
Решение. Приведем уравнение к виду (a – 2)x = 5. Если a ≠ 2, то 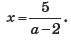 Чтобы x был целым числом, необходимо, чтобы значение выражения a – 2 было делителем числа 5, то есть a – 2 может быть равно 1; –1; 5; –5. Отсюда a = 3; 1; 7; –3.
Чтобы x был целым числом, необходимо, чтобы значение выражения a – 2 было делителем числа 5, то есть a – 2 может быть равно 1; –1; 5; –5. Отсюда a = 3; 1; 7; –3.
Ответ: при a = –3; 1; 3; 7.
Упражнение 5. При каких значениях параметра b уравнения 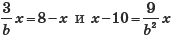 и не имеют корней?
и не имеют корней?
Упражнение 6. При каких значениях параметра n уравнение (n2 – 4)x = n3 – 2n2 – n + 2:
а) имеет единственный корень;
б) имеет бесконечное множество корней;
в) не имеет корней:
Решение. 1. Выражения n2 – 4 и n3 – 2n2 – n + 2 имеют смысл при любых значениях n.
2. Если n2 – 4 = 0, то n = ±2. При n = 2 значение выражения n3 – 2n2 – n + 2 равно 0. Получаем уравнение вида 0∙x = 0. Оно имеет бесконечное множество корней, то есть x — любое число. При n = –2 значение выражения n3 – 2n2 – n + 2 равно –12, получаем уравнение 0∙x = –12, не имеющее корней.
3. При n ≠ 2 и n ≠ –2 уравнение имеет единственный корень.
Ответ: а) при n ≠ 2 и n ≠ –2; б) n = 2; в) n = –2.
Упражнение 7. Составьте какое-либо уравнение вида ax + c = bx + d с переменной x, которое:
а) имеет корень, равный 7;
б) не имеет корней;
в) имеет бесконечное множество корней.
Задание на дом
1. При каких значениях параметра a уравнение a2(x – 5) = 25(x – a) не имеет корней?
2. При каких целых значениях параметра a корнем уравнения (a + 1)x = 4 будет целое число?
3. При каких значениях параметров a и b уравнение (a – b + 6)x – 3a + 1 = 0 имеет по крайней мере два корня?
| Занятие № 5
Решение линейных уравнений с параметрами |
Цель этого занятия — закрепить навык решения линейных уравнений с параметром и научиться использовать полученные навыки при решении нестандартных задач.
Упражнение 1. Решите уравнение относительно переменной x:
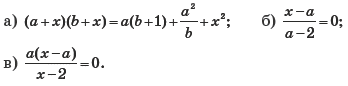
Решение. а) Приведем уравнение к стандартному виду, получим: 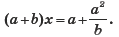
1. Допустимые значения переметных: a и x — любые числа, b — любое число, кроме 0. Значит, при b = 0 уравнение не имеет корней.
2. Если a + b = 0 (b ≠ 0), то есть a = –b, то уравнение принимает вид 0∙x = 0 и имеет бесконечное множество корней.
3. Если a ≠ –b, b ≠ 0, то уравнение имеет единственный корень 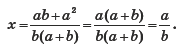
Ответ: при b = 0 x ∈ ѕ; при a = –b (b ≠ 0) x ∈ R;
при 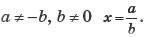
в) 1. Допустимые значения переменных: a — любое число, x — любое число, кроме 2.
2. Если a = 0, то уравнение примет вид
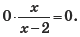
Отсюда x — любое число, кроме 2.
3. Если a ≠ 0, то x = a (x ≠ 2) — единственный корень уравнения. Так как x = a, но x ≠ 2, то получим, что при a = 2 уравнение не имеет корней.
Ответ: при a = 0 x ∈ R, x ≠ 2; при a = 2 x ∈ ѕ; при a ≠ 0, a ≠ 2 x = a.
Упражнение 2. При каких значениях параметра a уравнение (2a – 4)x + a – 1 = 4a – 7 имеет три различных корня?
Решение. Запишем уравнение в виде (2a – 4)x = 3a – 6. Линейное уравнение может иметь единственный корень, либо не иметь корней, либо иметь их бесконечное множество. Так как данное уравнение имеет три корня, значит, оно имеет вид 0∙x = 0. Отсюда должны выполняться условия 2a – 4 = 0 и 3a – 6 = 0. Тогда a = 2.
Ответ: a = 2.
Упражнение 3. Решите уравнение
(ax – 3a)(x – 2)(3 + x) = 0
относительно переменной x.
Упражнение 4. Решите уравнение
| x – 2 | + | x + a | = 0.
Решение. Так как каждое слагаемое неотрицательно, то сумма равна 0, если каждое слагаемое равно 0, то есть x – 2 = 0 и x + a = 0. Первое слагаемое равно нулю, если x = 2, но если x = 2, то второе слагаемое равно 0, если 2 + a = 0, то есть a = –2. Если a ≠ –2, то уравнение не имеет корней.
Ответ: при a = –2 x = 2; при a ≠ –2 x ∈ ѕ.
Упражнение 5. Решите уравнение
| x + 2 | + a2| x | = 0.
Упражнение 6. Найдите натуральные значения параметра a, при которых корень уравнения является числом натуральным:
а) a(3x – 2) + 2(3 + a) = 18;
б) 3x(a + 1) – 2a(x + 4) = 4(1 – 2a).
Задание на дом
1. При каком наибольшем натуральном значении параметра a уравнение 4(x – 2) = a – 15 имеет отрицательный корень?
2. Найдите значения параметра a, при которых уравнение 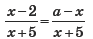 не имеет корней.
не имеет корней.
3. Даны функции y = x, y = 6 – 3x, y = a. При каких значениях параметра a в треугольнике, ограниченном графиками этих функций, будет содержаться ровно одна точка с целыми координатами?
| Занятие № 6
Линейная функция и ее график |
Линейной называется функция, задаваемая уравнением вида y = kx + b, где x — независимая переменная или аргумент, а k и b — произвольные действительные числа. Графиком линейной функции является прямая. Задавая конкретные значения параметров, мы выделяем из множества линейных функций одну или несколько функций, обладающих тем или иным свойством. Множество функций, обладающих указанным свойством, называют семейством функций, а множество их графиков — семейством графиков (семейством прямых).
Упражнение 1. Каким общим свойством будут обладать все графики функций, задаваемых уравнениями вида y = kx – 1?
Упражнение 2. Из множества линейных функций выделите семейство графиков, задаваемых уравнениями вида y = 2x + p.
Итак, задавая значение параметра b, мы выделяем семейство линейных функций, графики которых проходят через точку (0; b). Задавая значение параметра k, мы выделяем семейство линейных функций, графики которых параллельны прямой y = kx.
Упражнение 3. При каком значении k график функции y = kx + 2 проходит через точку A(1; 4), а при каких через точку B(–2; 0)?
Упражнение 4. График функции y = kx + b проходит через точки A(0; –4) и B(3; 5). Найдите значения k и b.
Упражнение 5. График функции y = kx + b проходит через точку B(3; 5) и параллелен графику функции y = 2x. Найдите значения k и b.
Полезно напомнить, что параметр k называют угловым коэффициентом. Если угловые коэффициенты равны, то прямые или параллельны (при b1 ≠ b2), или совпадают (при b1 = b2); если угловые коэффициенты различны — прямые пересекаются.
Упражнение 6. При каких значениях параметра a графики данных функций пересекаются:
а) y = (2a – 1)x и y = (4a + 3)x + 2a;
б) y = ax + 6a и y = ax?
Упражнение 7. При каких значениях параметра a графики данных функций параллельны:
а) y = (3 – a)x + 1 и y = (a – 1)x + 5;
б) y = (a – 3)x + 2a и y = (3 – 2a)x + a;
в) y = (a – 2)x + 6 – a и y = (2a – 3)x + 2a + 3?
Упражнение 8. При каких значениях параметра a графики данных функций совпадают:
а) y = 2ax + 7 и y = 4ax + 7;
б) y = (5a – 3)x + 2a – 1 и y = (a + 1)x + 14 + a;
в) y = (5a – 3)x + 3a и y = (5a + 1)x + 3a?
Упражнение 9. Проанализируйте, как изменяется наклон прямой в зависимости от параметра k, на примере функции y = kx (прямая пропорциональность).
Задание на дом
1. При каких значениях параметра a прямые y = –ax + 2 и 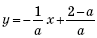 будут: пересекаться, совпадать, параллельны?
будут: пересекаться, совпадать, параллельны?
2. Найдите значения параметра a, при которых прямая y = ax + 2 пройдет через точку пересечения прямых y = 5x – 7 и y = 3x + 1?
3. Постройте графики функций:
а) y = | x |; б) y = | x | + 1; в) y = | x + 1 |.
| Занятие № 7
Линейная функция и ее график |
Цель этого занятия — познакомить учащихся с «плавающей» и «вращающейся» прямыми, разобрать решение задач с параметрами, где используются эти понятия. Учащиеся 7-го класса более подробно изучают только линейную функцию, а также знакомы с графиками вида y = x2 и y = x3. Однако им еще не знакомы преобразования графиков, а также не известны другие функции. Поэтому, чтобы расширить представление учащихся о графиках, полезно познакомить их с кусочно-заданными функциями и способами построения их графиков и еще раз обратить внимание на понятие области определения функции.
Упражнение 1. Постройте графики функций:
а) y = 1,5x – 2, где –2 ≤ x ≤ 2,
(график — отрезок);
б) y = 1,5x – 2, где x ≤ 2,
(график — луч, идущий влево,
с началом в точке (2; 1));
в) y = 1,5x – 2, где x ≥ –2,
(график — луч, идущий вправо,
с началом в точке (–2; –5)).
Упражнение 2. Постройте графики кусочно-заданных функций и графики функций, содержащих знак модуля:
а) в) y = | x | – 2;
б) г) y = | x – 2 | – 2.
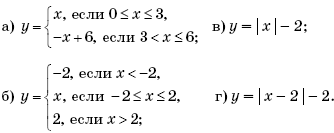
Далее знакомим учащихся с понятиями «плавающей» и «вращающейся» прямых.
Упражнение 3. Постройте семейство прямых:
а) y = a;
б) y = ax.
Семейство прямых, задаваемых уравнением вида y = a — это прямые, параллельные оси абсцисс («плавающая» прямая). Семейство прямых, задаваемых уравнениями вида y = ax — это прямые, проходящие через начало координат («вращающаяся» прямая). Полезным будет вспомнить, что с увеличением a прямая вращается против часовой стрелки.
Упражнение 4. Сколько общих точек имеют графики функций из упражнения 2 и прямая
y = a в зависимости от значения параметра a?
Решение.
Ответ:
а) при a a 3 — нет точек пересечения;
при 0 ≤ a при a = 3 — одна общая точка;
б) при a a 2 — нет точек пересечения;
при –2 a при a = ±2 — бесконечное множество общих точек;
в) при a при a = –2 — одна общая точка;
при a –2 — две общие точки;
г) при a при a = –2 — одна общая точка;
при a –2 — две общие точки.
Упражнение 5. Сколько общих точек имеют графики функций из упражнения 2 и прямая
y = ax в зависимости от значений параметра a?
Решение.
Ответ:
а) при a a 1 — одна общая точка;
при 0 ≤ a при a = 1 — бесконечное множество общих точек;
б) при a ≤ 0 или a 1 — одна общая точка;
при 0 a при a = 1 — бесконечное множество общих точек;
в) при a ≤ –1 или a ≥ 1 — одна общая точка;
при –1 a
Комментарий. В данном примере нужно обратить внимание учащихся на то, что количество общих точек будет зависеть от того, параллельна ли прямая y = ax какому-либо участку графика или нет. Условие параллельности — равенство угловых коэффициентов.
г) при a a ≥ 1 — одна общая точка;
при a = –1 — бесконечное множество общих точек;
при –1 a
Задание на дом
1. Сколько общих точек имеют прямая y = a и ломаная, задаваемая условием
2. Найдите все значения параметра a, при которых прямая y = ax пересечет в двух различных точках ломаную
3. Решите уравнение (a – 1)(a – 5)x = a – 1. Придумайте задачу с графиками функций, где пришлось бы решать данное уравнение.
| Занятие № 8
Линейная функция и ее график |
Упражнение 1. Найдите координаты точки пересечения прямых, заданных уравнениями
y = ax + 5 и y = 1,5x + 0,5b,
если известно, что график первой прямой проходит через точку A(–2; 3), а второй — через точку B(3; 4).
Упражнение 2. Найдите все значения параметра a, при которых графики функций
y = (2a – 3)x + a – 7 и y = (4a – 1)x + 5 – 3a
параллельны. Постройте графики этих функций при найденных значениях параметра a.
Статья опубликована при поддержке медицинского центра "ЦРЧ". "ЦРЧ" - это центр лазерной хирургии, подологии и проктологии. Центр предлагает Вам такие услуги, как лечение вросшего ногтя на пальце ноги, оперативная и консервативная ортопедия, мануальная терапия, удаление на коже лазером и другие. Узнать подробнее об услугах, цены и контакты Вы сможете на сайте, который располагается по адресу: http://www.rubca.net/.
Упражнение 3. Найдите общие точки функций
y = (4 – a)x + a и y = ax + 2.
Решение. Абсциссы общих точек двух графиков можно найти из уравнения
(4 – a)x + a = ax + 2.
Приведя уравнение к стандартному виду, получим:
(2a – 4)x = 2 – a.
Допустимые значения переменных — любые числа. Решим это уравнение относительно переменной x.
Если 2a – 4 = 0, то есть a = 2, то получим уравнение 0∙x = 0. Его корнями являются любые числа, поэтому графики функций совпадают. Общие точки графиков — прямая y = 2x + 2.
Если a ≠ 2, то x = –0,5, а ордината точки пересечения y = –0,5a + 2.
Ответ: при a = 2 координаты общих точек — (x; 2x + 2), где x — любое число;
при a ≠ 2 координаты общих точек — (–0,5; –0,5a + 2).
Упражнение 4. При каких значениях параметров b и k графики функций y = kx – 4 и y = 2x + b
симметричны относительно:
а) оси абсцисс; б) оси ординат?
Ответ: а) при b = 4, k = –2; б) при b = –4, k = –2.
Упражнение 5. Сколько общих точек имеет график функции
с графиком функции:
а) y = ax; б) y = ax + 3?
Упражнение 6. При каких значениях параметра b графики функций y = | x | + x – 2 и y = b:
а) не пересекаются;
б) пересекаются более чем в одной точке?
Упражнение 7. При каких значениях параметра c графики функций
и y = cx пересекаются в одной точке?
Задание на дом
1. При каких значениях параметра c графики функций y = | x | + 2 и y = cx пересекаются в одной точке?
2. Найдите все значения параметра a, при которых точка пересечения прямых x – y = a и 0,2y – x = 3
лежит на оси абсцисс.
3. При каких значениях параметра p прямая y = px + 2 образует с осями координат треугольник, площадь которого равна 16?
| Занятие № 9
Уравнение с двумя переменными и его график.
Координатная плоскость Oxa |
Равенство, содержащее две переменные, называется уравнением с двумя переменными. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство. Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых являются решениями этого уравнения. Соотнесение уравнения и геометрического места точек плоскости — один из самых важных шагов в развитии мышления учащихся.
Упражнение 1. Какие из пар чисел (–3; 9),
(–2; 4), (–1; 3), (0; 2), (1; –3), (2; 0), (3; 4) являются решениями уравнения:
а) x2 – y = 0; б) x + y = 2?
Упражнение 2. Постройте графики уравнений:
а) | x – 2 | = 0; б) 2x + 4y = 1;
в) | x – 1 | + (y + 2)2 = 0;
г) 2ax2 – 3x2 – 9y + 6ay = 0 при a = 1,5.
Ответ: а) прямая x = 2;
б) прямая y = –0,5x + 0,25;
в) точка (1; –2);
г) вся координатная плоскость.
Упражнение 3. Найдите все общие точки уравнений x2 – y = 0 и x + y = 2.
Ответ: (–2; 4), (1; 1).
Далее знакомим учащихся с графическим способом решения уравнений с параметром. При этом рассматриваем уравнение с параметрами как уравнение с двумя неизвестными, график которого существует, но только в плоскости Oxa. Сначала рассмотрим уравнение, которое может быть решено как графически, так и аналитически. Далее — уравнение, аналитический способ решения которого явно громоздкий.
Упражнение 4. Решите уравнение
(| x | – 4)(x + 2a) = 0.
Решение. Уравнение (| x | – 4)(x + 2a) = 0 можно решить как аналитически, так и графически. Разберем оба способа.
Способ I (аналитический). В данном случае произведение равно 0, если один из множителей равен 0, то есть | x | – 4 = 0 или x + 2a = 0. Отсюда x = ±4 или x = –2a.
Если –2a = ±4, то есть a = ±2, то уравнение имеет два корня: x = ±4,
Если a ≠ ±2, то три корня: x = ±4 или x = –2a.
Способ II (графический). Построим график уравнения в системе координат Oxa.
График уравнения — прямые x = 4, x = –4 и a = –0,5x. Проводим горизонтальные прямые
a = α. В зависимости от α находим решения уравнения как абсциссы точек пересечения прямой a = α с графиком уравнения (ось ординат не y, а параметр a).
Ответ: при a = ±2 x = ±4;
при a ≠ ±2 x = ±4 и x = –2α
Упражнение 5. Решите уравнение
(x2 – a2)(a – 1 – | x |) = 0.
Решение. Построим график уравнения
(x2 – a2)(a – 1 – | x |) = 0
в системе координат Oxa. Это прямые a = x, a = –x и график функции a = | x | + 1. Проводим горизонтальные прямые a = α. В зависимости от α находим решения уравнения как абсциссы точек пересечения прямой a = α с графиком уравнения. Получаем, что при a a; при a = 0 — один корень x = 0; при 0 a a; при a = 1 — три корня: x = 0 и x = ±a; при a 1 — четыре корня: x = ±a и x = ±a + 1.
Ответ: при a a a;
при a = 0 x = 0;
при a = 1 x = 0 и x = ±a;
при a 1 = ±a и x = ±a + 1.
Обратим внимание учащихся на то, что графическим способом удобно находить количество решений уравнения с параметрами.
Упражнение 6. При каких значениях параметра a уравнение имеет ровно три корня?
Решение.
Графиком уравнения будут парабола a = x2 и прямая x = –2. Необходимо также учесть область определения a ≠ x. Проводим горизонтальные прямые a = α и получаем, что уравнение будет иметь ровно три корня: при 0 a a a 4.
Ответ: при 0 a a a 4
уравнение имеет ровно три корня.
Задание на дом
1. Докажите, что уравнение
(a – | x – 1 |)(a + x2) = 0
при любых значениях параметра a имеет два различных корня.
2. Постройте графики уравнений:
а) | x – 1 | + (x + y)2 = 0; б) x2 = 4y2;
в) 
3. При каких значениях параметра a две прямые ax – y = –2a и x – ay = 2 будут пересекаться, совпадать или будут параллельны?
| Занятие № 10
Системы линейных уравнений с двумя неизвестными |
Одним из способов решения систем уравнений является графический способ.
Упражнение 1. Решите графически систему уравнений
Решение. Упростив формулу, задающую вторую функцию, получим: y = –x2, x ≠ ±2. Тогда график первого уравнения — прямая, а график второго уравнения — парабола с двумя выколотыми точками (x ≠ ±2).
Ответ: (–3; –9).
Упражнение 2. При каких значениях параметра a система

имеет единственное решение?
Решение. Решим задание графически. Построим в одной системе координат графики уравнений, входящих в систему, то есть y = | x | – 4 и y = ax. Из рисунка видно, что графики будут иметь одну общую точку при a ≤ –1 или a ≥ 1.
Ответ: при a ≤ –1 или a ≥ 1 система имеет единственное решение.
Упражнение 3. При каких значениях параметра a система
имеет решения?
Решение. Графиком первого уравнения системы является пара точек на координатной плоскости: (1; 2) и (–1; 2). График второго уравнения — прямая y = 0,5ax – 1,5. Чтобы система имела решения, необходимо, чтобы прямая проходила через точки (1; 2) или (–1; 2). Подставляя координаты этих точек в уравнение прямой
y = 0,5ax – 1,5, получим:
0,5a – 1,5 = 2 или –0,5a – 1,5 = 2.
Откуда a = 7 или a = –7.
Ответ: при a = ±7 система имеет решения.
Линейным уравнением с двумя переменными называется уравнение вида ax + by = c, где
a2 + b2 0, то есть значение хотя бы одного из коэффициентов (параметров) должно быть отлично от нуля. Графиком линейного уравнения с двумя переменными является прямая линия.
Определение. Системой двух линейных уравнений с двумя переменными называется система вида
где a1, a2, b1, b2 — действительные числа, причем
и

Определение. Решением системы двух линейных уравнений с двумя переменными называется упорядоченная пара значений этих переменных, обращающая в верное равенство каждое уравнение системы.
Так как каждому уравнению системы можно поставить в соответствие прямую, то решением системы будут являться координаты точек пересечения этих прямых.
Две прямые на плоскости могут быть параллельны, пересекаться или совпадать. В связи с этим и системы линейных уравнений могут иметь единственное решение, не иметь решений или иметь бесконечное множество решений. Для ответа на вопрос о количестве решений системы уравнений полезно заполнить с учащимися таблицу.
Алгоритм определения количества решений системы линейных уравнений
Упражнение 4. Найдите все значения параметра a, при каждом из которых система уравнений
не имеет решения.
Решение. Система не имеет решений, если выполняются условия

То есть должно быть

Отсюда a2 = 4, a = ±2.
Если a = 2, то a2 + a – 2 = 4, то есть  что неверно.
что неверно.
Если a = –2, то a2 + a – 2 = 0, то есть  что верно.
что верно.
Ответ: при a = –2 система не имеет решений.
Упражнение 5. Найдите все значения параметра a, при каждом из которых система уравнений
имеет бесконечно много решений.
Решение. Система имеет бесконечно много решений, если выполняются условия

то есть

Отсюда a2 – 3a = 0, то есть a = 0 или a = 3.
Если a = 3, то — верно.
Если a = 0, то — неверно.
Ответ: при a = –3 система имеет бесконечно много решений.
Упражнение 6. Найдите все значения параметра a, при каждом из которых система уравнений
имеет единственное решение.
Решение. Система имеет единственное решение, если выполняется условие  то есть
то есть 
Отсюда a2 ≠ 16, a ≠ ±4.
Ответ: при a ≠ ±4 система имеет единственное решение.
Упражнение 7. Для каждого значения параметра a определите число решений системы уравнений
Задание на дом
1. При каких значениях параметра a система
имеет:
а) одно решение;
б) бесконечно много решений;
в) не имеет решений?
2. Постройте графики уравнений:
а) | x – 1 | + (x + y)2 = 0; б) x2 = 4y2;
в) 
3. При каких значениях параметра a прямые ax – y = –2a и x – ay = 2 будут пересекаться, совпадать или будут параллельны?
| Занятие № 11
Системы линейных уравнений |
Упражнение 1. Числа a и b таковы, что система уравнений
имеет единственное решение (1; 1). Найдите a и b.
Решение. Если x = 1, y = 1 — решение системы, то при подстановке данных значений в систему получаем:
Отсюда a = 1, b = –1 или a = –1 и b = 1. Система должна иметь единственное решение. Проверим, выполняется ли условие  при найденных значениях параметров.
при найденных значениях параметров.
Если a = 1, b = –1, то  — верно.
— верно.
Если a = –1, b = 1, то  — неверно.
— неверно.
Ответ: при a = 1 и b = –1 система имеет единственное решение.
Упражнение 2. Найдите все значения параметра b, при каждом из которых система уравнений
имеет бесконечное множество решений, причем одно из этих решений x = 1, y = 3.
Упражнение 3. При каких значениях параметров a и b равносильны системы уравнений
Решение. Системы уравнений равносильны, если имеют одинаковые множества решений. Графиком каждого уравнения этих систем является прямая, причем прямые второй системы пересекаются  Значит, и прямые первой системы также должны пересекаться, причем в той же точке. Итак, все четыре прямые пересекаются в одной точке. Найдем эту точку, решив систему Решение системы — точка (3; 0). Подставив ее координаты 4
Значит, и прямые первой системы также должны пересекаться, причем в той же точке. Итак, все четыре прямые пересекаются в одной точке. Найдем эту точку, решив систему Решение системы — точка (3; 0). Подставив ее координаты 4
в уравнения с параметрами, получим: 3a = b + 1 и 6 = a2 + 2. Откуда a = 2, b = 5
или a = –2, b = –7. Проверим, пересекаются ли уравнения первой системы при найденных значениях параметров, то есть выполняется ли условие 
Если a = 2, b = 5, то условие  не выполняется
не выполняется  значит, найденные значения параметров не подходят.
значит, найденные значения параметров не подходят.
Если a = –2, b = –7, то получим:  что верно.
что верно.
Ответ: при a = –2, b = –7 системы уравнений равносильны.
Упражнение 4. Решите систему уравнений
Упражнение 5. Решите систему уравнений
Решение. Выразим из второго уравнения переменную x и подставим в первое уравнение системы. Получим:
Преобразуем первое уравнение системы к виду: a(a + 3)y = –(a + 3). Допустимые значения переменных — любые числа. Коэффициент при y равен 0, если a = 0 или a = –3. При a = 0 получим уравнение 0жy = –3, которое не имеет корней. При a = –3 получим уравнение 0∙y = 0, которое имеет бесконечное множество корней, y— любое число. Если a ≠ 0 и a ≠ –3, то уравнение имеет единственный корень 
Ответ: при a = 0 система не имеет решений;
при a = –3 x = 1 + 3y, y ∈ R;
при a ≠ 0 и a ≠ –3 x = 2, 
Упражнение 6. При каких значениях параметра a система
имеет единственное решение? Найдите это решение.
Решение. Решим задачу графически. Построим графики уравнений системы в одной системе координат и по рисунку определим, при каких значениях параметра a графики имеют одну общую точку. y = | x + 2 | — прямой угол с вершиной в точке (–2; 0). y = ax + 1 — «вращающаяся» прямая, центр вращения — (0; 1). Чтобы определить угловой коэффициент прямой y = ax + 1, проходящей через вершину «угла», подставим ее координаты в уравнение прямой. Получим: –2a + 1 = 0, отсюда
a = 0,5. Если a ≤ –1, то абсциссу точки пересечения находим из уравнения x + 2 = ax + 1.
Отсюда
Аналогично при a 1.
Ответ: при a ≤ –1 решение системы точка  при a = 0,5 — точка (–2; 0); при
при a = 0,5 — точка (–2; 0); при
a 1 — точка 
Задание на дом
1. При каких значениях параметра p система уравнений
имеет решение?
2. При каких значениях параметра m система линейных уравнений
3
имеет одно решение, бесконечно много решений, не имеет решений?
3. Зная, что a а) 3a и 3b; б) –5a и –5b;
в) a – 4 и b – 4; г) 
4. Верно ли, что если a а) a + 3 a – 6 в) 2a a
| Занятие № 12
Решение линейных неравенств с одной переменной |
Рассмотрение данной темы следует начинать с краткого повторения решения линейных неравенств с одной переменной.
Упражнение 1. Решите линейное неравенство:
а) 2x 22; б) –5x ≥ 30;
в) –0,1x ≤ 4; г) 0∙x д) 0∙x 0; е) 0∙x ≤ 0;
ж) 0∙x ≥ –3; з) 2x – 4 5 – x;
и)  к)
к) 
л)  м) 3 – 2x Упражнение 2. Найдите все значения параметра a, при каждом из которых корень уравнения
м) 3 – 2x Упражнение 2. Найдите все значения параметра a, при каждом из которых корень уравнения  — отрицательное число.
— отрицательное число.
Упражнение 3. При каких значениях параметра a каждое решение неравенства
(3x + 1)2 – 3 ≥ 9x(x + 2) – a
является решением неравенства
3x + a ≤ 2x + 1?
Решение. Решим первое неравенство:
9x2 + 6x + 1 – 3 ≥ 9x2 + 18x – a, 12x ≤ a – 2, 
Решим второе неравенство: x ≤ 1 – a. Чтобы каждое решение первого неравенства являлось решением второго, необходимо, чтобы 
Отсюда: a – 2 ≤ 12 – 12a, 
Ответ: при 
Упражнение 4. При каких значениях параметра a хотя бы одно решение неравенства 
будет являться решением неравенства 3 – 0,5x a?
Решение. Решив первое неравенство относительно x, получим: 8x – 8a – 12a – 12x ≤ 96,
x ≥ –5a – 24. Решив второе неравенство относительно x, получим: x a. Для того, чтобы хотя бы одно решение первого неравенства являлось решением второго, необходимо, чтобы 6 – 2a –5a – 24. Откуда a –10.
Ответ: при a –10.
Далее разберем алгоритм решения линейных неравенств с параметрами:
1) решение линейных неравенств с одной переменной и положительным коэффициентом при этой переменной;
2) решение линейных неравенств с одной переменной и отрицательным коэффициентом при этой переменной;
3) решение неравенств с коэффициентом, равным нулю. Данный момент требует особенно пристального рассмотрения. Результат разбора полезно записать в виде таблицы.
Алгоритм решения линейных неравенств с одной переменной
Упражнение 5. Решите неравенство
(a – 1)x ≤ a2 – 1
относительно переменной x.
Решение. Рассмотрим три случая.
1. a – 1 = 0. Тогда неравенство примет вид 0∙x ≤ 0, и его решением является любое значение переменной x.
2. a – 1 0. Тогда (a – 1)x ≤ a2 – 1 ⇔ x ≤ a + 1.
3. a – 1 Тогда (a – 1)x ≤ a2 – 1 ⇔ x ≥ a + 1.
Ответ: при a = 1 x ∈ R;
при a 1 x ≤ a + 1;
при a a + 1.
Упражнение 6. Решите неравенство
(a – 1)2x ≤ a2 – 1
относительно переменной x.
Задание на дом
1. Решите неравенство (a – 2)x a2 – 4 относительно переменной x.
2. При каких значениях параметра a каждое решение неравенства 0,3x – 6 а) принадлежит промежутку (–∞; 2);
б) решением неравенства является промежуток (–∞; 2)?
3. При каких значениях параметра a множество решений неравенства 0,3x – 6 a содержит ровно 5 натуральных чисел?
| Занятие № 13
Решение систем линейных неравенств с одной переменной |
Упражнение 1. Решите систему неравенств:
Упражнение 2. Найдите целые решения системы неравенств
Упражнение 3. При каких значениях параметра a множество решений системы  содержит ровно 5 целых решений?
содержит ровно 5 целых решений?
Решение. Решив первое неравенство, получим: x –2,8. Целые решения данного неравенства: –2; –1; 0; 1; 2... Решив второе неравенство, получим x a. Чтобы система имела ровно пять целых решений, необходимо, чтобы 0,5a 2, то есть a 4. С другой стороны, a не может быть больше 6 (полезно оговорить случай, когда 0,5a = 3), так как тогда система будет иметь более пяти целых решений. Значит, 0,5a ≤ 3, то есть a ≤ 6.
Ответ: при 4 a ≤ 6 система имеет пять целых решений.
Упражнение 4. При каких значениях параметра a система не будет иметь решений?
Решение. Решая первое неравенство, получим:  Решая второе неравенство, получим:
Решая второе неравенство, получим:
x 1 – a. Чтобы система не имела решений, необходимо, чтобы  (случай
(случай  обсудить отдельно). Из последнего неравенства следует: a ≤ –0,2.
обсудить отдельно). Из последнего неравенства следует: a ≤ –0,2.
Ответ: при a ≤ –0,2 система не имеет решений.
Упражнение 5. При каких значениях параметра a решением системы уравнений  является пара положительных значений x и y?
является пара положительных значений x и y?
Решение. Решая систему способом сложения, получим:
откуда
так как x 0 и y 0, то получим систему неравенств
Отсюда a 3.
Ответ: при a 3 решением системы является пара положительных чисел.
Упражнение 6. При каких значениях параметра b корень уравнения 6 – 3b + 4bx = 4b + 12x меньше 1?
Решение. 6 – 3b + 4bx = 4b + 12x,
(4b – 12)x = 7b – 6.
Если b = 3, то уравнение примет вид 0∙x = 15 и не будет иметь корней.
Если b ≠ 3, то 
По условию  Тогда
Тогда 
Дробь отрицательна, если числитель и знаменатель имеют разные знаки.
Поэтому
Решив обе системы, получим: –2
Ответ: при b ∈ (–2; 3) корень уравнения меньше 1.
Упражнение 7. Решите систему неравенств 
Решение. Решая первое неравенство системы, получим: (a – 1)x ≤ 1.
Если a – 1 — число отрицательное, и система имеет решения x 2.
Если a – 1 = 0, то решения первого неравенства — x ∈ R, а решения системы — x 2.
Если a – 1 0, то  Здесь возможны три случая:
Здесь возможны три случая:  или
или  Рассмотрим эти случаи.
Рассмотрим эти случаи.
1. Пусть  тогда
тогда  откуда
откуда
Имеем: 1 a
2. Пусть  тогда a = 1,5, но система при этом не имеет решений.
тогда a = 1,5, но система при этом не имеет решений.
3. Пусть  тогда
тогда  откуда
откуда
Вторая система не удовлетворяет условию, что a – 1 0. Решением первой системы является неравенство a 1,5. В этом случае система также не имеет решений.
Ответ: при a ≤ 1 x 2;
при 1 a ≤ 1,5 
при a ≥ 1,5 — нет решений.
Задание на дом
1. При каких значениях параметра a система неравенств будет иметь решение?
2. При каких значениях параметра m система неравенств  имеет ровно три целых решения?
имеет ровно три целых решения?
3. На координатной плоскости изобразите множество точек, координаты которых удовлетворяют условиям:
а) | x | в) | x |
| Занятие № 14
Линейные неравенства с двумя переменными и их системы |
Неравенство вида F(x; y) ∨ 0 называется неравенством с двумя переменными x и y. Решением данного неравенства является множество упорядоченных пар чисел (x; y), обращающих неравенство в верное числовое неравенство.
Упражнение 1. Являются ли пары чисел (1; 0), (–3; 1), (0; 3), (8; 4) решениями неравенства
4x – 2y + 6 ≥ 0?
Решить неравенство F(x; y) ∨ 0 в большинстве случаев можно лишь графически, указав геометрическое место точек (ГМТ), удовлетворяющих неравенству. Если уравнение F(x; y) = 0 определяет лишь некоторую линию, то множество точек плоскости, не лежащих на этой кривой, состоит из некоторого числа областей G1, G2, ..., Gn, на которые данная кривая разбивает плоскость. В каждой точке этих областей выражение F(x; y) определено и либо положительно, либо отрицательно.
Упражнение 2. F — множество точек плоскости, координаты которых удовлетворяют неравенству x2 + y2
| а) A(–1; 0);
в) C(2; 3); | б) B(5; –1);
г) E(3; 0)? |
Упражнение 3. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют неравенству:
а) y ≥ 2| x | – 2; б) (x – 1)(y + 2) ≥ 0;
в) x2 – 4y2 ≤ 0.
Решение. а) График уравнения y = 2| x | – 2 разбивает плоскость на две области. Возьмем «контрольную» точку, чтобы определить, в какой из областей выполняется неравенство. Например, при подстановке координат точки A(0; 0) в неравенство получаем: 0 2| 0 | – 2, что верно. Значит, точка A лежит в нужной нам области.
б) Графиком уравнения являются пересекающиеся прямые x = 1 и y = –2. Используя контрольные точки, проверим, какие из областей изображают решение неравенства.
A(0; 0): (0 – 1)(0 + 2) ≥ 0 — неверно;
B(2; 2): (2 – 1)(2 + 2) ≥ 0 — верно;
C(3; – 3): (3 –1)(–3 + 2) ≥ 0 — неверно;
E(–3; –3): (–3 – 1)(–3 + 2) ≥ 0 — верно.
Простейшей линией на плоскости является прямая, разбивающая плоскость на две полуплоскости. Ордината любой точки верхней полуплоскости больше ординаты соответствующей ей точки прямой y = kx + b. В этой полуплоскости выполняется неравенство y kx + b. В полуплоскости, расположенной ниже прямой y = kx + b, выполняется неравенство y
Упражнение 4. Изобразите множество точек координатной плоскости, координаты которых удовлетворяют неравенству:
а) y ≥ 2x – 2; б) y ≤ x + 2;
в) 2y + 2x – 3 ≤ 0.
Упражнение 5. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют системе неравенств

Упражнение 6. Постройте треугольник, задаваемый системой неравенств
Найдите координаты его вершин.
Решение. Точка A — точка пересечения прямых y = 2x – 3 и y = x + 1. Для нахождения координат точки A составим и решим систему уравнений.
Для точки A:  Точка A(4; 5).
Точка A(4; 5).
Для точки B: Точка B(2; 1).
Для точки C: Точка C(–0,5; 0,5).
Упражнение 7. При каких значениях параметра k система неравенств задает на координатной плоскости треугольник?
Упражнение 8. В двух ящиках находится более 29 одинаковых деталей. Число деталей в первом ящике, уменьшенное на 2, более чем в три раза превышает число деталей во втором ящике. Утроенное число деталей в первом ящике превышает удвоенное число деталей во втором ящике менее чем на 60. Сколько деталей в каждом ящике?
Решение. Пусть в первом ящике x деталей, а во втором — y (заметим, что x и y по смыслу задачи — натуральные числа). Составим систему неравенств по условию задачи:
Изобразим на координатной плоскости множество решений системы. Заметим, что в полученной области только одна точка имеет целочисленные координаты. Значит, x = 24, y = 7.
Ответ: 24 детали в первом, 7 деталей во втором ящике.
Задание на дом
1. Изобразите множество точек координатной плоскости, принадлежащих семейству прямых, заданных уравнениями y = (a2 + 1)x.
2. Найдите целочисленные решения системы неравенств
3. Решите неравенство x(x – a)
| Занятие № 15
Решение неравенств с параметрами.
Плоскость Oxa |
Упражнение 1. Найдите площадь треугольника, который задает система неравенств
Упражнение 2. Изобразите на координатной плоскости множество решений системы 
Дальнейшим углублением в тему «Неравенства с двумя переменными» будет рассмотрение неравенств вида F(x; a) ∨ 0, где графики будут строиться в системе координат Oxa. На примере неравенства 3 из домашнего задания рассмотрим аналитический и графический способы решения неравенства. Еще раз обратим внимание учащихся на то, что графический способ удобен, если можно построить график соответствующего уравнения.
Упражнение 3. Решите неравенство x(x – a)
Решение. Способ I (аналитический). Произведение двух множителей отрицательно, если множители имеют разные знаки, отсюда получаем:
Если a — число отрицательное, то решение первой системы — промежуток (a; 0), решение второй системы — пустое множество.
Если a — положительное число, то решение первой системы — пустое множество, а решение второй — промежуток (0; a).
Если a = 0, то неравенство примет вид x2
Способ II (графический). Изобразим решение неравенства в системе координат Oxa. Проведем произвольную прямую a = α, она пересечет заштрихованную часть. Соответствующие значения x и будут являться решением неравенства. По графику нетрудно определить, что при a a; 0), при a = 0 x ∈  , при a 0 x ∈ (0; a).
, при a 0 x ∈ (0; a).
Ответ: при a a; 0);
при a = 0 x ∈  ;
;
при a 0 x ∈ (0; a).
Далее учащиеся самостоятельно решают упражнение 4.
Упражнение 4. Решите неравенство:
а) (x – 2a)(x – a) б) a2 – x2 ≥ (x + a)(4 – a);
в) 
Решение.
а)
Ответ: при a a; 0);
при a = 0 x ∈  ;
;
при a 0 x ∈ (a; 2a).
б) Преобразуем данное неравенство
(a – x)(x + a) ≥ (x + a) (4 – a),
(a – x)(x + a) – (x + a)(4 – a) ≥ 0,
(x + a)(2a – x – 4) ≥ 0.
Изобразим на координатной плоскости множество точек, соответствующих данному неравенству.
Чтобы определить координаты точки пересечения прямых, решим уравнение –x = 0,5x + 2, откуда 
Тогда 
Ответ:
в) Дробь  если числитель и знаменатель имеют разные знаки. Поэтому
если числитель и знаменатель имеют разные знаки. Поэтому
Изобразим множество точек, соответствующих неравенству
Ответ: при a ≤ –2 x ∈ (–∞; a) ∪ (–2; 2);
при –2 a a; 2);
при a ≥ 2 x ∈ (–∞; –2) ∪ (2; a).
Задание на дом
Задание дается по всему курсу. На занятии № 16 планируется защита решений предложенных задач.
| Занятие № 16 Решение задач с параметрами |
Данное занятие рассчитано на повторение и обобщение знаний, полученных учащимися во время знакомства с курсом, и проводится как защита решений задач.
Упражнение 1. При каких значениях параметра b корень уравнения  принадлежит промежутку (–1; 4)?
принадлежит промежутку (–1; 4)?
Решение. Решив уравнение относительно x, получим, что при любых значениях параметра b уравнение имеет один корень:  По условию задачи корень должен принадлежать промежутку (–1; 4), то есть
По условию задачи корень должен принадлежать промежутку (–1; 4), то есть  Решим полученное двойное неравенство:
Решим полученное двойное неравенство:
Ответ: при  корень уравнения принадлежит промежутку (–1; 4).
корень уравнения принадлежит промежутку (–1; 4).
Упражнение 2. Решите уравнение 
а) относительно x;
б) относительно y.
Решение. Преобразуем уравнение 
а) Решим уравнение относительно x:  .
.
Так как x ≠ –1, то y – 1 ≠ –1, то есть y ≠ 0. Итак, если y = 0, то x ∈ ѕ, если y ≠ 0, то x = y – 1.
б) Решим уравнение относительно y: 
Тогда при x = –1 y ∈ ; если x ≠ –1, то y = x + 1.
; если x ≠ –1, то y = x + 1.
Ответ: а) при y = 0 x ∈  ;
;
при y ≠ 0 x = y – 1;
б) при x = –1 y ∈  ,
,
при x ≠ –1 y = x + 1.
Упражнение 3. Найдите точки пересечения с координатными осями графика функции 
Решение. Если точка лежит на оси ординат, то ее абсцисса равна 0. Если x = 0, то 
Итак, точка пересечения графика с осью ординат — (0; –2). У точки, лежащей на оси абсцисс, ордината равна 0, то есть  Данное уравнение равносильно системе
Данное уравнение равносильно системе 
Если a = 0, то первое уравнение системы примет вид 0∙x = 4, и уравнение не имеет корней.
Если a ≠ 0, то первое уравнение имеет единственный корень  Но x ≠ –2, значит, при
Но x ≠ –2, значит, при  то есть a = –2, уравнение
то есть a = –2, уравнение  не имеет корней. Итак, если a = 0 или a = –2, то график не пересекает ось абсцисс, если a ≠ 0 и a ≠ –2, то график пересекает ось абсцисс в точке
не имеет корней. Итак, если a = 0 или a = –2, то график не пересекает ось абсцисс, если a ≠ 0 и a ≠ –2, то график пересекает ось абсцисс в точке 
Ответ: при a = 0 или a = –2 график пересекает только ось ординат в точке (0; –2);
при a ≠ 0 или a ≠ –2 график пересекает ось ординат в точке (0; –2) и ось абсцисс в точке 
Упражнение 4. При каких значениях параметров a и b уравнение (2a – b + 1)x + 2a + b – 3 = 0 имеет не менее двух различных решений?
Решение. Уравнение является линейным относительно переменной x. Оно будет иметь не менее двух различных корней, если при некоторых значениях параметров примет вид 0∙x = 0. Тогда получим систему уравнений

решением которой является пара чисел a = 0,5, b = 2.
Ответ: при a = 0,5, b = 2.
Упражнение 5. При каких значениях параметра b уравнение (a – 3)x = b + 2a имеет корни при любых значениях параметра a?
Решение. Уравнение (a – 3)x = b + 2a может не иметь корней при a = 3. Чтобы и при a = 3 оно имело корни, надо, чтобы оно приняло вид 0∙x = 0.
Решим систему уравнений
Откуда получим: a = 3, b = –6.
Ответ: при b = –6.
Упражнение 6. Решите уравнение (x – a2)(x – | a |) = 0.
Решение. Построим график уравнения (x – a2)(x – | a |) = 0 в координатной плоскости Oxa, где горизонтальная ось — ось a, вертикальная — ось x, прямая a = α в этом случае будет перемещаться слева направо.
Из чертежа видно, что уравнение имеет два корня: x = a2 и x = | a | при a a a a 1, и один корень x = 1 при a = ±1 или x = 0 при a = 0.
Ответ: при a a a a 1 x = a2 и x = | a |;
при a = 0 x = 0;
при a = ± 1 x = 1.
Упражнение 7. Исследуйте количество решений системы уравнений
в зависимости от значений параметра m.
Решение. Решим уравнение 
Тогда
(m – 4)(m + 1) = –2(m + 2), m2 – 3m – 4 = –2m – 4, m2 – m = 0, m = 0 или m = 1.
Рассмотрим пропорцию
При m = 0 получаем: — верно.
Значит, при m = 0 система имеет бесконечно много решений.
Если m = 1, то  — неверно,
— неверно,
значит, при m = 1 система не имеет решений.
Ответ: при m = 0 — бесконечно много решений;
при m = 1 нет решений;
при m ≠ 0 и m ≠ 1 — единственное решение.
Упражнение 8. При каких значениях параметра a неравенство  справедливо для всех x из промежутка [1; 2]?
справедливо для всех x из промежутка [1; 2]?
Решение. Значение дроби отрицательно, если числитель и знаменатель имеют разные знаки. Тогда
Отсюда
Первая система имеет решения, если 2a + 1 a, то есть при a –1. Промежуток [1; 2] не входит во множество решений системы, если 
Решением данной системы является промежуток (0,5; 1).
Вторая система имеет решения, если 2a + 1 a, то есть при a Промежуток [1; 2] входит во множество решений системы, если 
Данная система не имеет решения.
Ответ: при a ∈ (0,5; 1).
Упражнение 9. Решите неравенство:
а) (x – a)2(x – 2a) б) (x – a)2(x – 2a) ≤ 0;
в) | x |(x – a) 0;
г) | x + a |(x – 2) ≥ 0.
Решение. а) Так как (x – a)2 ≥ 0 при любых значениях переменной, то неравенство
(x – a)2(x – 2a) выполняется, если
x – 2a a)2 ≠ 0;
то есть при x a, x ≠ a.
Если 2a a, то есть a 0, то решение неравенства x ∈ (–∞; a) ∪(a; 2a).
Если a ≤ 0, то x ∈ (–∞; 2a).
Ответ: при a 0 x ∈ (–∞; a) ∪ (a; 2a);
при a ≤ 0 x ∈ (–∞; 2a).
б) Так как (x – a)2 ≥ 0 при любых значениях переменной, то неравенство (x – a)2(x – 2a) ≤ 0 выполняется, если x – 2a ≤ 0 или (x – a)2 = 0; то есть при x ≤ 2a или x = a. Если 2a ≥ a, то есть a ≥ 0,
то решение неравенства x ∈ (–∞; 2a], если a a] ∪ {a}.
Ответ: при a ≥ 0 x ∈ (–∞; 2a];
при a a) c {a}.
в) Так как | x | ≥ 0 при любых значениях переменной, то | x |(x – a) 0, если x a, x ≠ 0. Если a ≥ 0, то x ∈ (a; +∞), если a a; 0) ∪ (0; +∞).
Ответ: при a ≥ 0 x ∈ (a; +∞);
при a a; 0) ∪ (0; +∞).
г) Так как | x + a | ≥ 0 при любых значениях переменной, то | x + a |(x – 2) ≥ 0, если x ≥ 2 или
x = –a. Если a –2, то x ∈ [2; +∞) ∪ {–a}, если
a ≤ –2, то x ∈ [2; +∞).
Ответ: при a –2 x ∈ [2; +∞) ∪ {–a};
при a ≤ –2 x ∈ [2; +∞).
Упражнение 10. Решите систему неравенств
двумя способами (аналитическим и графическим с использованием системы координат Oxa).
Решение. Способ I (аналитический).
Чтобы система имела решение, необходимо, чтобы 
откуда a ≥ 1. Если a 1, то 
если a = 1, то x = 1. При a
Способ II (графический). Изобразим в координатной плоскости Oxa множество решений, соответствующих первому и второму неравенству.
Перемещая прямую a = α снизу вверх, получим решения системы неравенств.
Ответ: при a 1 
при a = 1 x = 1; при a
Упражнение 11. Сколько общих точек в зависимости от параметра a имеет график функции
с прямой: а) y = a; б) y = ax?
Решение.
а)
Ответ: при a при a = –2 — две точки;
при –2 a при a = 2 — бесконечное множество точек;
при a 2 общих точек нет.
б)
Ответ: при a a 1 — одна точка;
при a = –1 и a = 1 — две точки;
при –1 a при 0 ≤ a
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Модель профильного обучения включает в себя базовые общеобразовательные и профильные предметы, а также элективные курсы. Функция элективных курсов – реализация личностно-ориентированного учебного процесса, позволяющего учитывать интересы, склонности и способности учащихся и создавать условия для обучения старшеклассников в соответствии с их профессиональными интересами и намерениями в отношении продолжения образования.
Необходимость введения курса «Решение задач с параметром» обусловлена тесной взаимосвязью таких задач с физическими процессами и геометрическими закономерностями, включением их в задания олимпиад, конкурсов, ЕГЭ.
Практика работы в школе показывает, что уравнения и неравенства с параметром - это один из сложнейших разделов школьного курса математики, представляющий для школьников наибольшую трудность, как в логическом, так и в техническом плане. Решение уравнений и неравенств с параметрами можно считать деятельностью, близкой по своему характеру к исследовательской. Выбор метода решения, запись ответа совершенствуют умения наблюдать, сравнивать, анализировать, строить схемы и графики, выдвигать гипотезу и обосновывать полученные результаты. Задачи с параметром проверяют не только умение работать по алгоритму, но и способность к поиску нестандартных решений, формируя при этом творческий подход к выполнению заданий.
Данный элективный курс «поддерживает» изучение профильного предмета, выстраивает индивидуально-образовательную траекторию учащегося, а такжепозволяет сократить разрыв между требованиями, предъявляемыми к выпускнику при выполнении заданий итоговой аттестации и школьной программой. В процессе его изучения учащиесязнакомятсяс методами решения задач с параметром (аналитическим, функциональным, функционально-графическим), приобретают навыки рационального поиска решения, открывают перед собой эвристические приемы, ценные для математического развития личности.
Цель курса:
создание базы математических знаний, умений и навыков, способствующих рациональному решению задач с параметром;
приобщение учащихся к творческой и исследовательской деятельности, обеспечивающей в будущем интеллектуальную и социальную самореализацию;
формирование представлений о значимости математики как инструмента познания окружающего мира и двигателя научно-технического прогресса.
Задачи курса:
формирование у учащихся навыков решения уравнений и неравенств с параметром различными способами;
стимулирование исследовательской деятельности школьников;
формирование логического и творческого мышления учащихся;
повышение математической культуры;
развитие устойчивого интереса учащихся к изучению математики;
подготовка к итоговой аттестации и продолжению образования.
Элективный курс предполагает включение в содержание программы теоретического и практического материала. Теоретическая часть содержит упорядоченные сведения об уравнениях и неравенствах с параметром, способы их решения и обоснование, а практическая – задачи различных типов, разного уровня сложности, предназначенные для индивидуальной, парной, групповой и коллективной форм работы. Значительное место отводится самостоятельной математической деятельности учащихся – решению задач, проработке теоретического материала, подготовке сообщений, презентаций. Особое внимание на занятиях уделяется организации научно-исследовательской деятельности учащихся и формированию у них умения конструировать задания.
Методы, применяемые на занятиях, подобраны в соответствии с содержанием курса, особенностями тематики и органично сочетают лекции, семинары, практикумы.
В процессе преподавания элективного курса важным компонентом являются средства обучения:
печатные пособия (учебники, раздаточный и дидактический материалы);
наглядные пособия (плакаты, графики, таблицы);
электронные образовательные ресурсы (мультимедийные средства обучения).
При планировании элективного курса учтена возможность включения разнообразного иллюстративного материала, мультимедийных и интерактивных моделей, использование компьютерной информационной базы для организации самостоятельной работы школьников при повторении теоретического материала и тестирования для проверки и контроля знаний.
Специфика работы учителя во многом определяется уровнем подготовки учащихся, их способностями, а самое главное – их мотивацией. Поэтому в программе даны варианты заданий, для решения которых потребуется различный уровень знаний и умений. В зависимости от темы занятия педагог выступает как информатор, консультант, наблюдатель, эксперт или занимает позицию активного участника учебного процесса.
Программа курса разработана для классов естественно-математического, социально-экономического профилей в старшей школе и предназначена для организации систематического изучения вопросов, связанных с параметром. Элективный курс продолжительностью 34 часа рассчитан на учащихся 11-х классов, обладающих достаточной математической подготовкой, проявляющих интерес к предмету, и желающих овладеть различными умениями, навыками и приемами для решения математических задач с параметром.
Элективный курс «Решение задач с параметром» соответствует:
МЕТОДИЧЕСКАЯ ЧАСТЬ
Преподавание элективного курса строится как углубленное изучение вопросов, предусмотренных программой основного курса. Углубление реализуется на базе обучения методам и приемам решения математических задач, требующих применения высокой логической и операционной культуры, развивающих научно-теоретическое, алгоритмическое и творческое мышление, и позволяет школьникам научиться решать задачи повышенной сложности.
В процессе преподавания элективного курса используются технологии, ориентированные на получение учащимися практики, позволяющей овладеть общеучебными умениями и навыками для успешного усвоения программы профильной школы. Активную учебно-познавательную деятельность, направленную на личностное развитие каждого ученика, формирование и развитие ключевых и предметных компетенций школьников обеспечивает применение:
лекционно-семинарской системы обучения;
информационно-коммуникационных технологий;
дифференцированного обучения;
исследовательского метода в обучении;
проблемного обучения;
технологии деятельностного метода, позволяющей выявлять познавательные интересы и способности школьников;
личностно-ориентированого обучения.
В результате изучения курса учащиеся приобретут умения:
описывать реальные ситуации с помощью математических моделей;
анализировать и выбирать оптимальные способы решения уравнений и неравенств с параметром;
отстаивать своё мнение по выбору способа решения нестандартных задач с параметром;
применять свойства функций для построения графиков и решения уравнений и неравенств с параметром;
строить и читать графики функций;
логически мыслить, рассуждать, выдвигать гипотезы, делать выводы, обосновывать полученные результаты;
работать с различными источниками информации.
Результат обучения выражается в повышение математической культуры, в проявлении умения осуществлять исследовательскую деятельность и применять полученные знания для решения практических задач.
Оценка качества деятельности обучающегося проводится методом модульно-рейтинговой системы контроля достижений. Качество знаний учащихся обеспечивается регулярностью их работы в течение всего периода обучения. Текущие оценки переводятся учителем в баллы и складываются в итоговый показатель качества освоения курса. За выполнение индивидуальных работ в форме сообщений, докладов, рефератов и заданий повышенной сложности ученики получают дополнительные баллы.
Отчётность по освоению курса предусматривает проверку домашних заданий, самостоятельных работ, тестов, оценивание качества исследовательских проектов. По итогу курса проводится защита групповых и индивидуальных заданий исследовательского типа, рефератов и творческих работ.
Литература:
Ильясов И. И. Структура процесса учения — М.: 1986.
Махмутова М. И. Современный урок — М.: 1981.
Пидкасистый П. И. Педагогика — М.: 2004.
Прессман Л. П. Методика и техника эффективного использования средств обучения в учебно-воспитательном процессе — М.: 1985.
Профильное обучение: программы элективных курсов здоровьесберегающей направленности: Учебно-методическое пособие / Под ред. Т.В. Черниковой. – М.: ТЦ Сфера, 2006. – 304 с. (Педагогическое мастерство).
Скаткин М. Н. Совершенствование процесса обучения — М.: 1971.
Содержание курса 1. Начальные представления о параметре (0,5 ч.) Вводная беседа. Назначение, структура и краткое содержание учебного курса. Понятие параметра, уравнения и неравенства с параметром.
2. Способы решения задач с параметром (3,5 ч.) Знакомство со способами решения уравнений и неравенств с параметром (аналитическим, функциональным и функционально-графическим), рассмотрение общих схем и закономерностей в поиске решений. Систематизация задач по типу ограничений, накладываемых на параметр. Графическая интерпретация задач с параметром: построение графического образа на координатной плоскости (хОу) и на плоскости (хОа). Сочетание графического и алгебраического методов решения уравнений. Сравнительный анализ аналитического, функционально-графического способов при решении уравнений и неравенств с параметром.
Практическая работа №1
«Определение типа задач с параметром и выстраивание схемы поиска решения»
3. Задачи с параметром (17 ч.) Приемы решения рациональных, иррациональных, тригонометрических, показательных и логарифмических уравнений, неравенств и систем с параметром. Рассмотрение уравнений и неравенств, содержащих различные функции. Выбор оптимального метода решения.
Практическая работа №2
«Решение задач с параметром с выбором рационального способа решения»
4. Комбинированные задачи с модулем и параметром (4 ч.) Комбинированные задачи с модулем и параметром. Обобщенный метод областей. Перенос метода интервалов с прямой на плоскость. Нахождение площади фигур, ограниченных неравенством. Применение метода областей к решению уравнений и неравенств с параметром и модулем, и их комбинации.
Практическая работа №3
«Решение задач с модулем и параметром с выбором рационального способа решения»
5. Конструирование задач с параметром (2 ч.) Технология конструирования задач с параметром. Использование графиков различных соответствий и уравнений. Демонстрация приёма составления задач с параметром методом «от картинки к задаче».
Практическая работа №4 «Конструирование задач с параметром»
6. Задачи единого государственного экзамена (5 ч.) Нетрадиционные задачи с параметром. Практикум по решению задач, относящихся к группе «С», входящих в контрольно измерительные материалы ЕГЭ прошлых лет. Анализ методов решения заданий. Использование экстремальных свойств рассматриваемых функций. От общего к частному и обратно.
7. Защита рефератов и творческих работ (2 ч.) Выступления учащихся с рефератами по различным вопросам темы, практическому применению задач с параметрами, проблемам организации эффективной деятельности при решении математических задач разных типов и вопросам саморегуляции. Защита творческих работ и демонстрация презентаций.
В учебно-методический комплект включены:
учебно-тематический план курса (приложение 1);
практические работы для закрепления знаний учащихся и отработки навыков решения задач с параметром (приложение 2);
разработки занятий по темам «Функционально-графический способ решения задач с параметром» (приложение 3) и «Конструирование задач с параметром» (приложение 4) с методическими рекомендациями по их проведению;
мультимедийные средства обучения: демонстрационный материал и устный счёт по темам «Аналитический способ решения задач с параметром», «Функционально-графический способ решения задач с параметром», «Технология конструирования задач с параметром», «Задачи единого государственного экзамена» (презентации 1-6);
комплекс задач с параметром, рекомендуемый к возможному использованию в учебном процессе для формирования навыков решения уравнений, неравенств и систем функционально-графическим способом (приложение 5);
самостоятельные работы по темам «Линейные уравнения, неравенства с параметром», «Квадратные уравнения и неравенства с параметром», «Тригонометрические уравнения с параметром» для организации промежуточного контроля знаний учащихся и ответы к заданиям (приложение 6).
Список литературы для педагога:
Вавилов В.В., Мельников И.И., Олехник С.Н., Пасиченко П.И. Задачи по математике. Уравнения и неравенства. Справочное пособие. – М.: Наука; 1987.
Горнштейн П.И., Полонский В. Б., Якир М.С. Задачи с параметрами. – М: Илекса, 2007., 326 с.
Дворянинов С.В., Письменная С.А. «Функции, графики, задачи с параметром». Самара, 1998.
Джиоев Н.Д. Нахождение графическим способом числа решений уравнений с параметром. Математика в школе – 1996. - №2. – С. 54-57.
Кожухова, С.А. Свойства функций в задачах с параметром. Математика в школе – 2006. - №7. – С. 17-24.
Кочерова, К.С. Об уравнениях с параметром и модулем (графический способ решения). Математика в школе – 1995. - №2. – С. 2-4.
Кушнир И. Шедевры школьной математики. 1,2 том «АСТАРТА», Киев, 1995. 573с., 509с.
Максютин А.А. Математика 10. Индивидуальные домашние задания по алгебре, началам анализа и геометрии. ЗАО «Папирус», Самара, 2002 г., 588 с.
«Математика 5 – 11 классы. Практикум», учебное электронное издание, компакт – диск для работы на компьютере.
Мещерякова Г.П. Функционально-графический метод решения задач с параметром Математика в школе – 1999. - №6. – С. 69-71.
Саханевич М. ЕГЭ: решение сложных задач. Математика. Издательский дом «Первое сентября», № 12, 2004.
Ястребицкий Г.А. Уравнения и неравенства, содержащие параметры: пособие для учителей. М: Просвещение, 1972.
www.spin.nw.ru/student/dist_ed/math_problem1.htm
Список литературы для учащихся:
Балаян Э.Н. Математика. Сам себе репетитор. Задачи повышенной сложности. Серия «Абитуриент», Ростов на – Дону: Изд-во «Феникс», 2004.
Колесникова С.И. Математика. Решение сложных задач Единого государственного экзамена. – 3-е изд. – М.: Айрис-пресс, 2007. – 272 с. – (Домашний репетитор Подготовка к ЕГЭ).
Локоть В.В. Задачи с параметрами. Линейные и квадратные уравнения, неравенства, системы: Учебное пособие. – 2-е изд., испр. и доп. – М.: АРКТИ, 2005. – 96 с. (Абитуриент).
Локоть В.В. Задачи с параметрами. Иррациональные уравнения, неравенства, системы, задачи с модулем. – 2-е изд., испр. и доп. – М.: АРКТИ, 2006. – 64 с. (Абитуриент: Готовимся к ЕГЭ).
Локоть В.В. Задачи с параметрами. Показательные и логарифмические уравнения, неравенства, системы. – 2-е изд., испр. и доп. – М.: АРКТИ, 2005. (Абитуриент: Готовимся к ЕГЭ).
«Математика абитуриенту. Версия 2.0.: «1145 задач по математике», компакт – диск для работы на компьютере.
Моденов В.П. Задачи с параметрами. Координатно-параметрический метод. Учебное пособие для школьников и абитуриентов. ООО «Экзамен» 2007 г, 288 с.
Под редакцией А.И. Прилепко «Сборник задач по математике для поступающих в вузы». М., 1989.
«Репетитор: Математика, часть 1», компакт – диск для работы на компьютере.
Скорикова Л.А. Математика 10 – 11 класс. Задачи с параметром. Волгоград. Учитель, 2010, 166 с.
Цыганов Ш.И. Все задачи ЕГЭ по математике прошлых лет: Учебное пособие, - 4 издание, дополненное – Уфа: Центр педагогических измерений, 2008 г.
Шабунин М.И. «Пособие по математике для поступающих в вузы». М., 1999.
Шарыгин И. Ф. Факультативный курс по математике: Решение задач: Учебное пособие для 10 класса средней школы. – М.: Просвещение, 1989. - 252 с.
Черкасов О.Ю., Якушев А.Г. «Математика: интенсивный курс подготовки к экзамену». – 6-е изд., испр. и доп. – М.: Рольф, 2002. – (Домашний репетитор)
Ястребицкий Г.А. Задачи с параметром. М: Просвещение, 1986.






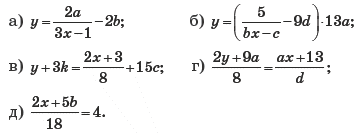
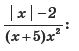
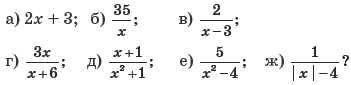
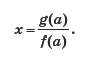

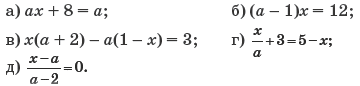
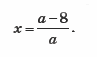
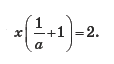
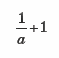 не имеет смысла. Значит, уравнение не имеет корней.
не имеет смысла. Значит, уравнение не имеет корней.