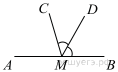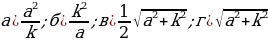РЕЕСТР
ФОНДА ОЦЕНОЧНЫХ СРЕДСТВ ПО ГЕОМЕТРИИ
НА I КУРСЕ
| № | Формы контроля | Тема | Дата | Всего |
| П | Ф |
|
1 четверть
|
| 1 | Контрольная работа | Контрольная работа «Подобие фигур»
|
|
| 1 ч. |
|
2 четверть
|
| 2 | Контрольная работа | Промежуточная аттестация | |
| 1 ч.
|
|
3 четверть
|
| 3 | Контрольная работа | Контрольная работа по теме «Площади фигур» |
|
| 1 ч. |
|
4 четверть
|
| 4 | Итоговая контрольная работа | Итоговая диагностическая работа |
|
| 1 ч. |
| Итого |
|
|
|
| 4 ч. |
Контрольная работа «Подобие фигур»
Вариант 1
Задание 1.
Дано: ∠A = ∠B, СО = 4, DO = 6, АО = 5.
Найти: а) ОВ, б) АС, BD: в) SAOC, SBOD.
Задание 2.
В треугольнике АВС АВ = 4 см, ВС = 7 см, АС = 6 см, а в треугольнике MNK МК = 8 см, MN = 12 см, KN = 14 см. Найдите углы треугольника MNK, если ∠A = 80°, ∠B = 60°.
Задание 3. Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК||АС, ВМ : AM = 1 : 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см.
Задание 4. В трапеции ABCD (AD и ВС основание) диагонали пересекаются в точке О, AD = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника AOD равна 45 см2.
Вариант 2
Задание 1. Дано: РЕ||NK, МР = 8, MN = 12, ME = 6 (рис. 7.55). Найти: а) МК; б) РЕ : NK; в) SMPE : SMNK.
Задание 2. В ΔАВС АВ = 12 см, ВС = 18 см, ∠В = 70°, а в ΔMNK MN = 6 см, NK = 9 см, ∠N = 70°. Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, ∠K = 60°.
Задание 3. Отрезки АВ и CD пересекаются в точке О так, что ∠ACO = ∠BDO, АО : ОВ = 2:3. Найдите периметр треугольника АСО, если периметр треугольника BOD равен 21 см.
Задание 4. В трапеции ABCD (AD и ВС основания) диагонали пересекаются в точке О, SAOD= 32 см2, SBOC = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см.
Ключи к контрольной работе
| № варианта | 1 | 2 | 3 | 4 |
| Вариант 1 | а) 7,5; б) 2:3; в) 4:9 | 80°, 60°, 40° | 5 | 5 |
| Вариант 2 | а) 9; б) 2 : 3; в) 4 : 9 | 14 см; 60° | 14 | 5 |
Промежуточная аттестация
Вариант 1
Задание 1.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 62°, угол ABC равен 47°. Найдите угол ACB. Ответ дайте в градусах. 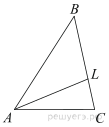
Задание 2.
В остроугольном треугольнике ABC проведена высота BH,  . Найдите угол ABH . Ответ дайте в градусах.
. Найдите угол ABH . Ответ дайте в градусах. 
Задание 3. Биссектриса равностороннего треугольника равна 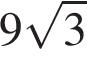 . Найдите сторону этого треугольника.
. Найдите сторону этого треугольника. 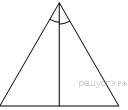
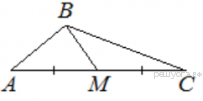
Задание 4. В треугольнике 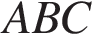 известно, что
известно, что 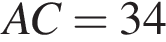 ,
, 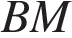 - медиана,
- медиана,  . Найдите
. Найдите  .
.
Задание 5. Прямые m и n параллельны. Найдите ∠3, если ∠1 = 117°, ∠2 = 24°. Ответ дайте в градусах. 
Задание 6. Площадь прямоугольного треугольника равна 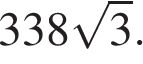 Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.
Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла. 
Задание 7.
На прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 81°. Найдите угол CMA. Ответ дайте в градусах. 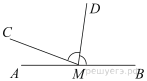
Задание 8.
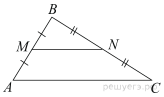
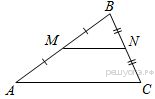
Точки 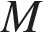 и
и 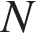 являются серединами сторон
являются серединами сторон 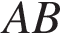 и
и 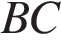 треугольника
треугольника 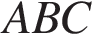 , сторона
, сторона 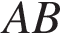 равна 20, сторона
равна 20, сторона 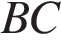 равна 58, сторона
равна 58, сторона 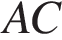 равна 64. Найдите
равна 64. Найдите 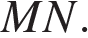
Задание 9. Сторона равностороннего треугольника равна  . Найдите медиану этого треугольника.
. Найдите медиану этого треугольника. 
Задание 10. Медиана равностороннего треугольника равна 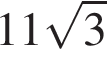 . Найдите сторону этого треугольника.
. Найдите сторону этого треугольника. 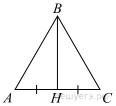
Вариант 2
Задание 1.
Прямые m и n параллельны. Найдите ∠3, если ∠1 = 74°, ∠2 = 39°. Ответ дайте в градусах. 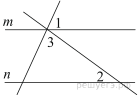
Задание 2.
В треугольнике ABC проведены медиана BM и высота BH. Известно, что AC = 53 и BC = BM. Найдите AH. 
Задание 3.
В треугольнике ABC AB = BC = 65, AC = 50. Найдите длину медианы BM.
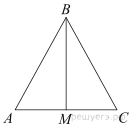
Задание 4. Сторона равностороннего треугольника равна  . Найдите биссектрису этого треугольника.
. Найдите биссектрису этого треугольника. 
Задание 5.
На прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 60°. Найдите угол CMA. Ответ дайте в градусах. 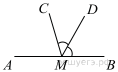
Задание 6.
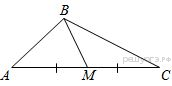
В треугольнике 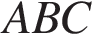 известно, что
известно, что 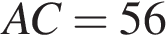 ,
,  - медиана,
- медиана,  . Найдите
. Найдите  .
.
Задание 7.
На прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 48°. Найдите угол CMA. Ответ дайте в градусах. 
Задание 8.
В треугольнике два угла равны 36° и 73°. Найдите его третий угол. Ответ дайте в градусах.
Задание 9.
Медиана равностороннего треугольника равна 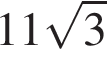 . Найдите сторону этого треугольника.
. Найдите сторону этого треугольника. 
Задание 10.
Точки  и
и 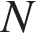 являются серединами сторон
являются серединами сторон 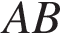 и
и 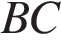 треугольника
треугольника 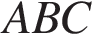 , сторона
, сторона 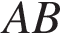 равна 95, сторона
равна 95, сторона 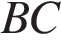 равна 80, сторона
равна 80, сторона 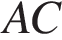 равна 128. Найдите
равна 128. Найдите 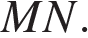
Ключи к промежуточной аттестации
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вариант 1 | 103 | 42 | 18 | 17 | 39 | 26 | 18 | 32 | 24 | 22 |
| Вариант 2 | 67 | 39,75 | 60 | 24 | 60 | 28 | 84 | 71 | 22 | 64 |
Контрольная работа «Площади фигур»
Вариант 1
Задание 1. Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 11 и 14. Найдите длину основания BC. 
Задание 2. В ромбе сторона равна 10, одна из диагоналей равна 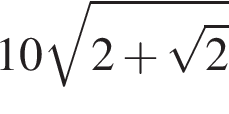 , а угол, лежащий напротив этой диагонали, равен 135°. Найдите площадь ромба, деленную на
, а угол, лежащий напротив этой диагонали, равен 135°. Найдите площадь ромба, деленную на 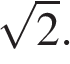
Задание 3. Найдите площадь кругового сектора, если радиус круга равен 3, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.
Задание 4. Площадь прямоугольного треугольника равна  Один из острых углов равен 60°. Найдите длину катета, прилежащего к этому углу.
Один из острых углов равен 60°. Найдите длину катета, прилежащего к этому углу. 
Задание 5. Найдите площадь прямоугольника, если его периметр равен 102, а отношение соседних сторон равно 2:15.
Задание 6. Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 31. Найдите площадь этого треугольника.
Вариант 2
Задание 1. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
Задание 2. Площадь параллелограмма ABCD равна 144. Точка E — середина стороны AD. Найдите площадь трапеции AECB. 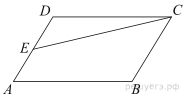
Задание 3. Основания трапеции равны 4 и 14, одна из боковых сторон равна  , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
, а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
Задание 4. Найдите площадь квадрата, если его диагональ равна 20. 
Задание 5. В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 97. Найдите площадь четырёхугольника ABMN. 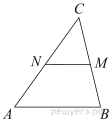
Задание 6. В равнобедренном треугольнике боковая сторона равна 10, основание равно 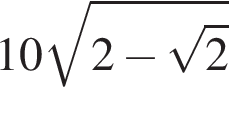 , а угол, лежащий напротив основания, равен 45°. Найдите площадь треугольника, деленную на
, а угол, лежащий напротив основания, равен 45°. Найдите площадь треугольника, деленную на 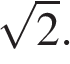
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| Вариант 1 | 3 | 50 | 3 | 2 | 270 | 217 |
| Вариант 2 | 1344 | 108 | 36 | 200 | 291 | 25 |
Ключи к контрольной работе
Итоговая контрольная работа
Вариант 1
Часть I
При выполнении заданий 1-5 выберите верный ответ.
Треугольник со сторонами 5, 9, 15: а) остроугольный; б) тупоугольный; в) прямоугольный; г) такого треугольника не существует.
Если одна из сторон треугольника на 3 см меньше другой, высота делит третью сторону на отрезки 5 см и 10 см, то периметр треугольника равен:
а) 25 см; б) 40 см; в) 32 см; г) 20 см.
Если один из углов ромба равен 60°, а диагональ, проведенная из вершины этого угла, равна 4√3 см, то периметр ромба равен:
а) 16 см; б) 8 см; в) 12 см; г) 24 см.
Величина одного из углов треугольника равна 20°. Найдите величину острого угла между биссектрисами двух других углов треугольника.
а) 84°; б) 92°; в) 80°; г) 87°.
В треугольнике АВС сторона а = 7, сторона b = 8, сторона с = 5. Вычислите ∠A.
Часть II
При выполнении заданий 6-10 запишите подробное решение.
В равнобедренном треугольнике боковая сторона делится точкой касания со вписанной окружностью в отношении 8:5, считая от вершины, лежащей против основания. Найдите основание треугольника, если радиус вписанной окружности равен 10.
В треугольнике ВСЕ ∠C = 60°, СЕ : ВС = 3 : 1. Отрезок СК — биссектриса треугольника. Найдите КЕ, если радиус описанной около треугольника окружности равен 8√3.
Найдите площадь треугольника КМР, если сторона КР равна 5, медиана РО равна 3√2, ∠KOP = 135°.
Диагонали равнобедренной трапеции перпендикулярны. Найдите площадь трапеции, если ее средняя линия равна 5.
Окружность, центр которой лежит на гипотенузе АВ прямоугольного треугольника АВС, касается катетов АС и ВС соответственно в точках Е и D. Найдите величину угла АВС (в градусах), если известно, что АЕ = 1, BD = 3. а) 120°; б) 45°; в) 30°; г) 60°.
Вариант 2
Часть I
При выполнении заданий 1-5 выберите верный ответ.
Треугольник со сторонами 15, 9, 12: а) остроугольный; б) тупоугольный; в) прямоугольный; г) такого треугольника не существует.
Если сходственные стороны подобных треугольников равны 2 см и 5 см, площадь первого треугольника равна 8 см2, то площадь второго треугольника равна: а) 50 см2; б) 40 см2; в) 60 см2; г) 20 см2.
Если в равнобедренном треугольнике длина основания равна 12 см, а его периметр равен 32 см, то радиус окружности, вписанной в треугольник, равен: а) 4 см; б) 3 см; в) 6 см; г) 5 см.
В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 см и 12 см. Найдите катеты треугольника.
а) 12 см и 16 см; б) 7 см и 11 см; в) 10 см и 13 см; г) 8 см и 15 см.
Стороны прямоугольника равны а и k. Найдите радиус окружности, описанной около этого прямоугольника.
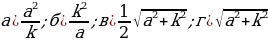
Часть II
При выполнении заданий 6-10 запишите подробное решение.
Окружность с центром О, вписанная в равнобедренный треугольник АВС с основанием АС, касается стороны ВС в точке К, причем СК : ВК = 5 : 8. Найдите площадь треугольника, если его периметр равен 72.
Около треугольника АВС описана окружность. Медиана треугольника AM продлена до пересечения с окружностью в точке К. Найдите сторону АС, если AM = 18, МК = 8, ВК = 10.
Найдите основание равнобедренного треугольника, если угол при основании равен 30°, а взятая внутри треугольника точка находится на одинаковом расстоянии, равном 3, от боковых сторон и на расстоянии 2√3 от основания.
Пусть М — точка пересечения диагоналей выпуклого четырехугольника ABCD, в котором стороны АВ, AD и ВС равны между собой. Найдите угол CMD (в градусах), если известно, что DM = МС, а угол САВ не равен углу DBA.
На боковой стороне ВС равнобедренного треугольника АВС как на диаметре построена окружность, пересекающая основание этого треугольника в точке D. Найдите квадрат расстояния от вершины А до центра окружности, если AD = √3, а угол АВС равен 120°.
Ключи к контрольной работе
|
| Часть 1 | Часть 2 |
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вариант 1 | г | б | а | в | г | 30 | 18 | 3 | 25 | 30 |
| Вариант 2 | в | а | б | г | в | 240 | 15 | 24 | 120 | 7 |