| 4. С формулой суммы n первых членов арифметической прогрессии связан эпизод из жизни немецкого ученого Карла Гаусса. Это было в 18 веке. Существует предание о маленьком вундеркинде Карле Гауссе, будущем немецком математике, решившем в третьем классе очень быстро задачу о нахождении суммы чисел от 1 до 100. Учитель математики должен был уйти и дал задание учащимся: Найти сумму чисел от 1 до 100.Но не успел он уйти, как один мальчик поднял руку и дал ответ-5050. -Как же ты это сосчитал?- спросил учитель -Очень просто- ответил мальчик- я сложил 1 и 100 получил 101, потом сложил 2 и 99 снова получи 101 и т .д. 1 + 2 + 3 +…+ 98 + 99 + 100 = S. 100 + 99 + 98 +…+ 3 + 2 + 1 = S 101 + 101 + 101 +… + 101 +101 +101 = 2 S; 101 · 100 = 2 S; S = 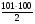 = 5050. = 5050.
Нужно сложить 101 50 раз,т.е 101* 50= 5050. Изумлённый учитель понял , что встретил самого способного ученика в своей жизни. Это был Иоганн Фридрих Карл Гаусс.
Теорема Сумма первых n членов арифметической прогрессии равна полусумме крайних членов, умноженной на число членов . 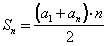 Тренировочные упражнения: (an) – арифметическая прогрессия. a1 = 6, a5 = 26. Найти S5.
Решение: Sn = (а1+а5) : 2 × 5 Теперь вычислим сумму пяти первых членов арифметической прогрессии: S5 = (6+26) : 2 × 5=80. Ответ: 80. (an) – арифметическая прогрессия. a1 = 12, d = - 3. Найти S16. Решение: S16 = (а1+а16):2×16 Заметим, что в данной прогрессии не задан последний член этой суммы. Найдем 16 член прогрессии: а16 = 12+ 15×(-3) =12+(-45) =-33 Теперь вычислим сумму: S16 = (12+ (-33)) ×16: 2 = (-21) ×8 = -168. Ответ: -168. При решении таких задач можно воспользоваться второй формулой для нахождения Sn.
| 






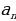 )
)
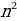 +n;
+n; 









