рисунке изображена схема метро в городе N. Станция Ветреная расположена между станциями Центральная и Дальняя. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя, Птичья и Веселая. Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звездная. Всего в метрополитене города N есть три станции, от которых тоннель ведет только в одну сторону – это станции Дальняя, Верхняя и Звездная. Максим живет недалеко от станции Надежда.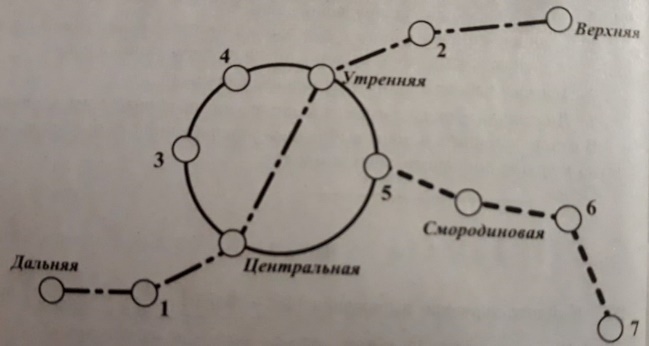
Задание №1
Для станций, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность четырех цифр.
Решение: для того, чтобы правильно определить номера станций, необходимо при чтении информации выделять (подчеркивать) их как в тексте, так и сразу же подписывать на рисунке. Ниже показана часть текста, в которой подчеркнуты основные моменты, а также расстановка станций, которая выполняется сразу по ходу чтения текста.
Станция Ветреная расположена между станциями Центральная и Дальняя (значит, это номер 1). Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя (сразу видно, что двигаться надо от Центральной к Утренней, значит, Быстрая будет под номером 5), Птичья и Веселая (соответственно 4 и 3, так как двигаемся по кольцу). Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звездная (видим эту ветку справа нижнюю, соответственно Хоккейная – номер 6, а Звездная – 7). Максим живет недалеко от станции Надежда (она под номером 2, так как осталась одна не указанная).
Теперь расставляем номера необходимых объектов в таблицу:
В бланк записываем ответ: 6241
Задание №2
Бригада меняет рельсы на участке между станциями Надежда и Верхняя протяженностью 8 км. Работы начались в понедельник. Каждый рабочий день бригада меняла по 500 метров. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?
Решение: для того, чтобы узнать, сколько дней был закрыт проезд, нужно узнать, сколько рабочих дней они прокладывали рельсы. По условию длина участка 8 км, переводим ее в метры, так как в 1 день меняли по 500 метров. Получаем 8000 метров. Теперь делим 8000 метров на 500 метров, получаем 16 рабочих дней трудилась бригада. Нам надо узнать, сколько дней всего был закрыт проезд, так как в выходные работ не было, а проезд был закрыт. По условию работы начались с понедельника, значит бригада работала 3 полных недели и 1 понедельник на четвертой неделе (16 дней делим на 5 рабочих в неделю, получается 3 недели и 1 остается – понедельник). После каждой недели у нас два дня выходных: 2 после первой, 2 после второй, 2 после третьей. Таким образом, 6 выходных был закрыт проезд. Значит, 16 рабочих и 6 выходных, это 22 полных дня был закрыт проезд.
Записываем ответ 22 в бланк.
Задание №3
Территория, находящаяся внутри кольцевой линии, называется Центральным городским районом. Найдите его площадь S (в квадратных километрах), если длина кольцевой ветки равна 32 км. В ответе укажите S*.
Решение: так как известна длина кольцевой ветки, то это значит, что мы имеем длину окружности (по условию – кольцевая ветка – это окружность). Длина окружности вычисляется по формуле 2πR. Значит, 2πR=32. Делим обе части на 2, получаем πR=16. Находим радиус, для этого надо 16 разделить на число π. То есть R=16/π. Формула площади круга S=πR2. Подставляем в нее вместо радиуса 16/π. Получаем, что S=π(16/π) 2. Возводим в квадрат, получаем S=π(256/π2). Теперь сокращаем числитель и знаменательна число π. Получается, что S=256/π . Поскольку в задании есть указание, что в ответ надо записать S* , то умножая эти величины в нашей формуле S=256/π, получаем, что S*= 256. Записываем ответ 256 в бланк.
Задание №4
Найдите расстояние (по железной дороге) между станциями Смородиновая и Хоккейная, если длина Радужной ветки равна 14 км, расстояние от Звездной до Смородиновой 11 км, а от Быстрой до Хоккейной – 7 км. Все расстояния даны по железной дороге.
Решение: итак, Радужная ветка – это станции Быстрая, Смородиновая, Хоккейная и Звездная. Можно для удобства сделать чертеж и обозначить на нем станции первыми буквами их названий и расставить длины. Получится вот такой рисунок, по которому можно легко определить расстояние от Смородиновой (С) до Хоккейной (Х).
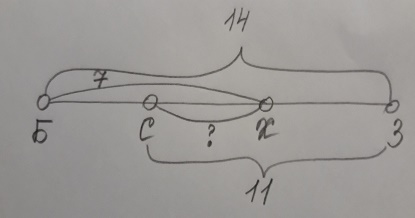
Для этого из длины отрезка СЗ=11 нужно вычесть длину отрезка БХ=7, получим длину СХ=4. В бланк записываем число 4.
Задание №5
Школьник Максим в среднем за месяц совершает 45 поездок на метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. По истечении месяца Максим уедет из города к бабушке в деревню и неиспользованные карточки обнулятся. Во сколько рублей обойдется самый дешевый вариант?
| Количество поездок | Стоимость одной поездки (в рублях) | Дополнительные условия |
| 1 | 40 | Школьникам скидка 20% |
| 10 | 37 | Школьникам скидка 10% |
| 30 | 35 | Школьникам скидка 10% |
| 50 | 32 | Нет |
| Безлимит | — | Любое число поездок в течение месяца за 2000 рублей |
Решение: для решения этого задания необходимы данные только из таблицы. Итак, нужно совершить 45 поездок за наименьшую стоимость. Значит, два последних варианта не подходят, так как 50 поездок – это много, деньги на карте обнулятся, а по Безлимиту в среднем приблизительно выйдет одна поездка 44 рубля (2000 : 45 поездок), скидки здесь не предусмотрены. Следовательно, будем составлять наборы из первых трех вариантов, а затем выбирать самый дешевый.
Для удобства надо посчитать каждый из трех вариантов, как карточку для школьника, т.е. с указанной скидкой. Затем посчитать стоимость каждой карточки полностью. Вспомним, чтобы найти количество процентов от данного числа, надо число разделить на 100 и умножить на количество процентов. Запишем это решение в таблице.
| Количество поездок | Стоимость одной поездки (в рублях) | Стоимость одной поездки для школьника (в рублях) | Стоимость 1 карточки для школьника (в рублях) |
| 1 | 40 | 40-40:100*20=32 | 1*32=32 |
| 10 | 37 | 37-37:100*10=33,3 | 10*33,3=333 |
| 30 | 35 | 35-35:100*10=31,5 | 30*35=945 |
Допустим, что можно купить из первого варианта 45 карточек по 32 руб. Тогда получим, что 32*45=1440 руб.
Допустим, что можно купить на 45 поездок: одну третью (на 30 поездок), 1 вторую (на 10 поездок) и пять первых (на пять поездок). Рассчитаем стоимость.
Одна третья карточка на 30 поездок – это 945 рублей.
Одна вторая карточка на 10 поездок – это 333 рубля.
Пять первых карточек: 32*5=160 рублей.
Теперь складываем стоимость всех карточек. 945+333+160=1438 рублей. Это уже меньше, чем в решении 1.
Допустим, что можно купить 1 третью карточку (на 30 поездок) и 15 первых, так как это тоже 45 поездок. Одна третья карточка на 30 поездок – это 945 рублей. 15 первых будут стоить 15*32=480 рублей. Складываем стоимости 945 и 480, получаем 1425 рублей.
Допустим, что можно еще купить 4 вторых (на 40 поездок) и 5 первых карточек. Тогда 4*333=1332 руб; 5*32=160 руб. Вместе это составит 1332+160=1492 рубля.
Записываем в ответ число 1425, так как это самый дешевый вариант из всех.
Ответ: см. в решении
В горных районах, особенно в южных широтах с влажным климатом, земледельцы на склонах гор устраивают террасы. Земледельческие террасы – это горизонтальные площадки, напоминающие ступени. Во время дождя стекает с верхних террас вниз по специальным каналам. Поэтому почва на террасах не размывается и урожай не страдает. Медленный сток воды с вершины склона вниз с террасы на террасу позволяет выращивать даже влаголюбивые культуры. В Юго-Восточной Азии террасное земледелие широко применяется для производства риса, а в Средиземноморье – для выращивания винограда и оливковых деревьев. Возделывание культур на террасах повышает урожайность, но требует большого ручного труда.

Земледелец владеет несколькими участками, один из которых расположен на склоне холма. Ширина участка 30 м, а верхняя точка находится на высоте 5 м от подножия.

Задание №1. Земледелец на расчищенном склоне холма выращивает мускатный орех. Какова площадь, отведенная под посевы? Ответ дайте в квадратных метрах.
Решение
Мускатный орех земледелец выращивает на склоне холма. Если смотреть на геометрический рисунок, где 5 метров – это высота холма, 30 метров – ширина участка, а 12 метров – это расстояние от подножия холма до нижней точки уклона. Таким образом, расчищенным склоном холма является прямоугольник, закрашенный на рисунке серым цветом.
Требуется найти площадь этого прямоугольника. Смотрим, что его ширина 30 м, а длина неизвестна, но она является гипотенузой прямоугольного треугольника с катетами 5 и 12 метров.
Гипотенузу найдем по теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов). Обозначим гипотенузу буквой с и запишем ее нахождение: с2=122+52=144+25=169; так как √169=13, то с=13.
Теперь находим площадь расчищенного склона холма. Для нахождения S прямоугольника надо длину умножить на ширину. То есть имеем, что 13 м – это длина участка, а 30 м – ширина участка, значит S=13∙30=390 м2
В ответ запишем число 390 (наименования в бланк не пишем).
Ответ: 390
Задание №2. Земледелец решил устроить террасы на своём участке (см. рисунок ниже), чтобы выращивать рис, пшено или кукурузу. Строительство террас возможно, если угол склона (уклон) не больше 50% (тангенс угла склона а, умноженный на 100%). Удовлетворяет ли склон холма этим требованиям? Сколько процентов составляет уклон? Ответ округлите до десятых.

Решение
Во-первых, найдем тангенс по рисунку, который нам дан. Вспомним, что тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. Поэтому, в нашем случае это отношение 5 к 12, то есть tq a=512. Умножим это число на 100%, как сказано в условии задачи, и посчитаем: 512×100=41, 666… Нам сказано, что необходимо округлить число до десятых, то есть оставить после запятой одну цифру (десятые доли), применив правило округления. Получим: 41, 666..≈41,7. Мы видим, что угол склона холма не превышает 50%, то есть он удовлетворяет требованиям для строительства террас. Значит, наш ответ 41,7%.
Ответ: 41,7
Задание №3. На сколько процентов сократилась посевная площадь после того, как земледелец устроил террасы? Ответ округлите до десятых.
Решение:
Для ответа на вопрос задания необходимо сравнить две площади – посевную площадь до строительства террас и площадь террас.
Посевная площадь у нас найдена в задании №1, она равна 390 м2.
Требуется найти площадь террас. Надо понять, что она собой представляет. Посмотрим внимательно на рисунок, где изображены террасы («ступеньки» можно их назвать, глядя на рисунок). Если каждую такую «ступеньку» опустить вниз, то они как раз войдут в расстояние 12 м, то есть длина всех террас, отведённых под посевы равна 12 метров. Ширина участка нам известна, она равна 30 метров. Таким образом, мы получили прямоугольник со сторонами 12 и 30 метров, значит, найдем его площадь, что и будет являться площадью террас: 12×30=360 м2.
Вот теперь мы видим, что сначала площадь была 390, а затем она немного уменьшилась и стала равна 360 м2.
Осталось сравнить процентное отношение данных площадей.
Это можно сделать двумя способами.
1 способ: запишем условие для решения, помня, что первоначальная площадь равна 100%.
390 м2 – 100%
360 м2 – х%
Найдем, сколько процентов стала площадь террас: х= 360×100:390=92,307… Так как нам сказано в условии, что ответ надо будет округлить до десятых, то можно это сделать с числом 92,307…: 92,307≈92,3. Помним, что это мы нашли, сколько процентов стала площадь террас. Теперь находим разницу между ними: 100% — 92,3%=7,7%. Её и запишем в ответ.
2 способ: можно решить данную задачу другим способом, имея две площади – 390 м2 и 360 м2. Видим, что площадь уменьшилась на 30 м2, так как 390 – 360 =30.
Значит: 390 м2 – 100%, а 30 м2 — х%. Следовательно х=30×100:390=7,69…%. Округлим до десятых наше число и получим 7,7.
Ответ: 7,7
Задание №4. Земледелец получает 800 г бурого риса с одного квадратного метра засеянной площади. При шлифовке из бурого риса получается белый рис, но при этом теряется 22% массы. Сколько килограммов белого риса получит земледелец со всего своего участка?
Решение:
Смысл данной задачи в том, что земледелец выращивает на террасах бурый рис, затем его обрабатывает и получает белый рис. При обработке масса теряется. Нам надо узнать, сколько кг белого риса он получит со своего участка.
Помним, что рис собирают с террас, площадь которых 360 м2 (мы нашли её в задании 3). Известно, что с 1 м2 собирают 800 г бурого риса, следовательно, чтобы найти, сколько бурого риса он соберет со всего участка площадью 360 м2, надо 800×360, получим 288000 граммов. Переведем граммы в килограммы (это требуется в данной задаче), то есть разделим на 1000, так как 1 кг=1000 г. Значит, 288000:1000=288 кг собирает земледелец бурого риса.
Теперь он его обрабатывает, теряя 22%, значит, из данной массы 288 кг мы должны убрать 22%. Так как 288 кг – это 100%, то после обработки остается 100% — 22%=78%. Переведем 78% в десятичную дробь, получим 0,78. Теперь умножим на 0,78 наши 288 кг, получаем 224,64 кг.
Ответ: 224,64
Задание №5. В таблице дана урожайность культур, которые может засеять земледелец на своем террасированном участке. За год обычно собирают два урожая – летом и осенью. По данным таблицы посчитайте наибольшее число килограммов урожая, которое может собрать земледелец с участка за один год, если он может засевать разные культуры.
|
| Рис | Кукуруза | Пшено |
| 1-ый урожай (июнь) | 600 г/м2 | 1200 г/м2 | Не выращивают |
| 2-ой урожай (сентябрь) | 800 г/м2 | Не выращивают | 300 г/м2 |
Решение:
Итак, подчеркнем в условии для себя, что нам надо найти: В таблице дана урожайность культур, которые может засеять земледелец на своем террасированном участке. За год обычно собирают два урожая – летом и осенью. По данным таблицы посчитайте наибольшее число килограммов урожая, которое может собрать земледелец с участка за один год, если он может засевать разные культуры.
Наибольшее число килограммов урожая летом – это урожай кукурузы, а осенью – урожай риса. Выделим это в таблице:
|
| Рис | Кукуруза | Пшено |
| 1-ый урожай (июнь) | 600 г/м2 | 1200 г/м2 | Не выращивают |
| 2-ой урожай (сентябрь) | 800 г/м2 | Не выращивают | 300 г/м2 |
Складываем эти два числа: 1200+800=2000 г/м2, получаем количество урожая с 1 квадратного метра в граммах. Знаем, что площадь террас равна 360 м2 (мы нашли её в задании номер 3). Значит, надо 2000 умножить на 360, получим: 2000×360=720000 г/м2. Теперь переведем наше число в килограммы, так как это требуется по условию задачи: 720000 г = 720 кг (знаем, что 1 кг=1000 г, поэтому разделили на 1000, убрав три нуля). Наш ответ 720 кг
Ответ: 720
Ответ: см. решение
Задание №1. Найдите объем парного отделения строящейся бани (в куб. м).
Решение
Для решения данного задания надо понимать, что парное отделение бани представляет собой объемную геометрическую фигуру – прямоугольный параллелепипед, а для нахождения объема прямоугольного параллелепипеда надо знать длину, ширину и высоту, затем применяем формулу объема V=abc, где a-длина, b-ширина, c-высота. Эти данные есть в самом начале задачи: длина и ширина по 2,5 м, высота 2,2 м.
Имея эти данные, находим объем: 2,5×2,5×2,2=13,75 куб.м.
Ответ: 13,75
Задание №2. На сколько рублей дровяная печь, подходящая по отапливаемому объему парного отделения, обойдется дешевле электрической с учетом установки?
Решение
Дровяная печь, подходящая по отапливаемому объему парного отделения, это печь «Кентавр», с объемом 13,75 куб.м, а эта величина как раз подходит, так как она удовлетворяет неравенству 10
Нам надо сравнить цены двух печей – «Кентавр» и «Ока» с учетом их установки. По условию задачи для дровяной печи установка не требуется, а для установки электрической печи потребуется подведение специального кабеля, что обойдется в 5000 рублей. Можно разбор решения записать в виде таблицы, где и найдем разницу в цене:
| Печь | Тип | Цена, руб | Установка | Итого | Разница |
| Кентавр | Дровяная | 21000 | 0 руб | 21000 руб | 25000-21000=4000 руб |
| Ока | Электрическая | 20000 | 5000 руб | 25000 руб |
Ответ: 4000
Задание №3. На сколько рублей эксплуатация дровяной печи, которая подходит по отапливаемому объему парного отделения, обойдется дешевле эксплуатации электрической в течение года?
Решение
В данной задаче речь идет об эксплуатации этих же печей, то есть какие затраты в год требуются для каждой из этих печей. А найти надо разницу в стоимости эксплуатации этих печей.
В условии задачи сказано, что за год электрическая печь израсходует 2500 киловатт-часов электроэнергии по 4 руб. за 1 киловатт-час, а дровяная печь за год израсходует 1,8 куб. м дров, которые обойдутся по 1000 руб. за 1 куб. м.
Находим затраты на электропечь: 2500 киловатт-часов электроэнергии по 4 руб. за 1 киловатт-час, это 2500×4=10000 руб.
Находим затраты на дровяную печь: 1,8 куб. м дров по 1000 руб. за 1 куб. м., это 1,81000=1800 руб.
Теперь находим разницу: 10000 – 1800=8200 руб
Ответ: 8200
Задание №4. Доставка печи из магазина до участка стоит 600 рублей. При покупке печи ценой выше 20000 рублей магазин предлагает скидку 5% на товар и 45% на доставку. Сколько будет стоить покупка печи «Кентавр» вместе с доставкой на этих условиях?
Решение
Требуется определить стоимость покупки печи «Кентавр» с доставкой до участка. По условию задачи печь стоит 21000 рублей, а это выше 20000 руб, поэтому положена скидка, как на товар, так и на доставку.
Найдем, сколько будет стоить печь со скидкой 5%: 21000:100×5=1050 руб – скидка на печь 21000 – 1050=19950 руб – стоимость печи со скидкой Найдем, сколько будет стоить доставка со скидкой 45%: 600:100×45=270 руб – скидка на доставку 600 – 270=330 руб – доставка печи со скидкой Найдем, сколько будет стоить печь с доставкой: 19950+330=20280 руб Ответ: 20280
Задание №5. Хозяин выбрал дровяную печь. Чертеж печи показан на рис. 2. Размеры указаны в сантиметрах.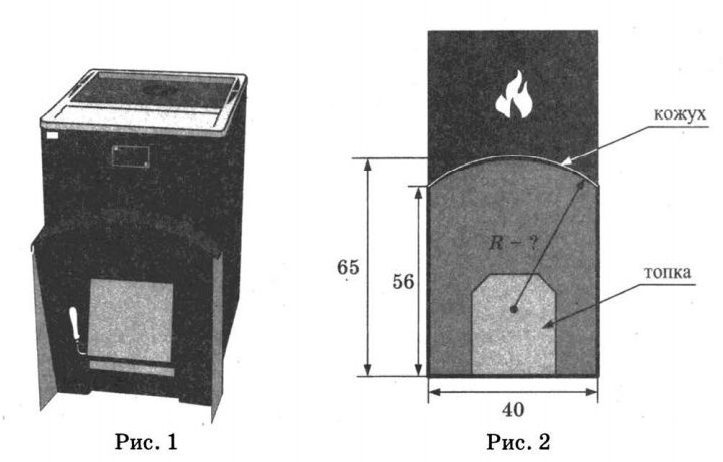
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке по дуге окружности (см. рис.). Для установки печки хозяину понадобилось узнать радиус R закругления арки. Размеры кожуха показаны на рисунке. Найдите радиус в сантиметрах; ответ округлите до десятых.
Решение
На рисунке 2 нам показана именно та часть, с которой мы должны работать на «языке» геометрии. Это показана часть окружности определенного радиуса (он показан стрелкой и буквой R), который мы и должны найти. Если сделать на рисунке свои дополнительные построения, то они будут выглядеть следующим образом (рис.3):
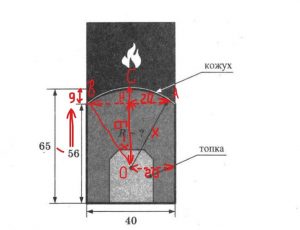
Введем дополнительные обозначения: радиусы пусть будут ОА, ОС, ОВ. Они нам неизвестны. АВ – это хорда, по рисунку видно, что она равна 40. У нас есть равнобедренный треугольник АОВ (АО=АВ=R), ОН – высота по построению.
Рассмотрим треугольник АОН, где угол Н – прямой. Пусть в нем гипотенуза ОА (он же радиус), которая нам неизвестна, будет обозначена х. Видим, что катет АН=20 см, так как АВ=40, а высота ОН, проведенная к основанию АВ, является медианой (свойство равнобедренного треугольника). Найдем катет ОН: слева на рисунке указаны две длины – 65 и 56, а отрезок СН как раз является разницей между ними, т.е. СН=65-56=9. Значит, чтобы найти катет ОН, надо из ОС (а это радиус, который мы обозначили за х) вычесть 9, таким образом, получим, что ОН=х-9.
Итак, в прямоугольном треугольнике имеем: гипотенуза равна х, катеты равны 20 и (х-9). Применим теорему Пифагора (квадрат гипотенузы равен сумме квадратов катетов):
х2=202+ (х-9)2 х2=400 + х2 – 18х + 81 (возвели в квадрат числа и разность двух выражений) 0=481 – 18х (взаимоуничтожили х2 в левой и правой частях уравнения) 18х=481 (перенесли слагаемое с переменной влево, изменяя знак на противоположный) х=481:18 (выполнили нахождение неизвестного множителя действием деления) х=26,7222… (нашли приближенное значение корня уравнения) Значит, радиус, который обозначали за х, будет равен приближенно 26,722… Так как по условию задачи нам надо округлить число до десятых, то по правилу округления, ответ будет 26,7. Ответ: 26,7
Общие советы и рекомендации к данному виду задач
Необходимо помнить простое правило нахождения объема прямоугольного параллелепипеда, а также то, что наши обычные комнаты, бани и парные имеют форму прямоугольного параллелепипеда.
Отличайте покупку печей от их эксплуатации. При покупке оплачивается товар и необходимые к нему дополнительные элементы (например, провод). А эксплуатация – это использование печи, т.е. при этом происходит оплата за свет (если печь электрическая) или за дрова (если печь дровяная).
При решении задания 5 сделайте на своём рисунке дополнительное построение до прямоугольного треугольника, обозначьте радиус (гипотенузу) за х, найдите катеты. При нахождении одного катета просто поделите пополам ширину печки, а при нахождении второго — вычтите из х разницу в длинах, указанных на рисунке слева. Составьте равенство, используя формулировку теоремы Пифагора. Желаем удачи!
Ответ: см. решение
Каждый водитель в Российской Федерации должен быть застрахован по программе обязательного страхования гражданской ответственности (ОСАГО). Стоимость полиса получается умножением базового тарифа на несколько коэффициентов. Коэффициенты зависят от водительского стажа, мощности автомобиля, количества предыдущих страховых выплат и других факторов. Коэффициент бонус-малус (КБМ) зависит от класса водителя. Это коэффициент, понижающий или повышающий стоимость полиса в зависимости от количества ДТП в предыдущий год. Сначала водителю присваивается класс 3. Срок действия полиса, как правило, один год. Каждый последующий год класс водителя рассчитывается в зависимости от числа страховых выплат в течение истекшего года, в соответствии со следующей таблицей:

Задание №1. Павел страховал свою гражданскую ответственность три года. В течение первого года были сделаны две страховые выплаты, после этого выплат не было. Какой класс будет присвоен Павлу на начало четвёртого года страхования?
Решение
По условию задачи имеем, что всегда изначально присваивается водителю 3 класс, поэтому в начале первого года Павлу был присвоен класс 3. Начинаем работать с таблицей. Находим в 1 столбце 3 класс.
В течение первого года были сделаны две страховые выплаты, то есть это значит, что у него было два нарушения ПДД. От класса 3 двигаемся по строке горизонтально до пересечения со столбцом «2 страховые выплаты». Видно, что после двух выплат в течение первого года на начало второго года Павлу был присвоен класс М.

Теперь находим в первом столбце класс М и двигаемся от него горизонтально до пересечения со столбцом «0 страховых выплат», так как в течение второго года у него не было страховых выплат. Получается, что у него на начало 3 года 0 класс.
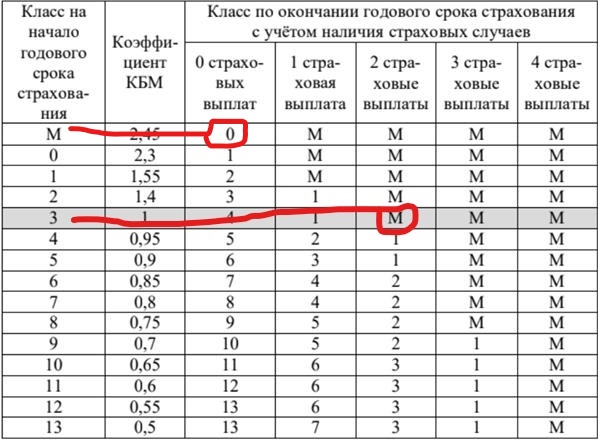
В течение третьего года Павел также не делал страховых выплат, следовательно, находим в таблице в 1 столбце нулевой класс и двигаемся по строке горизонтально до пересечения со столбцом «0 страховых выплат». Получаем, что на начало четвёртого года Павлу будет присвоен класс 1.

Следовательно, ответ в нашем задании – 1 класс.
Ответ: 1
Задание №2. Чему равен КБМ на начало четвёртого года страхования?
Решение
Начнем с того, что такое КБМ. Об этом сказано в условии задачи: КБМ – коэффициент бонус-малус, который зависит от класса водителя. Это коэффициент, понижающий или повышающий стоимость полиса в зависимости от количества ДТП в предыдущий год.
По условию мы знаем, что в начале первого года Павлу был присвоен класс 3. А по решению 1 задачи имеем: после двух выплат в течение первого года на начало второго года Павлу был присвоен класс М. Поскольку в течение второго года Павел не делал страховых выплат, на начало третьего года Павлу был присвоен класс 0. В течение третьего года Павел также не делал страховых выплат, следовательно, на начало четвёртого года Павлу будет присвоен класс 1. Работаем с таблицей, находим 1 класс в первом столбце и идем до пересечения со столбцом «КБМ»: КБМ на начало четвёртого года страхования равен 1,55.

Ответ: 1,55
Задача №3. Коэффициент возраста и водительского стажа (КВС) также влияет на стоимость полиса (см. таблицу)

Когда Павел получил водительские права и впервые оформил полис, ему было 24 года. Чему равен КВС на начало 4-го года страхования?
Решение
Когда Павел впервые получил права и оформил полис, ему было 24 года, значит, на начало второго года ему было 25, на начало третьего – 26, а на начало 4-ого – 27 лет. Следовательно, на начало 4 года страхования он будет попадать в возрастную категорию 25−29 лет (смотрим таблицу), а его стаж будет попадать в промежуток 3−4 года. Совмещаем по таблице эти две категории и на пересечении находим, что КВС равен 1,04.

Ответ: 1,04
Задача №4. В начале третьего года страхования Павел заплатил за полис 18745 руб. Во сколько рублей обойдётся Павлу полис на четвёртый год, если значения других коэффициентов (кроме КБМ и КВС) не изменятся?
Решение
По условию задачи сказано, что стоимость полиса получается умножением базового тарифа на несколько коэффициентов – КБМ и КВС.
Зная, что в начале третьего года страхования Павел заплатил за полис 18745 руб, а значение базового тарифа не меняется, мы можем рассчитать стоимость страховки. Для этого нужно знать базовый тариф.
Итак, сначала найдём КБМ и КВС на начало третьего года.
По решению задачи 2 у нас известно, что на начало 3-го года Павел имел 0 класс, следовательно, по таблице — КБМ будет равен 2,3.
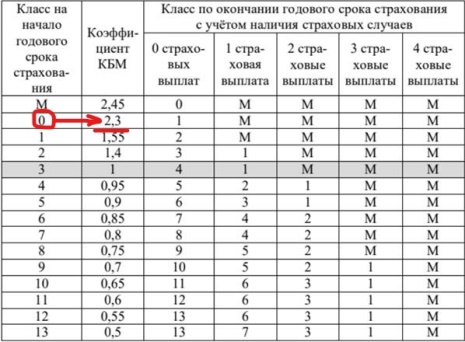
Дальше надо найти КВС: так как мы ищем его на начало 3-его года, то стаж водителя был 2 года, а возраст 26 лет (смотрим задачу 3), он попадает в категорию 25-29. Итак, работаем с таблицей и находим, что КВС на начало третьего года равен 1,63.

Теперь, зная, что страховка была 18745 руб, КБМ равен 2,3, а КВС равен 1,63, составим равенство: 18745=х•2,3•1,63, где х – это базовый тариф.
Находим х, как неизвестный множитель, разделив 18745 на произведение 2,3•1,63, т.е.
Х=18745: (2,3•1,63)=5000 рублей
Теперь можно находить стоимость страховки на 4-й год.
Итак, базовый тариф равен 5000 руб, КБМ на начало четвёртого года равен 1,55 (задача 2), КВС на начало четвёртого года равен 1,04 (задача 3). Значит, на начало четвёртого года стоимость полиса равна: 5000∙1,55∙1,04=8060 рублей
Ответ: 8060 рублей
Задача №5. Павел въехал на участок дороги протяжённостью 2,7 км с камерами, отслеживающими среднюю скорость движения. Ограничение скорости на дороге — 60 км/ч. В начале и в конце участка установлены камеры, фиксирующие номер автомобиля и время проезда. По этим данным компьютер вычисляет среднюю скорость на участке. Павел въехал на участок в 11:03:16, а покинул его в 11:05:31. Нарушил ли Павел скоростной режим? Если да, на сколько км/ч средняя скорость на данном участке была выше разрешённой?
Решение
Чтобы определить, были ли нарушения ПДД на данном участке пути, нужно знать, с какой скоростью он его проехал. Для нахождения скорости нам нужно знать время и расстояние.
По условию задачи мы знаем, что расстояние равно 2,7 км. Вычислим время: так как на участок Павел въехал в 11:03:16, а покинул его в 11:05:31, то вычтем из11:05:31 число11:03:16, получим 2:15, то есть 2 минуты 15 секунд – это 135 секунд. Нам надо перевести их в часы: в 1 часе 3600 секунд, значит, 1353600=380.
Найдем теперь скорость, нужно разделить расстояние 2,7 км на время, т.е. на 380 часа. Итак, 2,7:380=2710×803=72 км/ч. Видно, что на участке с разрешенной скоростью 60 км/ч Павел ехал со скоростью 72 км/ч. Он нарушил скоростной режим, превысив её на 12 км/ч.
Ответ: 12
Ответ: см. решение