Управление образования администрации города Черемхово
Муниципальное общеобразовательное учреждение
« Лицей г. Черемхово »
Муниципальная научно-практическая конференция юниоров и старшеклассников «В мир поиска, в мир творчества, в мир науки»
Таинственная красота и закономерность числовых отношений
Вид работы: исследовательская
Автор: учащаяся 8 класса
Петрова Наталья
Руководитель: Юрчишина Наталья Александровна,
учитель математики
г. Черемхово
2016
Содержание
| Введение | 3 |
| Обзор литературы | 4 |
| 1. Числа Фибоначчи: секрет мироздания | 6 |
История чисел Фибоначчи | 6 |
Ряд Фибоначчи | 7 |
Золотое сечение | 9 |
| 2. Решение задач, связанных с числами Фибоначчи и Золотым сечением | 13 |
| 2.1.Решение задач с числами Фибоначчи | 13 |
| 2.2 Задачи на Золотое сечение | 15 |
| Заключение | 17 |
| Список использованных источников | 18 |
| Приложение |
|
ВВЕДЕНИЕ
Числа управляют миром! Число – это
сила, царящая над богами и смертными!-
Древние пифагорейцы
Известно, что математику называют «царицей всех наук». Пока математика остается для человека набором скучных задачек в учебнике, вряд ли он может прочувствовать красоту, универсальность и даже юмор этой науки. Но встречаются в математике темы, которые делают любопытнее наблюдения за обычными для нас вещами и явлениями, вызывая желание попытаться проникнуть за завесу тайны создания Вселенной. Все необычные закономерности мироздания могут быть описаны с помощью математики, подчинены определенным числовым соотношениям.
Проблема заключается в необходимости ответа на вопрос: почему же последовательность чисел Фибоначчи столь распространена в нашем мире?
Актуальность выбранной темы заключается в том, что она является дополнением и углублением математических и исторических знаний, прививает любовь к прекрасному.
Цель исследовательской работы: исследование закономерностей числового ряда Фибоначчи и Золотого сечения, их проявления в строении живых и неживых объектов.
Для достижения поставленной цели необходимо решить следующие
задачи исследования:
Изучить числа Фибоначчи, способы построения ряда Фибоначчи и Золотого сечения;
Рассмотреть примеры золотого сечения в живой и неживой природе;
Изучить и применить способы решения задач, связанных с числами Фибоначчи, при нахождении Золотого сечения в окружающем мире.
Объект исследования: задачи, связанные с числами Фибоначчи и
Золотым сечением.
Предмет исследования: способы решения задач, связанных с числами Фибоначчи, при нахождении примеров Золотого сечения в окружающем мире.
Практическая значимость: использование приобретенных знаний и навыков исследовательской работы при изучении школьных предметов.
Методы исследования:
Теоретический (логическая ступень познания).
Эмпирический (наблюдение, эксперимент, измерение).
Практический (расчеты числа фи)
Гипотеза основывается на предположении, что если в окружающем нас мире всё построено по удивительно гармоничным законам с математической точностью, значит, всё в мире продуманно и просчитано самым главным нашим дизайнером – Природой!
Обзор литературы
Мы обратились ко многим источникам информации и прочитали о числах Фибоначчи, о Золотом сечении, которые таят в себе великую загадку мира.
В книге Марио Ливио «φ – число Бога. Золотое сечение – формула мироздания» представлены основные понятия о загадочном числе φ, приведены малоизвестные факты из истории, рассматривается математическая теория Золотого сечения.1
В журнале «Молодой ученый» № 21, 2014 г. в статье Первушкиной Е. А.,
Калининой А. И. «Решение геометрических задач методом «Золотого сечения» представлены основные способы решения задач на Золотое сечение основных геометрических фигур.
В Приволжском научном вестнике» № 8-2, 2014, представлена статья Напалкова С.В., Первушкиной Е.А. «WEB-КВЕСТ как средство развития инновационной стратегии образования», в которой говорится о примерах золотого сечения в окружающем мире.
2 На сайтах http://n-t.ru/tp/iz/zs и http://www.problems.ru/view_search_new.php представлен теоретический материал о биографии Леонардо Пизанского, об истории чисел Фибоначчи, о принципах формообразования в природе и т.д., приводятся олимпиадные задачи, связанные с числами Фибоначчи.
В школьном курсе математики данная тема не раскрывается полностью. Это указывает на недостаточно высокую степень изученности Золотого сечения в образовательной деятельности, свидетельствует об актуальности и большой практической значимости исследовательской работы «Таинственная красота и закономерность числовых отношений».
Числа Фибоначчи: ищем секрет мироздания
История чисел Фибоначчи
Изучение последовательности чисел Фибоначчи и Золотого сечения привлекает учёных с древности и до наших дней. Еще до нашей эры понятие о Золотом делении ввел в научный обиход древнегреческий философ и математик Пифагор.
Леонардо Пизанский, сын торговца, впоследствии стал математиком и получил признание потомков в качестве первого крупного математика Европы. Путешествую вместе с отцом на Восток, Леонардо изучал математику у арабских учителей, которые в те времена были в этом деле, да и во многих других науках, одними из лучших специалистов. С трудами математиков Античности и Древней Индии он познакомился в арабских переводах и, осмыслив все прочитанное, Фибоначчи написал несколько научных трактатов по математике, включая «Книгу абака». Кроме нее им были созданы:
«Practica geometriae» («Практика геометрии», 1220 год);
«Flos» («Цветок», 1225 год – исследование, посвященное кубическим уравнениям);
«Liber quadratorum» («Книга квадратов», 1225 год – задачи о неопределенных квадратных уравнениях).
Биографических сведений о жизни Леонардо осталось очень мало. Что же касается имени Фибоначчи, то оно закрепилось за ним только в XIX веке. Слово Fibonacci - сокращение от двух слов «filius Bonacci», появившихся на обложке «Книги абака».3
Наблюдая за различными явлениями и живой природой, Фибоначчи открыл самую невероятную в мире последовательность чисел. Соотношение между всеми числами в такой последовательности равно золотому сечению, Золотая пропорция сыграла не маловажную роль в его достижениях. В начале XIII века данную последовательность Фибоначчи описал в своем труде «Liber abaci» («Книга абака», 1202 г.). Золотое сечение считают одним из важнейших принципов Природы, формирующем под влиянием гармонии представление о «красивом».
Древнеиндийские математики стали пользоваться «числами Фибонач-чи» раньше, чем в Европе. Сам Фибоначчи при жизни никогда не называл себя Фибоначчи – это имя стали применять к Леонардо Пизанскому только спустя несколько столетий после его смерти.
1.2. Числа Фибоначчи
Числами Фибоначчи называют элементы числовой последовательности, в которой каждое следующее число в ряду получается суммированием двух предыдущих чисел.
Рассмотрим последовательность: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987…
Данную последовательность можно представить в виде формулы:
F0 = 0, F1 = 1, Fn = Fn-1 + Fn-2, n ≥ 2
Если ряд чисел Фибоначчи будет начинаться с отрицательных значений n, то последовательность станет двусторонней (т.е. охватит и отрицательные, и положительные числа) и в обоих направлениях будет стремится к бесконечности.
Пример такой последовательности: -55, -34, -21, -13, -8, 5, 3, 2, -1, 1, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. В этом случае формула выглядит так:
Fn = Fn+1 - Fn+2 ,
а может быть преобразована: F-n = (-1)n+1Fn.
Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (напpимеp, 13:8), результатом будет величина, колеблющаяся около иppационального значения 1,61803398875... и через pаз то превосходящая, то не достигающая его. Узнать соотношение точно невозможно, и потому в алгебре общепринято его обозначение греческой буквой φ (фи) φ=1,618.
При нахождении отношения других чисел из последовательности Фибоначчи, не ближайших, а, например, через одно или через два числа
получим: для членов последовательности, взятых через один получим число, стремящееся к 2,618. При вычислении отношения старшего члена к младшему через два числа последовательности, результат будет стремиться к 4,236. Если рассмотреть по такому же принципу найти отношения младших членов последовательности к старшим (через один или через два члена), то будут получены практически обратные значения уже полученным числам: 0,382 (обратное значение числа 2,618), следующее – 0,236 (обратное значение 4,236) и так далее. На первый взгляд, это всё просто любопытные сведения, игра цифр, не имеющая практической реализации. Однако это совсем не так.
Последовательность Фибоначчи асимптотически ( приближаясь все
медленнее и медленнее) стpемится к некотоpому постоянному соотношению. Однако, это соотношение иppационально, то есть пpедставляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифp в дpобной части.
Особый интерес представляет задача о кролика, в результате решения которой Леонардо получил ряд чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 и т.д.
Эта задача о кроликах гласила:
«Некто поместил пару кроликов в некотором месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а потомство кролики приносят со второго месяца своего рождения. Сколько пар кроликов в один год от одной пары рождается?» 4
Решая эту задачу, получаются следующие результат: в начале 1 месяца была 1 пара, в начале 2 месяца – 2 пары (зрелая и молодая), в начале 3 месяца – 3 пары (две зрелые и одна молодая) и так далее (рис. 1).
Для решения составим таблицу:
| № п\п |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Кол-во пар зрелых кроликов | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 |
| Кол-во всех пар | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 |
Таблица 1. Задача о кроликах
Общее число пар кроликов, рождённых от одной пары за год, равно 377. При решении этой задачи найти число всех пар кроликов в каком-либо месяце. Для этого нужно сложить число всех пар кроликов, которые уже были
в прошлом месяце с числом зрелых пар кроликов прошлого месяца, которые теперь дадут потомство. Учитывая, что число зрелых пар прошлого месяца равно числу всех пар позапрошлого месяца, получаем закономерность: число всех пар кроликов данного месяца равно сумме чисел всех пар кроликов за два предыдущих месяца и т.д. Подсчёт можно делать по порядку до бесконечного числа месяцев.
Связь с жизнью
Кролики отличаются своей плодовитостью. Не будь смерти, потомство одной пары довольно быстро заполнило бы всю Землю. Например, в 1859 году в Австралию из Англии было привезено 24 кролика, которых там никогда не было. В отсутствии хищников, кролики расплодились быстрыми темпами, их полчища наводнили Австралию, стали бедствием для австралийцев, так как уничтожали многочисленные посевы. На борьбу с ними были затрачены огромные средства. Кролики остаются в Австралии проблемой и поныне.
Золотое сечение
Очень любопытно одно из свойств последовательности чисел Фибоначчи. Если взять две последовательные пары из ряда и разделить большее число на меньшее, результат будет постепенно приближаться к золотому сечению.
Чтобы познакомиться с понятием «Золотое сечение» ближе, рассмотрим два практических задания.
Первое практическое задание «Рука человека»
Если приблизить ладонь к себе, внимательно посмотреть на указательный палец, и сразу можно увидеть в нем формулу золотого сечения. Каждый палец состоит из трех фаланг. Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число Золотого сечения (за исключением большого пальца).
Второе практическое задание « Скамья»
«Вы подходите к пустой скамейке и садитесь на нее. Где вы сядете — посередине или самого края?» Скорее всего, не то и не другое. Вы сядете так, что отношение одной части скамейки к другой, относительно вашего тела, будет равно примерно 1,62, причем абсолютно инстинктивная. Садясь на скамейку, человек производит «золотое сечение».
«Золотое сечение - деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине».
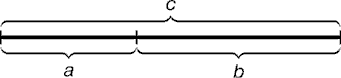
a : b = b : c или с : b = b : а
Рис. 1 – Золотое сечение
Как оказалось, пропорции золотого сечения можно обнаружить во всем - в произведениях искусства, в природе, в архитектуре (Нотр Дам де Пари, великие египетские пирамиды), в музыке (произведения Моцарта), в алфавите некоторых народов, даже биржевые курсы наделены данным свойством.
В своей статье «Модель развития геометрической креативности школьников при обучении математике в 5-6 классах с использованием информационных технологий» Первушина Е.А. пишет: « В живой природе «золотое сечение» встречается в некоторых видах морских звезд, раковинах моллюсков, рогах млекопитающих; в химии сечение встречается в белковых
цепях нуклеиновых кислот; в медицине этот термин связывают с работой
сердца и его мышечной системой; в архитектуре сечение представлено в различных проектах домов, в здании Кремля; в математике и геометрии «золотое сечение» образует геометрическую фигуру – икосаэдр, грани которого представлены 20 равносторонними треугольниками; также данный метод применятся для решения геометрических задач».5
Чаще всего золотое сечение встречается в природе: тело и лицо человека, ритм сердца, даже почерк. Например, при проведении исследования частей тела человека получили, что пупок расположен на уровне 0,618 от его роста, а это и есть уже известное нам число φ = 1,618. (приложение 1).
Исследовав научно-популярные источники. Можно сделать вывод, что Человек – просто кладезь числа фи. У него одно туловище, одна голова, одно сердце. Многие части тела парные, например, руки, ноги, глаза, почки. Ноги, руки, пальцы рук состоят из трех частей. На руках и ногах по пять пальцев, а рука вместе с пальцами состоит из восьми частей. В данный момент у человека насчитывается 12 пар рёбер, но в прошлом было 13 пар рёбер, в процессе эволюции количество рёбер уменьшилось. Позвоночник состоит из 34 позвонков.
Характерными особенностями обладает и кисть человека. Она состоит из трех основных частей: запястья, пясти и пальцев. Каждый палец состоит из трех фаланг.
У ребёнка число молочных зубов равно 20, а у взрослого - 32, причём последняя пара («зубы мудрости») появляется позже других и не у всех людей.
Дискретность «по Фибоначчи» прослеживается и довольно отчетливо и не только на костях скелета. Даже волос человека не является простым образованием. Он образует систему, в которую входит сосочек, луковица, корень, пучок мышц, сальная железа, нерв, кровеносные сосуды и стержень – всего восемь частей, маленьких самостоятельных органов, обеспечивающих жизнедеятельность волоса.
В состав крови входят красные кровяные тела (эритроциты), белые кровяные тела (лейкоциты) и тромбоциты. Эти три типа кровяных тел содержатся в пропорции 62 32 6. Отношение эритроцитов к двум остальным телам крови отвечает золотой пропорции.
Линейные узоры на концах пальцев неповторимы для каждого человека. Выделено три основных типа: петлевые, круговые и дуговые.
Из приведенного перечисления видно, что в членении тела человека на части присутствуют числа Фибоначчи от 1 до 34. Общее число костей скелета человека близко к 233, то есть соответствует еще одному числу Фибоначчи. На этом список не заканчивается. Случайно ли это? Скорее всего - нет. Человек,
как и другие творения природы, подчиняется всеобщим законам развития.
Еще одну параллель между числами Фибоначчи и золотым сечением позволяет провести «золотой прямоугольник» или прямоугольник с пропорциями золотого сечения: его стороны соотносятся в пропорции 1,618 к 1. Например, построим прямоугольник, а длины сторон зададим равными двум последовательным члена ряда Фибоначчи а = 8, b = 13. Выполним его деление
на 2 прямоугольника больший и меньший так, что длины их сторон вновь соответствовали числам Фибоначчи, т.е. длина стороны большего прямоугольника должна быть равной сумме сторон двух меньших прямоугольников (рис. 1).
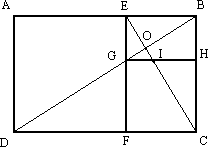
Рис. 1 Отношение сторон Золотого прямоугольника
Золотой прямоугольник обладает и другими необычными свойствами. Например, если отрезать от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, получим золотой прямоугольник, но уже меньших размеров. Продолжив этот процесс, мы будем получать все меньшие и меньшие золотые прямоугольники. Располагаться они будут по логарифмической спирали, которая играет важную роль в математических моделях природных объектов. В природе ярким примером являются улитки.
Спираль Фибоначчи мы можем увидеть в самых неожиданных предметах и явлениях. Например, расположение семечек подсолнуха, ячеек и шишек ананаса, спиралью закручивается ураган, облака циклона. В форме спирали Фибоначчи пауки плетут свою сеть, а стадо разбегается от хищника.
Современная наука считает, что Вселенная развивается по золотой
спирали. Эта спираль не имеет конца и начала. Ее меньшие витки никогда не
сходятся в одну и ту же точку, а большие - развиваются в пространстве.
Спирали есть и в человеке. С помощью нее мы слышим. Спирали есть на наших ладонях и пальцах.
В животном и растительном мире мы также можем найти множество примеров спиралей. В форме спирали развиваются рога и бивни животных,
когти львов и клювы попугаев.
Вывод: В нашей жизни числовой ряд Фибоначчи и Золотое сечение широко представлены: в строении живых существ, сооружений, с его помощью даже описывается устройство Галактики.
2. Решение задач, связанных с числами Фибоначчи и Золотым сечением
Изучив литературу, рассмотрев сайты математической тематики, мы выявили, что задачи, связанные с числами Фибоначчи встречаются очень часто. Для их решения и требуется применять индивидуальный способ решения.
Рассмотрим решение задач такого вида.
2.1. Решение задач с числами Фибоначчи
Задача 2.1.1.
«О том, как прыгают кузнечики» Предположим, что имеется лента, разбитая на клетки и уходящая вправо до бесконечности. На первой клетке этой ленты сидит кузнечик. Из любой клетки кузнечик может перепрыгнуть либо на одну, либо на две клетки вправо. Сколькими способами кузнечик может добраться до n-ой от начала ленты клетки? 6
Решение:
Пусть an — количество способов, которыми кузнечик может добраться до n-ой клетки. Тогда a1 = a2 = 1. Кроме того, в n + 1-ую клетку кузнечик может попасть либо из n-ой клетки, либо перепрыгнув n-ую клетку. Поэтому an + 1 = an - 1 + an. Отсюда an = Fn - 1.
Ответ: an = Fn - 1.
Задача 2.1.2.
Петя поднимается по лестнице из 10 ступенек. За один раз он прыгает вверх либо на одну ступеньку, либо на две ступеньки. Сколькими способами
Петя может подняться по лестнице?
Решение:
Обозначим через аn число способов подняться на лестницу из n ступенек, соблюдая условия задачи. Очевидно, a1 = 1, a2 = 2.
Пусть Петя запрыгивает на лестницу из n 2 ступенек. Если первый прыжок был на две ступеньки, то ему осталось запрыгнуть на n – 2 ступеньки, и число способов закончить подъем равно an–2. Если же первый прыжок был на одну ступеньку, то число способов закончить подъем равно an–1. Значит, an = an–1 + an–2.
Это равенство позволяет, зная a1 и a2, вычислять последовательно все an (при этом будут получаться известные числа Фибоначчи):
a3 = 3, a4 = 5, a5 = 8, a6 = 13, a7 = 21, a8 = 34, a9 = 55, a10 = 89.
Ответ: 89 способов.
Задача 2.1.3.
Дана последовательность чисел 1, 2, 3, 5, 8, 13, 21, ..., в которой каждое число, начиная с третьего, равно сумме двух предыдущих. В этой последовательности выбрано восемь чисел подряд. Докажите, что их сумма не
равна никакому числу рассматриваемой последовательности.
Решение:
Пусть S = ak+1 + ak+2 + ... + ak+8 – сумма восьми идущих подряд членов последовательности.
Достаточно доказать, что ak+9 S k+10.
Левое неравенство очевидно: S ak+7 + ak+8 = ak+9.
Докажем правое неравенство.
Ясно, что ak+10 = ak+8 + ak+9 = ak+8 + ak+7 + ak+8 = ak+6 + ak+7 + ak+7 + ak+8 = ak+5 + ak+6 + ak+6 + ak+7 + ak+8 = ak+1 + 2ak+2 + ak+ 3 + ... + ak+8. Последнее выражение, очевидно, больше S. Что требовалось доказать.
Задача 2.1.4.
Чему равны числа Фибоначчи с отрицательными номерами F-1, F-2, ..., F-n,...?
Решение:
Из начальных условий F0 = 0, F1 = 1 и рекуррентного соотношения Fn + 2 = Fn + 1 + Fn числа Фибоначчи с отрицательными номерами определяются однозначно: F-n = (- 1)n + 1Fn.
Ответ: F-n = (- 1)n + 1Fn.
2.2. Задач на Золотое сечение
Задача 2.2.1.
Построить золотое сечение отрезка ВС.
Решение:
Построить золотое сечение отрезка ВС, значит найти точку К такую, что = . Рассмотрим прямоугольный треугольник DBC, у которого один катет в 2 раза больше другого. Проведем из точки С перпендикуляр к прямой ВС и на нем отложим отрезок СD, длина которого равна половине стороны ВС. СD=BC. Затем, соединим точки В и D. Отложим отрезки DE и ВК так, что длина отрезка DE равна длине отрезка DC, а отрезок BK = АN. Точка K является искомой, она производит золотое деление отрезка BC.
Задача 2.2.2.
Вырежьте из бумаги прямоугольник со сторонами 10 см и 16 см.
Отрежьте от него квадрат наибольшей площади. Измерьте стороны получившегося прямоугольника.
Решение:
1.Построение золотого прямоугольника
а) Рассмотрим прямоугольник АВСД: Пусть стороны АВ=16 см, ВС=10 см. Тогда отношение сторон примет следующий вид: АВ:ВС=16:10=1,6.
б) Рассмотрим прямоугольник КВСМ: так как ВС=КМ=10 см, а КВ=АВ-АК=16-10=6 см. Получим следующее отношение сторон КМ:КВ = 10 : 6= 1,6666…см. в) Рассмотрим прямоугольник МPNC: так как СN=ВС-ВN=10-6=4 см, а МС=ДС-ДМ=16-10=6 см, то отношение сторон МС:СN примет следующий вид МС : СN = 6 : 4 = 1,5 см. Получили золотой прямоугольник.
Рассмотрено решение алгебраических и геометрических задач с помощью числового ряда Фибоначчи и метода «золотого сечения». Использование предложенных видов заданий позволяет развивать творческие способности, исследовательские навыки и активизировать познавательную деятельность, существенным образом интенсифицировать процесс обучения математике.
Заключение
Загадка чисел Фибоначчи –
Преемственность большой игры.
Мы друг для друга что-то значим,
Пока рождаются миры.
В результате проделанной мною работы была изучена последовательность и свойства чисел Фибоначчи, которая заключается в том, что сумма двух соседних чисел последовательности дает значение следующего за ними. Я изучила и проанализировала проявление чисел последовательности Фибоначчи в окружающей нас действительности.
Числовой ряд Фибоначчи и Золотое сечение широко представлены в нашей жизни: в строении живых существ, в неживой природе, с его помощью даже описывается устройство Галактик. Все это свидетельствует об универсальности математической загадки числового ряда Фибоначчи. Также я увидела строгую математику в строении человека. Узнала об особенностях природы спирали Фибоначчи.
При решении задач я на практике увидела значимость чисел Фибоначчи в процессе изучения математики.
Таким образом, сформулированные цель и задачи исследования достигнуты, а его гипотеза нашла своё подтверждение. Моя гипотеза о существовании особых числовых закономерностей, которые отвечают за гармонию, подтвердилась. Действительно, всё в мире продуманно и просчитано самым главным нашим дизайнером – Природой! И математика – это очень важный инструмент для познания тайн чисел
Список использованных источников
Марио Ливио. φ – число Бога. Золотое сечение – формула мироздания. - М. - АСТ, 2015, с. 432.
Напалков С.В., Первушкина Е.А. WEB-КВЕСТ как средство развития инновационной стратегии образования // Приволжский научный вестник. – 2014. – № 8-2 (36).– с. 51-53.
Первушкина Е.А., Калинина А.И. Решение геометрических задач методом «Золотого сечения»//Молодой ученый, № 21, 2014, с.207-210.
Первушкина Е.А., Модель развития геометрической креативности школьников при обучении математике в 5-6 классах с использованием информационных технологий // Школа будущего. – 2011. – № 6. – с. 58-64.
http://www.problems.ru/view_search_new.php
http://n-t.ru/tp/iz/zs
1� Марио Ливио.Число Бога. Золотое сечение – формула мироздания.- М.- АСТ, 2015. – С. 13.
2� Напалков С.В. и др. WEB-KBECT как средство развития инновационной стратегии образования// Приволжский научный вестник, № 8-2. – 2014. – С.51.
3� http://n-t.ru/tp/iz/zs
4� http://www.problems.ru/view_search_new.php
5� Первушкина Е.А. Решение геометрических задач методом «Золотого сечения»//Молодой ученый, № 21- 2014.-С. 207
6� http://www.problems.ru/view_search_new.php



















