
Муниципальное общеобразовательное учреждение
средняя общеобразовательная школа «Созвездие»
муниципального образования городской округ Люберцы Московской области
140015, Московская область, город Люберцы, Телефон 8 (903) 264-82-78
Солнечная ул, дом 1 E-mail: lbrc_sozvezdie@mosreg.ru
МАТЕМАТИКА
Итоговая работа по математике,
критерии оценивания ответа
5 класс
базовый уровень
Разработчик:
Л.В. Чернова
учитель математики
г. о. Люберцы
2025
Итоговая работа составлена в соответствии с действующей программой по математике на основе Федерального государственного образовательного стандарта основного общего образования и предназначена для проведения промежуточной аттестации по математике в 5 классе, с базовым изучением предмета.
Цель: установление фактического уровня теоретических знаний, обучающихся по математике обязательного компонента учебного плана, их практических умений и навыков; установление соответствия уровня ЗУН обучающихся требованиям Федерального государственного образовательного стандарта основного общего образования.
Задачи: проверка уровня предметной компетентности учащихся 5 класса по математике за курс 5 класса в рамках проведения промежуточной аттестации.
Время проведения 60 минут.
Форма работы: письменно, по контрольно-измерительным материалам.
Количество вариантов – 2.
Характеристика структуры и содержания работы
Каждый вариант работы содержит 3 части.
1 часть содержит 10 заданий базового уровня сложности, 2 часть содержит 2 задания повышенного уровня сложности, 3 часть содержит 1 задание высокого уровня. Основное назначение 2 и 3 части – дифференцировать хорошо успевающих школьников по уровням подготовки.
Обучающиеся должны продемонстрировать умения выполнять арифметические действия с обыкновенными и десятичными дробями, с числами с разными знаками, решать уравнения, раскрывать скобки и приводить подобные слагаемые, находить неизвестный член пропорции, находить целое по его части, решать задачи на движение, отмечать точки на координатной плоскости.
Оценка выполнения отдельных заданий и работы в целом.
Все задания 1 части оцениваются в 1 балл; каждое задание 2 части оценивается в 3 балла. Во всех заданиях требуется записать решение и ответ. Ответ без решения оценивается в 0 (нуль) баллов. В 3 части оценивается в 2 балла, нужно записать ход решения и ответ. Ответ без решения оценивается в 0 (нуль) баллов.
Выполнение учащимися работы в целом определяется суммарным баллом, полученным им по результатам выполнения всех заданий работы. Максимальный балл работы – 19 баллов.
Критерии оценивания результатов выполнения работы.
Рекомендации по переводу первичных баллов в отметки по пятибалльной шкале
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Первичные баллы | 0-8 | 9-13 | 14-18 | 19-25 |
Указания к оцениванию задания №11
| Выбран правильный ход решения, получен верный ответ | 5 баллов |
| За каждое верное выполнение вычислительных действий | 1 балл |
| Выбран неверный ход решения, вычисления в действиях выполнены без ошибок | 1 балл |
| Другие случаи | 0 баллов |
| Максимальный балл | 5 баллов |
Указания к оцениванию задания №12
| Указан правильный порядок действия, получен верный ответ | 5 баллов |
| Каждое верно выполненное действие | 1 балл |
| Другие случаи | 0 баллов |
| Максимальный балл | 5 баллов |
Указания к оцениванию задания №13
| Выбран правильный ход решения, получен верный ответ | 5 баллов |
| При верном ходе решения задачи допущена одна вычислительная ошибка, с ее учетом решение доведено до конца | 1 балл |
| Выбран неверный ход решения, вычисления в действиях выполнены без ошибок
| 1 балл |
| Верно переведены обыкновенные дроби в десятичные, за каждую дробь по 1 баллу | 2 балла |
| Верное округление числа | 1 балл |
| Другие случаи | 0 баллов |
| Максимальный балл | 5 баллов |
5 класс
Итоговая работа для промежуточной аттестации по математике
Демонстрационный вариант
Группа А
(Каждый правильный ответ – 1 балл)
1. Запишите в виде десятичной дроби число сто одна целая сто одна десятитысячная.
Ответ: а) 101,101; б) 101,0101; в) 1010,01; г) 101,00101.
2. Представьте в виде неправильной дроби смешанное число 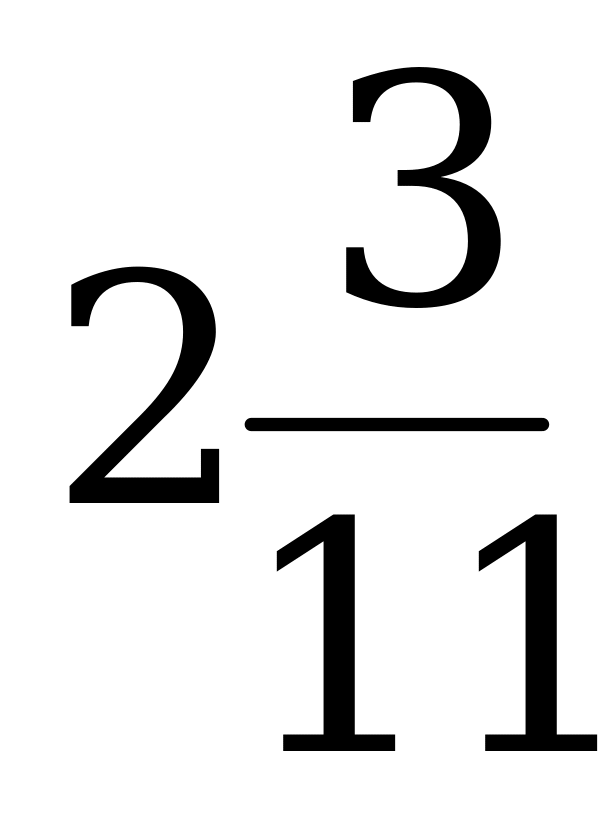 .
.
Ответ: а) �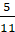 � б) �
� б) � � в) �
� в) �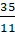 � г) �
� г) �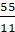 �.
�.
3. Выполните сложение: 4,1 + 2,51.
Ответ: а) 2,92; б) 6,52; в) 6,61; г) 4,351.
4. Выполните вычитание: 13,1 – 2,51.
Ответ: а) 10,6; б) 10,51; в) 11,5; г) 10,59.
5. Выполните вычитание: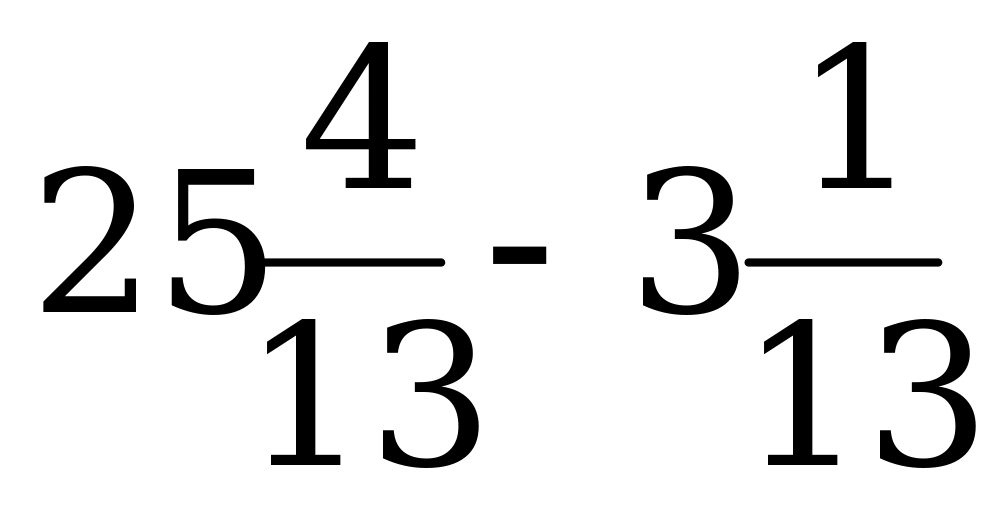
Ответ: а) �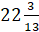 � б) �
� б) �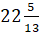 � в) �
� в) �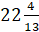 � г) �
� г) �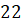 �
�
6. Найдите сумму дробей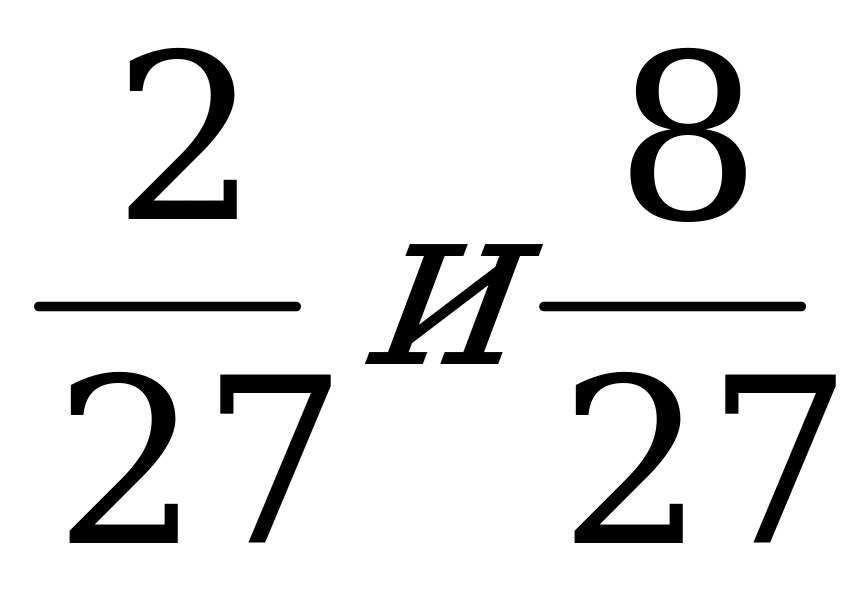 ?
?
Ответ: а) �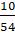 � б) �
� б) �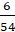 � в) �
� в) �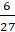 � г) �
� г) �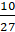 �
�
7. Выполните деление: 0,51 : 1,7
Ответ: а) 0,03; б) 3; в) 0,3; г) 0,35.
8. Выполните умножение: 1,03 ∙ 5,4
Ответ: а) 5,562; б) 55,62; в) 556,2 г) 1,512.
9. Найдите среднее арифметическое чисел 23 и 37.
Ответ: а) 25; б) 26; в) 30 г) 60.
10. Найдите корень уравнения: 45 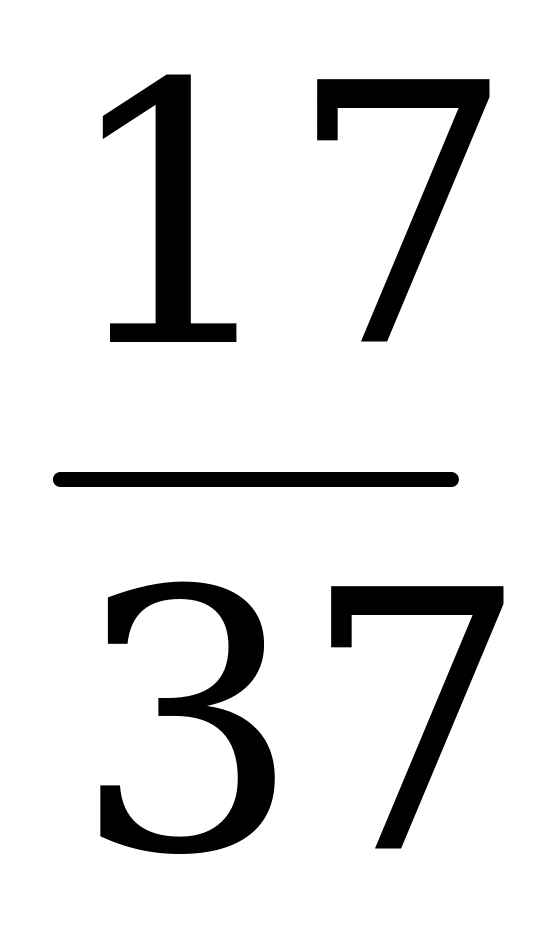 – х = 31
– х = 31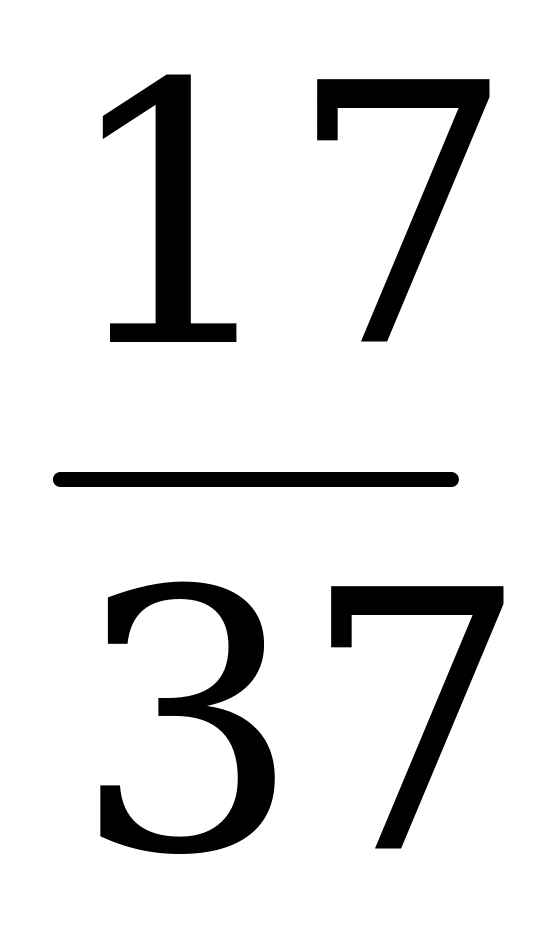
Ответ: а) 45 б) 31 в) 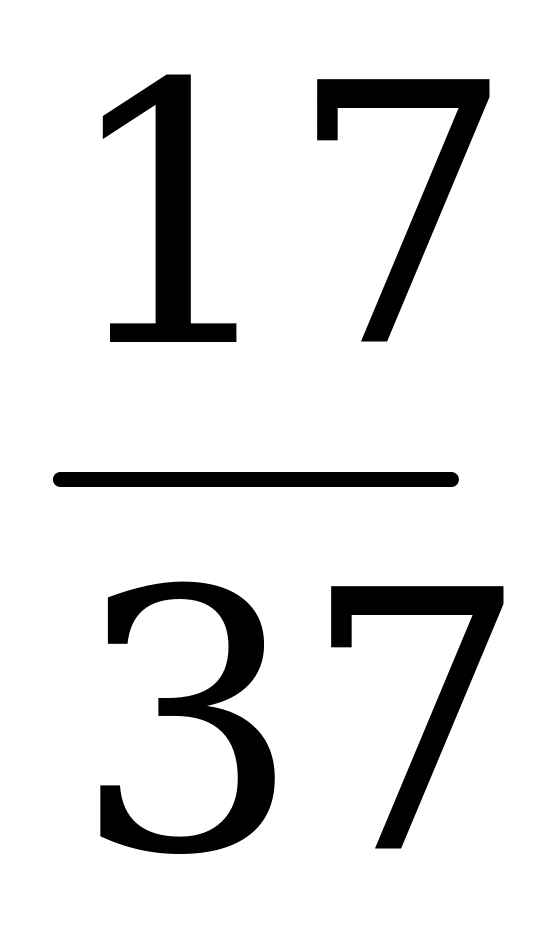 г) 14
г) 14
Группа Б
(Каждое правильное и полное решение – 5 баллов)
11. Турист шел первые 2 часа пути со скоростью 5,4 км/ч, а затем 3 часа со скоростью 4,8 км/ч. Какова его средняя скорость?

12. Вычислите: ( 37,41 : 4,3 + 1,3 ∙ 2,6 ) : 0,4.

Группа В
(Каждое правильное и полное решение – 5 баллов)
13. Решите уравнение: ( 0, 006 х + 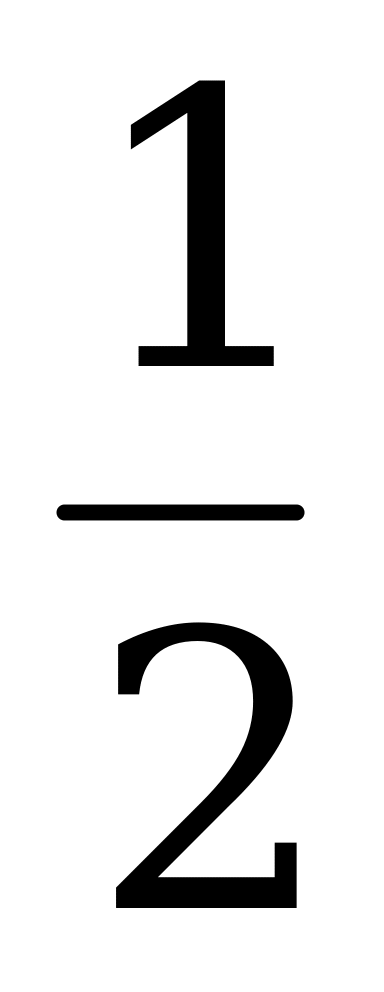 х + 7,494 х ) ∙ 0,3 –
х + 7,494 х ) ∙ 0,3 – 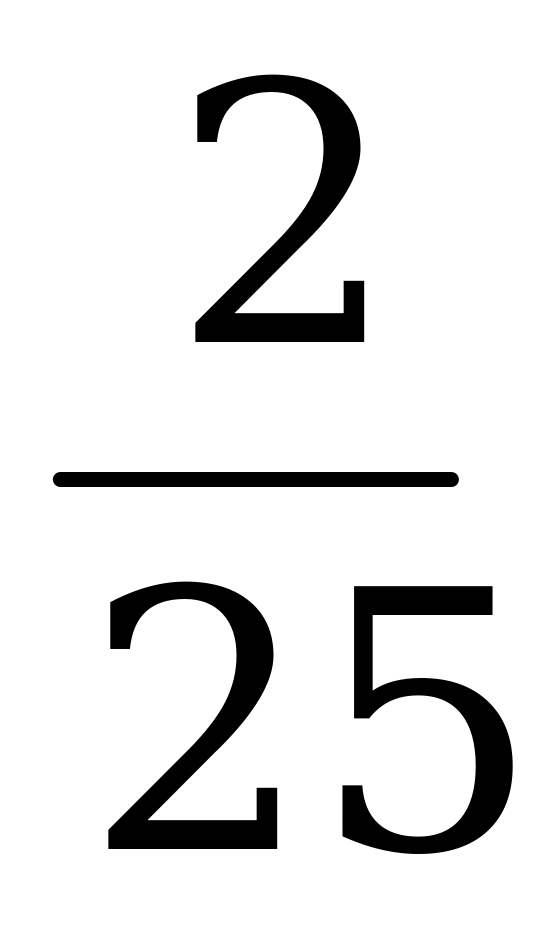 = 2,0024.
= 2,0024.
Ответ округлите до целого числа.

Вариант 1
Группа А
(Каждый правильный ответ – 1 балл)
Запишите в виде десятичной дроби число триста сорок восемь целых девять тысячных
Ответ: а) 348,9000; б) 348,009; в) 348,09; г) 348,9.
2. Представьте в виде неправильной дроби смешанное число 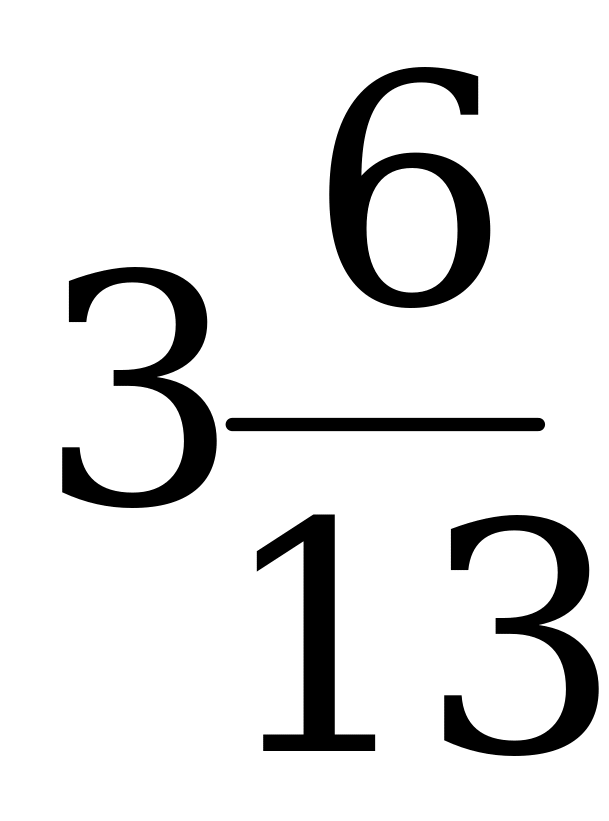
Ответ: а) 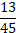 ; б)
; б) 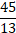 ; в)
; в) 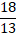 ; г)
; г) 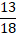
3. Выполните сложение: 3,6 + 2,14.
Ответ: а) 5,47; б) 2,50; в) 5,74; г) 2,05.
4. Выполните вычитание: 19,4 – 7,83.
Ответ: а) 11,57; б) 12,67; в) 12,43; г) 12,79.
5. Выполните вычитание: 26�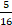 � - 3 �
� - 3 �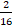 �
�
Ответ: а) 23; б) 23�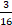 �; в)
�; в) 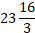 ; г)
; г) 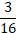 .
.
6. Найдите сумму дробей �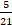 � и �
� и �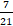 �
�
Ответ: а) 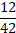 ; б)
; б) 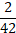 ; в)
; в) 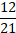 ; г)
; г) 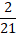 .
.
7. Выполните деление: 0,52 : 1,3
Ответ: а) 0,04; б) 4; в) 0,4; г) 0,31.
8. Выполните умножение: 12,1 ∙ 5,2
Ответ: а) 6,92; б) 62,92; в) 6,292 г) 629,2.
9. Найдите среднее арифметическое чисел 12 и 26.
Ответ: а) 19; б) 14; в) 24 г) 38.
10. Найдите корень уравнения 8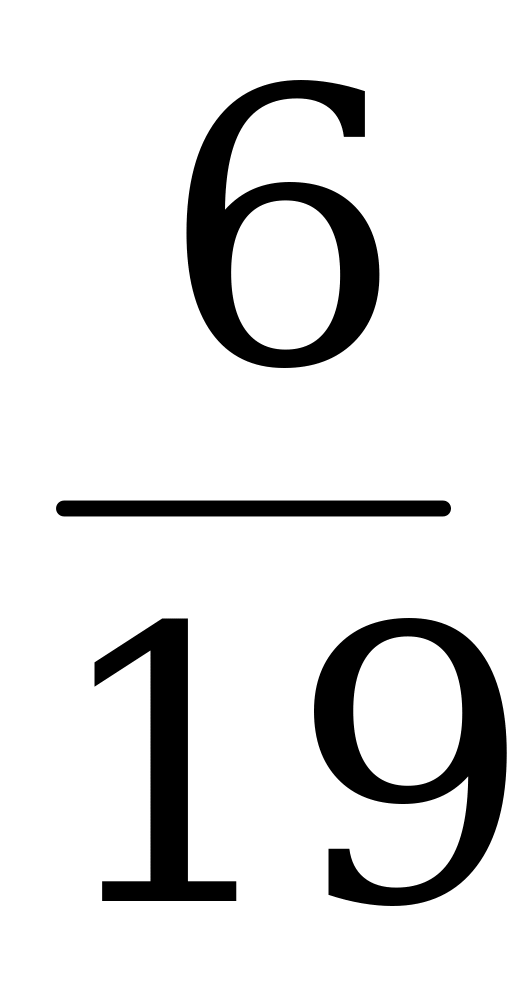 + х = 14
+ х = 14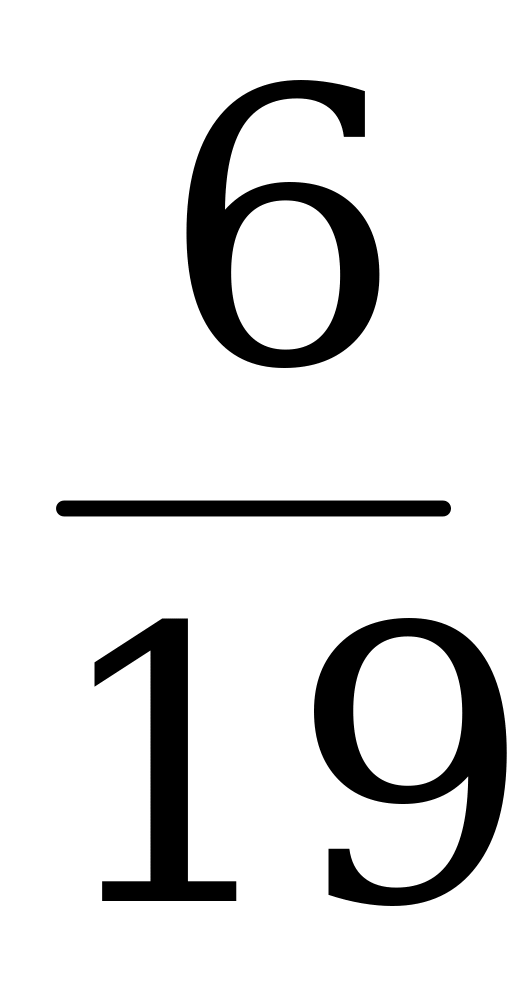 .
.
Ответ: а) 8; б) 6; в) 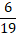 ; г) 14.
; г) 14.
Группа Б
(Каждое правильное и полное решение – 5 баллов)
11. Турист шел первые 3 часа пути со скоростью 4,6 км/ч, а затем 5 часов со скоростью 5,4 км/ч. Какова его средняя скорость?

12. Вычислите: ( 17,28 : 3,2 + 1,4 ∙ 2,5 ) : 8,9.

Группа В
(Каждое правильное и полное решение – 5 баллов)
13. Решите уравнение: ( 1,138 х + 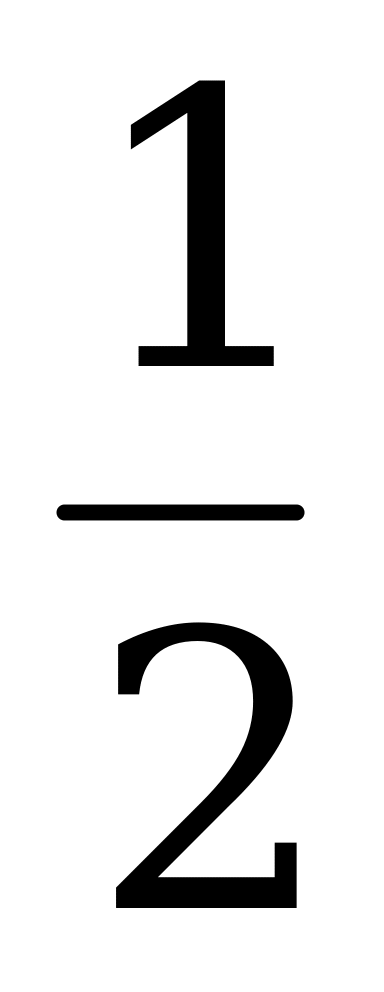 х + 1,212 х – 1,9) ∙ 0,2 +
х + 1,212 х – 1,9) ∙ 0,2 + 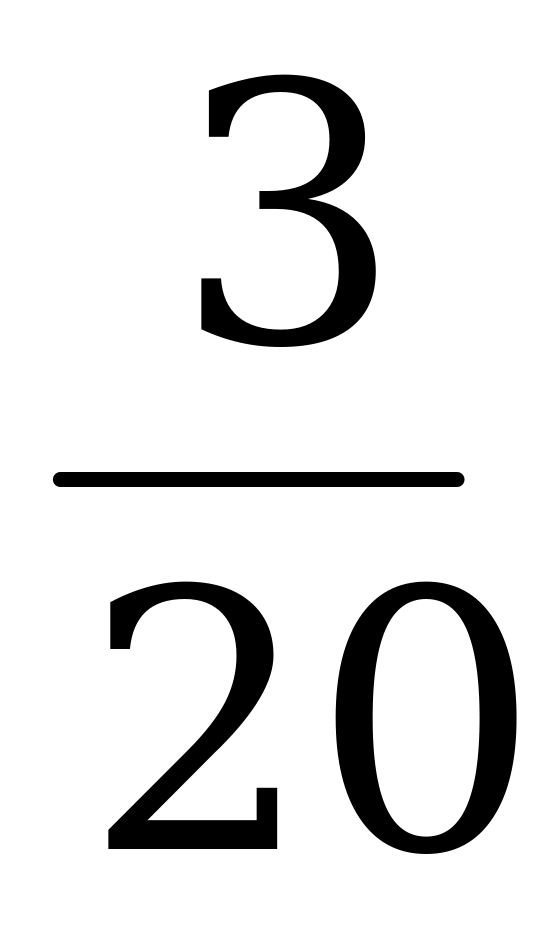 = 1,77.
= 1,77.
Ответ округли до целого числа.

Вариант 2
Группа А
(Каждый правильный ответ – 1 балл)
1. Запишите в виде десятичной дроби число четыреста пятьдесят восемь целых девять тысячных
Ответ: а) 458,9000; б) 458,009; в) 458,09; г) 458,9.
2. Представьте в виде неправильной дроби смешанное число 2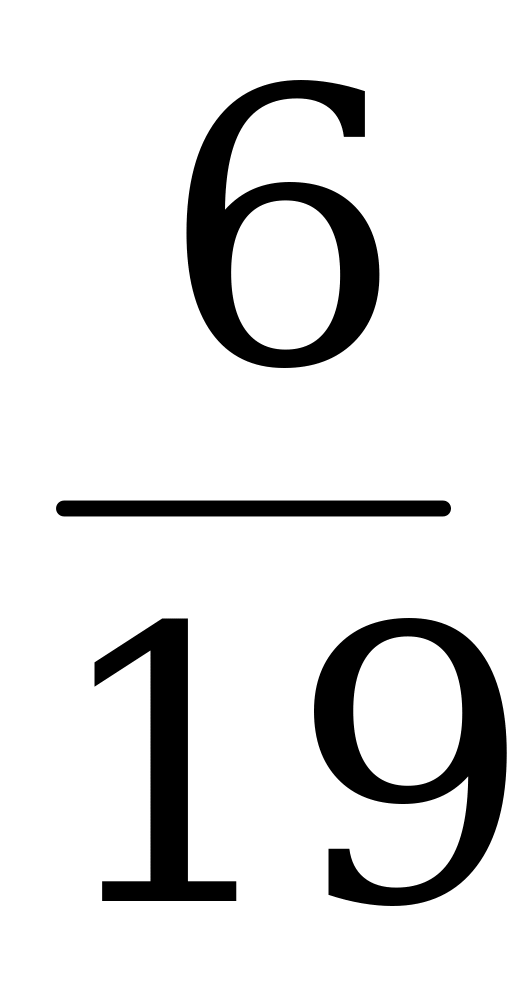
Ответ: а) 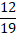 ; б)
; б) 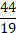 в)
в) 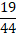 г)
г) 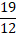
3. Выполните сложение: 4,6 + 3,24.
Ответ: а) 3,7; б) 7,30; в) 7,84; г) 8,84.
4. Выполните вычитание: 18,4 – 5,72.
Ответ: а) 3,88; б) 12,68; в) 126,8; г) 38,8.
5. Выполните вычитание: 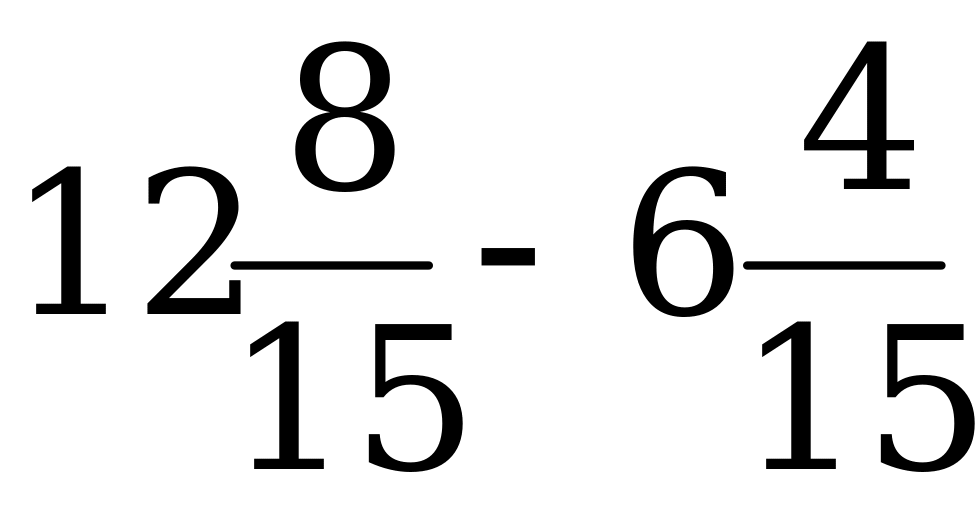
Ответ: а) 6; б) 6�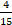 �; в)
�; в) 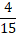 ; г) 6�
; г) 6�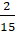 �
�
6. Найдите сумму дробей 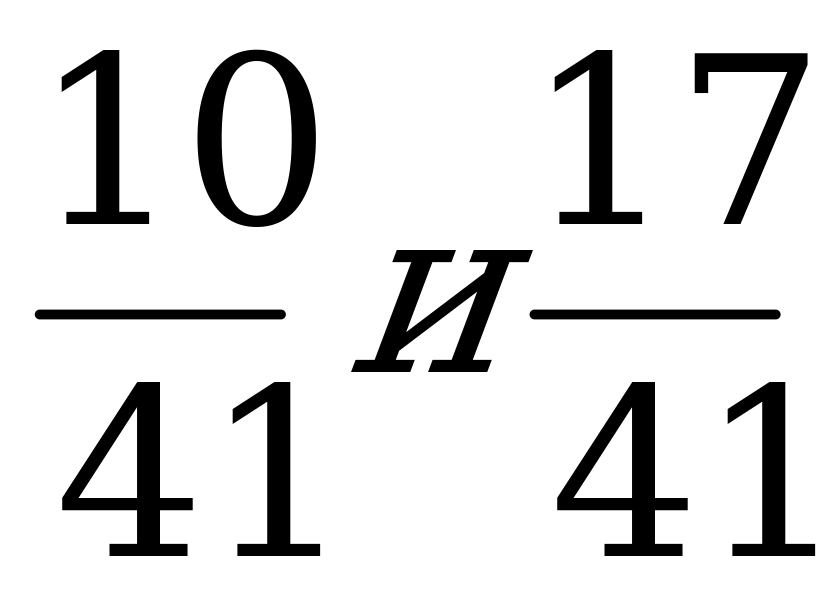
Ответ: а) 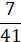 ; б)
; б) 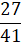 в)
в) 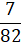 ; г)
; г) 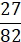 .
.
7. Выполните деление: 0,63 : 2,3
Ответ: а) 0,03; б) 3; в) 0,3; г) 0,31.
8. Выполните умножение: 11,2 ∙ 2,4
Ответ: а) 2,688; б) 26,88; в) 22,8 г) 22,88.
9. Найдите среднее арифметическое чисел 15 и 35.
Ответ: а) 50; б) 25; в) 35 г) 52.
10. Найдите корень уравнения 2�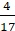 � + х = 14�
� + х = 14�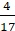 �
�
Ответ: а) 16; б) 12 в) 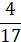 г)
г) 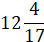 .
.
Группа Б
(Каждое правильное и полное решение – 5 баллов)
11. Турист шел первые 4 часа пути со скоростью 4,2 км/ч, а затем 3 часа со скоростью 4,9 км/ч. Какова его средняя скорость?

12. Вычислите: ( 32 – 132,3 : 12,6 ) ∙ 6,04 + 11,24

Группа В
(Каждое правильное и полное решение – 5 баллов)
13. Решите уравнение: ( 0,008 х + 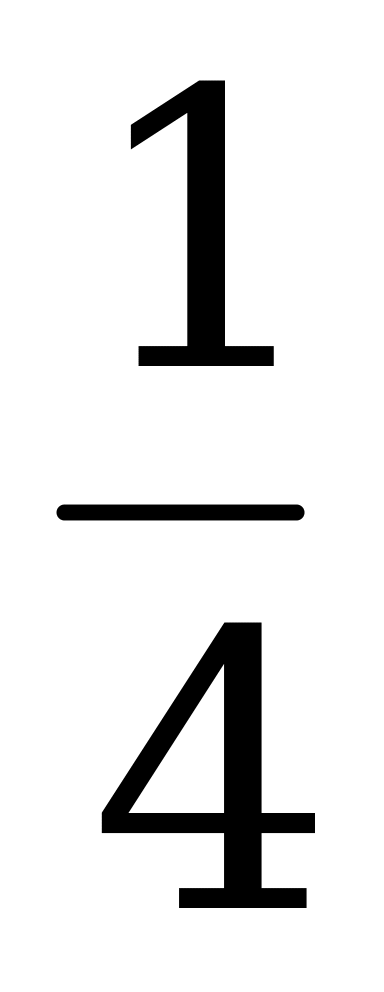 х + 5,692 х ) ∙ 0,2 –
х + 5,692 х ) ∙ 0,2 – 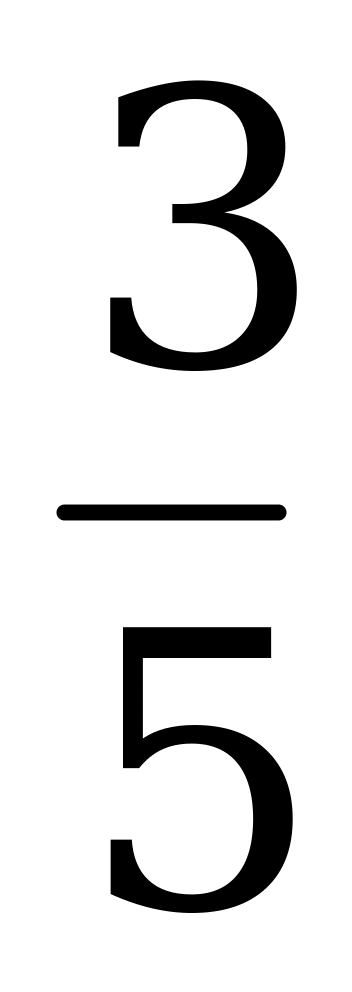 = 3,088.
= 3,088.
Ответ округли до целого числа.

Ответы:
Демонстрационный вариант:
| №п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| ответ | б | б | в | г | а | г | в | а | в | г | 5,04 км/ч | 30,2 | 1 |
Вариант1 и Вариант 2:
| №п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| В 1 | б | б | в | а | б | в | в | б | а | б | 5,1 км/ч | 1 | 4 |
| В 2 | б | б | в | б | б | б | в | б | б | б | 4,5 км/ч | 140 | 2 |




















