Программа внеурочной деятельности по математике 5-6 класс
«Изучение основ геометрии через практическое применение различных техник работы с геометрическими фигурами».
Составлена учителем математики МБУ «Гимназия 38» г.о.Тольятти
Тольятти 2017
Актуальность
Курс математики 5-6 классов, на мой взгляд, в большей степени направлен на изучение основ алгебры. Темам по геометрии отводится гораздо меньшее количество часов. Однако, в огромном количестве всевозможных востребованных профессий в современном обществе необходимы именно знания по геометрии. Поэтому внеурочная деятельность по математике в 5-6 классах может быть направлена именно на более широкое изучение геометрии, как основы многих современных профессий.
Изучение основ геометрии с использованием элементов творчества способствует не только формированию у обучаемых мотивации к дальнейшему освоению предмета, но и формированию компетенций, получению знаний, осваиванию умений и навыков в соответствии с требованиями к уровню подготовки выпускника современной школы, формированию не только заданных индивидуальных траекторий обучения, но и произвольных траекторий, определяемых обучаемым.
Данная программа может быть реализована в рамках методических рекомендаций при подготовке обучаемых к решению задач повышенной сложности и олимпиадных задач.
Кроме того, представленная программа дает возможность реализации всевозможных интегрированных мероприятий и проектов, а также вовлечения в педагогическую деятельность родителей обучаемых, что является немаловажным фактором современной педагогики.
Цель: формирование личностно ориентированных компетенций обучаемых в сфере практического применения теоретических знаний по геометрии.
Задачи:
- обеспечение эффективного сочетания разнообразных форм организации внеурочной деятельности по математике и взаимодействия всех ее участников;
-формирование образовательного базиса обучаемых, основанного не только на знаниях, но и на соответствующем культурном уровне развития личности, созданию необходимых условий для её самореализации;
-формирование у обучаемых навыков и умений применения полученных теоретических знаний по математике на практике;
-овладение геометрическим языком; развитие умения использовать его для описания предметов окружающего мира; развитие пространственных представлений, изобразительных умений, навыков геометрических построений;
- организация интеллектуальных и творческих соревнований, проектной и учебно-исследовательской деятельности, а также совместной работы с родителями.
Данный проект предлагается для реализации во внеурочной деятельности по математики обучающихся 5-6 классов. Основные методы проекта – это формирование компетенций обучающихся по геометрии через практическое применение и построение геометрических моделей, развитие комбинаторных и алгоритмических навыков обучающихся, создание благоприятной атмосферы для коллективной работы, разработка совместно с обучающимися собственных проектов и моделей.
Примерное тематическое планирование по реализации данного проекта:
| № п/п | Тема | Количество часов |
| 1 | Вводное занятие. | 2 |
| 2 | Задачи на клетчатой бумаге. | 4 |
| 3 | Пэчворк | 2 |
| 4 | Геометрические узоры. Паркетажи. | 4 |
| 5 | Пентамино. | 4 |
| 6 | Трудные задачи на разрезание. | 1 |
| 7 | Танграм. Рамки Никитина | 5 |
| 8 | Задачи на складывание из бумаги. Оригами. | 4 |
| 9 | Куб. Развертка куба. Модульные оригами. | 3 |
| 10 | Задачи с кубиками. Проекция. | 2 |
| 11 | Проектирование. Создание макетов. | 3 |
Методические рекомендации по некоторым темам проекта:
Вводное занятие.
На данном этапе необходимо поверхностно познакомить обучающихся с максимально возможными сферами деятельности человека, связанными с геометрией, а именно с геометрическими фигурами, их построением и т. д. Данная часть программы должна быть насыщена наглядным представлением всевозможных геометрических продуктов человеческой деятельности. Для этого используются разнообразные репродукции, фотографии, макеты и т.д., демонстрируемые с помощью презентаций и наглядных пособий. В качестве практического задания может быть предложена, например, техника рисования с использованием геометрических фигур или прямых линий. Данные занятия также могут проходить в рамках интегрированного урока, объединяющего математику и ИЗО. Можно посетить выставку, демонстрирующую работы по данной теме. В качестве домашнего задания может быть предложена совместная работа обучающих и родителей по созданию собственного творческого продукта по данной теме с последующей организацией выставки работ. Вводное занятие направлено на формирование мотивации к изучению всей программы в целом, выработки личностной заинтересованности обучающихся в предмете.
2.Задачи на разрезание на клетчатой бумаге.
Цель: Развитие представлений о симметрии, развитие комбинаторных навыков.
В начале изучения темы обучающимся предлагается самостоятельно разделить квадрат, состоящий из 16 клеток на две равные части различными способами, так, чтобы линия разреза шла по сторонам клеток. Т.е. задание носит поисковый характер. Затем совместно с обучающимися формулируется понятие симметрии.
Последующие задания по данной теме основаны на рассмотрении всевозможных вариантов задач на разрезания квадратов различной величины, а затем и различных фигур на равные части. Далее задания усложняются тем, что в разрезаемых фигурах должно быть еще и равное количество значков, изображенных на клеточке.
Пример:
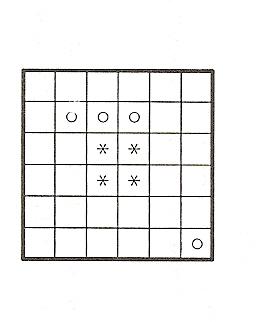
3. Геометрические узоры. Паркетажи.
Цель: Научиться покрывать плоскость различными фигурами (паркетажи могут быть с линиями разрыва или сплошными), или доказывать, что это невозможно.
Знакомство с данной темой начинается с введениея понятия орнамента или узора
Орна́мент (лат. ornemantum — украшение) — узор, основанный на повторе и чередовании составляющих его элементов; предназначается для украшения различных предметов.
Далее рассматриваются виды узоров с обязательной демонстрацией презентации, посвященной данной теме.
Примеры орнаментов:




Необходимо также на данном этапе ввести понятие равных фигур, актуализировать знания по теме симметрия, после чего обучаемым предлагается нарисовать эскиз паркета, состоящего из равных геометрических фигур. Домашним заданием может быть составление симметричного геометрического орнамента.
Затем рассматривается один из наиболее важных вопросов теории разбиения плоскости: «Какой формы должна быть плитка, чтобы ее копиями можно было покрыть плоскость без пробелов и двойных покрытий?» Доказывается, что существует только три правильных многоугольника, которыми можно покрыть плоскость. Это равносторонний треугольник, квадрат и шестиугольник.
Далее обучающимся предлагаются задачи на покрытие плоскости одинаковыми фигурами.
Третье занятие посвящено задачам о наиболее плотной укладке.
Следующее занятие знакомит обучаемых с творчеством Маурица Корнелиуса Эшера. Более подробно следует остановиться на темах:
-Мозаика
-Спирали
-Многогранники
-Невозможные фигуры (искаженные перспективы)
-Иллюзии
Вводимые понятия – перспектива, многогранник, спираль.
5.Геометрический конструктор. Пентамино.
Цель: развитие комбинаторных навыков учащихся.

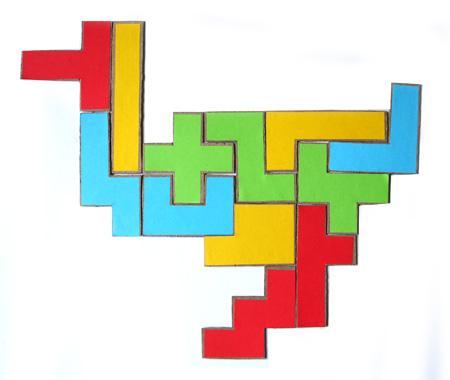
В данной теме дается понятие пентамино:
Пентамино́ (от др.-греч. πέντα пять, и домино) — пятиклеточные полимино, то есть плоские фигуры, каждая из которых состоит из пяти одинаковых квадратов, соединённых между собой сторонами («ходом ладьи»). Этим же словом иногда называют головоломку, в которой такие фигуры требуется укладывать в прямоугольник или другие формы.
Дается историческая справка, описывающая историю возникновения пентамино. Данная часть обязательно сопровождается презентацией, насыщенной всевозможными изображениями пентамино.
Затем предлагается обучающимся самостоятельно попробовать изобразить все возможные варианты фигур пентамино на клетчатой бумаге. Это может быть работа в группах, индивидуальное выполнение заданий. Далее проводится анализ всех получившихся фигур, фигуры вырезаются, подсчитывается их количество (12), определяются виды, и рассматривается вращение получившихся фигур, после чего вводится определение зеркальной симметрии и вращательной симметрии. Затем подводится общий итог первого занятия, заключающийся в определении общего количества фиксированных фигур пентамино:
5 × 8 + (1 + 4) × 4 + 2 + 1 = 63.

Последующие занятия по данной теме направлены на формирование компетентности у обучающихся по следующим направлениям:
-умение рисовать простые геометрические фигуры на клетчатой бумаге, состоящие из всевозможных вариантов фигур пентамино.
-умение укладывать всевозможные фигуры из пентамино, в том числе и фигуры с отверстиями.
Предлагается также решить ряд задач с использованием фигур пентамино. Для этого одно занятие можно посвятить изготовлению данных фигур из картона.
В конце изучения данной темы целесообразно провести какое-либо обобщающее мероприятие, где будут задействованы не только обучающиеся, но и их родители, например, это может быть выставка работ, либо турнир по пентамино.
6. Трудные задачи на разрезание.
Тема: Задачи на разрезание фигур более сложной формы с границами, являющимися дугами.
Цель: Научиться разрезать фигуры более сложной формы с границами, являющимися дугами, и составлять из полученных частей квадрат.
На занятиях по данной теме решаются задачи с использованием клетчатой бумаги и ножниц. В качестве итогового задания может быть предложено составить аппликацию, изображающую какое-либо архитектурное сооружение.
7.Танграм.
Цель: знакомство с геометрическим исследованием и конструированием. Развитие комбинаторных навыков.
Введение понятия танграмм:
Танграм (кит.七巧板, пиньинь qī qiǎo bǎn, букв. «семь дощечек мастерства») — головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.). Фигура, которую необходимо получить, при этом обычно задаётся в виде силуэта или внешнего контура. При решении головоломки требуется соблюдать два условия: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны накладываться друг на друга.
Далее - исторический аспект с обязательной демонстрацией наглядных пособий.


Затем обучающимся предлагается самостоятельно начертить на плотной бумаге, а затем вырезать таграм. После чего проговаривается число фигур, входящих в танграм и их название. Далее обучающиеся самостоятельно складывают различные фигурки из частей танграма. В качестве домашнего задания может быть предложено сложить фигурку животного из частей танграма, используя разноцветную бумагу и наклеить ее на картон (в качестве шаблона используются части танграма, вырезанные на уроке).
Следующее занятие по данной теме носит поисково-эвристический характер. Здесь разбираются парадоксы танграма.


Обучающимся дается задание попробовать сначала доказать, а потом разрешить данный парадокс.
Третье занятие проводится с использованием текстового редактора Microsoft Word, где обучающиеся сначала создают шаблоны фигур, входящих в танграм, а затем складывают всевозможные фигурки из них. Можно также воспользоваться программой "Графические диктанты и Танграм"
Итоговое занятие по данной теме может быть посвящено созданию обучающимися совместной аппликации, созданной из фигур танграма, либо это может быть рисунок, созданный в графическом редакторе.
8. Задачи на складывание из бумаги. Оригами. Оригами треугольных модулей.
На первом занятии рассматривается история возникновения оригами, виды и техники оригами, изучается система знаков. Вводятся понятия – равные углы, равные части. Актуализируются знания по теме симметрия, равные фигуры.
Примеры условных знаков:
 Равные углы
Равные углы

Сгиб долиной, линия сгиба долиной.



Следующее занятие – это создание обучающимися собственного творческого продукта. Здесь может быть организована работа в группах или индивидуальная, выбор можно оставить за учениками. Можно использовать письменную рефлексию в виде тестирования, состоящего из 2-3 вопросов на начальном и конечном занятии для подведения промежуточных итогов. В качестве домашнего задания можно предложить подготовить доклад о связи математики и оригами в современном мире или предложить провести анализ применения оригами в прошлом, настоящим и рассмотреть возможные перспективы развития оригами в будущем.
Третье занятие – это создание фигур с помощью треугольных модулей. На данном этапе вводится понятие множества, проводится актуализация знаний по темам сумма углов треугольника и прямоугольный треугольник. Обучаемым предлагается самостоятельно создать несложную фигуру из треугольных модулей. Кроме того, можно предложить обучающимся самим попробовать придумать какие-то свои виды модулей для создания фигур оригами, тем самым создать возможность научиться анализировать, систематизировать и обобщать пройденный материал, а также создавать собственный продукт, основанный на самостоятельно разработанной концепции. Эта работа может послужить основой исследовательской работы по данной теме.

Оценка рисков
Финансовые – материально-техническое и учебно-методическое обеспечение реализации проекта
Социально-демографические (недостаточно подготовленные или отсутствие кадров, отрицательная демографическая статистика для определенных территориальных областей)
Нормативно-правовые( реализация проекта может столкнуться с отсутствиями государственными нормативно-правовыми документами)
Краткосрочные результаты – положительная динамика рефлексии, развитие компетенций обучающихся в области практического применения теоретических знаний по геометрии (развитие комбинаторных навыков, умение самостоятельно строить алгоритм работы, умение применять на практике знания по проектированию геометрических моделей) , повышение мотивации к изучению математики, повышение уровня сплоченности детского коллектива, создание благоприятной атмосферы взаимодействия с родительским коллективом, разработка методических рекомендаций по реализации и оснащению проекта.
Долгосрочные результаты:
- разработка новых методик или технологий, внедренных в рамках проекта;
-дополнение проекта методическими рекомендациями, а также результатами оценки эффективности реализации проекта;
- расширение программы за счет дополнения тем, подходящих для более старшей возрастной категории обучающихся.
Нормативно-правовая база
1.Федеральный закон от 01.09.2013г. N 273-ФЗ "Об образовании в Российской Федерации"
2. Постановление Правительства Самарской области от 29.11.2013 №700 "Об утверждении государственной программы Самарской области "Развитие образования и повышение эффективности реализации молодежной политики в Самарской области" на 2014-2020 годы"
3.Основная образовательная программа муниципального бюджетного общеобразовательного учреждения гимназии №38 городского округа Тольятти.
4.Единая коллекция цифровых образовательных ресурсов. http://school-collection.edu.ru
5.Научная электронная библиотека. http://elibrary.ru/defaultx.asp
6. Шарыгин И.Ф., Ерганжиева Л.Н.: Наглядная геометрия. 5-6 классы. Пособие для общеобразовательных учреждений: Дрофа, 2014г.
Программа внеурочной деятельности по математике 5-6 класс «Изучение основ геометрии через практическое применение различных техник работы с геометрическими фигурами».
| Содержание программы | Кол-во часов | Формы / методы | Планируемые предметные результаты | Используемые УУД |
| Раздел 1. Геометрический мир человека. |
| 1 Геометрия в жизни человека
| 1 | Индивидуальная, фронтальная и групповая работа/ наглядный, словесный, анализ, самоанализ, рефлексия. | Формирование представлений учащихся о геометрии как о методе познания действительности через творчество
| Познавательные УУД: анализировать продукт деятельности других людей; сравнивать, классифицировать объекты по выделенным признакам; выдвигать гипотезы и обосновывать их; строить логические рассуждения; самостоятельное выделение и формулирование познавательной цели; структурирование знаний; постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера; Регулятивные УУД: умение определять цель работы и планировать конечный результат; умение осуществлять коррекцию (внесение необходимых дополнений и корректив в план) умение осуществлять саморегуляцию, как способ к мобилизации сил и энергии; Коммуникативные УУД: умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникаций, владение монологической и диалогической формами речи; планирование учебного сотрудничества с учителем и сверстниками — определение целей, функций участников, способов взаимодействия; Личностные УУД: установление учащимися связи между целью изучения геометрии и его мотивом; |
| Раздел 2. Пространство и плоскость |
| 2. Пространство и размерность | 1 | Урок-исследование/ наглядный, словесный, анализ, самоанализ, рефлексия. | Научиться определять пространство и его размерность, знать понятие перспективы, уметь изображать простейшие объемные геометрические фигуры
| Познавательные УУД: умение пользоваться информационными источниками, как средством получения необходимой информации; осознанное и произвольное построение речевого высказывания в устной форме; самостоятельное создание алгоритмов деятельности при решении задач творческого и поискового характера; выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; развитие комбинаторных навыков и умение применять их на практике; умение анализировать ситуацию; умение сравнивать и классифицировать объекты по определенным признакам; умение рассуждать логически, устанавливать причинно-следственные связи, выдвигать и доказывать гипотезы; Регулятивные УУД: умение выделять цель работы, планировать и прогнозировать результат своих действий; умение адекватно оценивать свои действия и, в случае необходимости, корректировать план и способы выполнения поставленной задачи; развивать способность к саморегуляции и умение преодолевать препятствия; Коммуникативные УУД: умение сотрудничать с учителем и сверстниками; умение действовать совместно с коллективом, с достаточной точностью и полнотой выражая свои мысли; умение грамотно и четко осуществлять постановку вопросов, контролировать и оценивать действия партнера; умение объективно выявлять причины конфликта, оценивать его и находить альтернативные способы выхода из конфликта; |
| 3.Простейшие геометрические фигуры.
| 2
| Фронтальные, групповые | Научиться строить простейшие геометрические фигуры с помощью геометрических инструментов, научиться находить вертикальные и смежные углы |
| 4. Конструирование из «Т»
| 1 | Эвристический метод обучения, групповое занятие | Научиться складывать различные фигуры из буквы Т, а также заполнять пространство на клетчатой бумаге буквами Т |
| 5. Задачи на разрезание и складывание фигур.
| 2 | Индивидуальная работа, работа в группах/ наглядный, словесный, анализ, самоанализ, рефлексия. | Научиться разделять различные фигуры на клетчатой бумаге на равные части, научиться разрезать фигуры более сложной формы с границами, являющимися дугами, и составлять из полученных частей квадрат.
|
| 6. Пентамино.
| 3 | Исследование, урок-игра, работа в группах, индивидуальная работа/ анализ, самоанализ, рефлексия | Понять принцип образования фигур пентамино, уметь изображать фигуру, симметричную данной научиться заполнять плоскость фигурами пентамино |
| Раздел 3. Геометрия фигур на плоскости и в пространстве. |
| 7. Геометрические головоломки.
| 2 | Работа по карточкам, урок-соревнование, работа в группах/ | Знать понятие правильных многогранников, познакомиться с названиями некоторых правильных многогранников и их развертками на плоскости, уметь решать задачи на разрезание плоских фигур | Познавательные УУД: умение анализировать полученную информацию и применять ранее полученные знания при изучении новой темы; умение сравнивать объекты и классифицировать их по выделенным признакам; умение самостоятельно устанавливать причинно- следственные связи между объектами изучения , строить логические рассуждения, выдвигать и доказывать гипотезы; умение моделировать по образцу, а также преобразовывать модели; умение самостоятельно создавать алгоритм деятельности при выполнении заданий творческого характера; Регулятивные УУД: умение ставить перед собой цель , планировать и прогнозировать результат своих действий; умение осуществлять самоконтроль, объективно оценивать ситуацию и корректировать свои действия по мере необходимости; умение контролировать свое поведение, мобилизируя силы и энергию при преодолении препятствий; Коммуникативные УУД: умение сотрудничать с учителем и сверстниками, определяя цели, функции участников образовательного процесса и способов взаимодействия между ними; инициативное сотрудничество в поиске и сборе информации; умение объективно контролировать, корректировать и оценивать действия партнера; Личностные УУД: умение оценивать усваиваемое содержание со стороны нравственно — этической точки зрения. |
| 8. Геометрия танграма.
| 3 | Индивидуальная и фронтальная работа, работа в группах, интегрированный урок (создание собственных картин из танграма последующей выставкой работ) | Познакомиться с геометрическим исследованием и конструированием, развить комбинаторные навыки, научиться решать задачи, связанные с древней китайской головоломкой «Танграм» , уметь составлять фигуры из частей стомахиона как по образцу, так и самостоятельно
|
| 9.Стомахион | 1 | Урок-турнир |
| 10. Задачи на раскраску. | 2 | Фронтальная, индивидуальная, групповая работа/ анализ, синтез, самоанализ, рефлексия | Научиться доказывать, что некоторые задачи на разрезание не имеют решения, с помощью правильно подобранной раскраски ( для решения предлагаются самые простые задачи по данной теме) |
| 11. Геометрический тренинг | 1 | Урок-исследование на местности, работа в группах | Научиться самостоятельно находить и замечать различные особенности геометрических фигур и делать выводы из замеченных особенностей, научиться видеть геометрические фигуры в окружающем мире, уметь проводить простейшие измерения и вычисления площади этих фигур |
| Раздел 4. Геометрия эксперимента. |
| 12. Топологические опыты
| 2 | Урок -исследование | Иметь представление о топологии, как об одном из разделов геометрии, освоить некоторые топологические опыты | Познавательные УУД: умение анализировать, сравнивать и квалифицировать объекты по определенным признакам, устанавливать причинно-следственные связи между объектами; умение создавать модели по предложенному алгоритму и самостоятельно создавать собственные алгоритмы деятельности при решении проблем творческого характера, опираясь на ранее полученные знания; Регулятивные УУД: умение грамотно планировать свои действия, а также прогнозировать результат собственной деятельности; умение вносить коррективы в процесс деятельности и объективно оценивать результат; умение применять волевые усилия при возникновении сложной ситуации в работе; уметь самостоятельно контролировать своё время и управлять им; принимать решения в проблемной ситуации на основе переговоров; Коммуникативные УУД: умение продуктивно взаимодействовать со сверстниками и взрослыми; умение адекватно оценивать ситуацию, предлагая альтернативные способы выхода из конфликта, в случае его возникновения; формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности; Личностные УУД: умение отстаивать свою точку зрения, выражая понятно и точно свои мысли, не затрагивая при этом честь и достоинство своего оппонента; позитивное отношение к участникам совместной деятельности;
|
| 13. Задачи со спичками | 1 | Урок-игра | Научиться решать задачи со спичками |
| 14. Задачи, головоломки, игры. | 2 | Урок – игра в разведчиков ( расшифровка посланий); работа в группах | Познакомиться со способом шифровки, научиться решать геометрические головоломки, используя уже имеющиеся знания по геометрии |
| 15. Опыты с листом бумаги. | 1 | Работа в группах, индивидуальная работа | Научиться вырезать фигуры из бумаги, не используя геометрические приборы |
| 16. Задачи на складывание из бумаги. | 1 | Работа в группах, индивидуальная и фронтальная работа | Знать и уметь строить координатные оси, научиться решать задачи на складывание из бумаги |
| 17. Оригами. | 2 | Индивидуальная работа, работа в группах, конкурс на лучшую поделку | Научиться, используя схему складывать фигурки из прямоугольного листа бумаги, научиться понимать условные обозначения на элементарных чертежах |
| 18. Модульные оригами. | 2 | Работа в группах, урок-«конструкторское бюро» | Научиться изготавливать объемные фигурки из одинаково сложенных прямоугольных листов бумаги (модулей) |
| Раздел 5. Геометрия в искусстве. |
| 19.Симметрия | 2 | Фронтальная работа, индивидуальные карточки, групповая работа | Знать понятие симметрии, уметь строить фигуры, симметричные данным относительно заданной оси симметрии | Познавательные УУД: умение осуществлять анализ объектов с выделением существенных и несущественных признаков; умение осуществлять синтез, как составление целого из частей; умение создавать модели по предложенному алгоритму, а также создавать собственный алгоритм изготовления новых моделей; Регулятивные УУД: умение ставить перед собой цель, планировать и прогнозировать результат своих действий; формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности; Коммуникативные УУД: умение эффективно взаимодействовать со сверстниками, умение сотрудничать и грамотно отстаивать свою точку зрения Личностные УУД: Позитивное отношение к участникам совместной деятельности
|
| 20.Бордюры | 1 | Индивидуальная и фронтальная работа | Умение создавать свои трафареты из листа бумаги, используя симметрию, умение определять центр симметрии |
| 21. Разбиение плоскости.
| 2 | Индивидуальна, фронтальная и групповая работа/анализ, самоанализ | Умение разбивать плоскость на одинаково закрашенные участки, выделяя элементарную ячейку(паркетажи) |
| 22. Орнаменты.
| 2 | Урок - «творческая мастерская», работа в группах. | Умение создавать собственные орнаменты, знакомство с творчеством М. Эшера , а также народными орнаментами |



















 Равные углы
Равные углы














