Конспект урока по математике
для 6 класса на тему:
«Сложение и вычитание
Положительных и отрицательных чисел».
Тип урока: обобщающий урок.
Цели урока: Образовательная цель:
- закрепить изученные понятия, научить применять и пользоваться полученными знаниями;
- продолжить формирование навыков работы с целыми числами;
- познакомить учащихся с некоторыми фактами из истории математики, привить интерес к науке.
Воспитательная цель: - воспитание нравственных качеств личности, таких как ответственность, аккуратность, дисциплинированность;
- воспитание культуры общения.
Развивающая цель: - развитие у учащихся умений выделять главное, существенное в изучаемом материале, обобщать изучаемые факты, логически излагать свои мысли;
- развитие психических процессов, таких как память, внимание, мышление, а также наблюдательности, активности, самостоятельности.
Требования к ЗУНам учащихся:
Учащиеся должны знать:
- правило сложения отрицательных чисел;
- правила сложения и вычитания чисел с разными знаками;
- имена великих ученых-математиков, сделавших вклад в развитие теории чисел.
Учащиеся должны уметь:
- применять правила при выполнении упражнений.
Оборудование: мультимедиа-проектор, компьютер, рабочие листы, карточки с заданиями, тесты, листы с домашним заданием.
Организационный период:
- подготовка выступлений троих учащихся (правила в стихах );
- оформление презентации
План урока:
-
Организационный момент, постановка цели - 2 мин.
-
Историческая справка – 5 мин
-
Разминка – «Вспомни правила», дидакт. игра «Реши и прочти» – 8 мин.
-
Реши задание №1 ВПР положительные и отрицательные числа по 3 каж ученик
-
.баланс телефона, прибыль или убыток фирма
-
.география температура воздуха
-
Постановка домашнего задания - 1 мин.
-
Подведение итогов – 2 мин.
На парте у каждого ученика лежит рабочий лист (приложение 1).
Ход урока:
-
Организационный момент. Постановка цели.
Учитель приветствует учащихся, проверяет готовность помещения к уроку.
(Слайд №1 с темой)
Ребята, сегодня мы с вами завершаем изучение темы «Сложение и вычитание положительных и отрицательных чисел». Урок сегодня немного не обычный – в виде игры, но это не значит, что нужно расслабиться и ничего не делать. У каждого есть шанс заработать две хорошие оценки. А для этого вы должны быть активны и внимательны. Решать по цепочке ВПР задание№1 Перед каждым на парте лежит чистый лист – черновик и рабочий лист с таблицами к заданиям. По ходу урока вы должны будете их заполнить.
Вы знаете как выглядят отрицательные числа, где они расположены на координатной прямой. А знаете ли Вы когда и где они применяются ? Сегодня на уроке мы постараемся в этом разобраться. Но для этого вам нужно будет применить все свои знания по выше названной теме.
(Слайд №3 с эпиграфом)
-
Историческая справка.
Известно, что натуральные числа возникли при счете предметов. Потребность человека измерять величины и то обстоятельство, что результат измерения не всегда выражается целым числом, привели к расширению множества натуральных чисел. Были введены нуль и дробные числа. Процесс исторического развития понятия числа на этом не закончился. Однако не всегда первым толчком к расширению понятия числа были исключительно практические потребности людей. Бывало и так, что задачи самой математики требовали расширения понятия числа.
Именно так обстояло дело с возникновением отрицательных чисел. Понятие об отрицательных числах возникло в практике решения алгебраических уравнений.
После расширения множества натуральных чисел до дробных стало возможным делить любое целое число на другое целое число (за исключением деления на нуль). Вычитать же целое число из другого целого числа, когда вычитаемое больше уменьшаемого, долгое время казалось невозможным. Однако при решении уравнений нередко приходилось производить вычитание большего числа из меньшего и сталкиваться таким образом с понятием отрицательного числа.
Не только египтяне и вавилоняне, но и древние греки не знали отрицательных чисел. Понятие отрицательного числа появляется при решении систем линейных уравнений. Для производства вычислений математики того времени пользовались счетной доской, на которой числа изображались с помощью счетных палочек. Так как знаков + и — в то время еще не было, палочками красного цвета изображали положительные числа, отрицательные же — палочками черного цвета. Отрицательные числа долгое время называли словами, которые означали «долг», «недостача». Даже в VII в. в Индии положительные числа толковались как имущество, а отрицательные — как долг. В древнем Китае были известны лишь правила сложения и вычитания положительных и отрицательных чисел; правила умножения и деления не применялись.
Еще в III в. древнегреческий математик Диофант фактически уже пользовался правилом умножения отрицательных чисел.
Отдельно взятые отрицательные числа Диофант не признавал и, если при решении уравнения получался отрицательный корень, то он отбрасывал его как «недопустимый». Диофант старался так формулировать задачи и составлять уравнения, чтобы избегать отрицательных корней.
Совершенно по-иному относились к отрицательным числам индийские математики. Они признавали существование отрицательных корней уравнений, толковали положительные числа как представляющие имущества, а отрицательные — долги, применяя к ним все правила четырех действий, однако без должного теоретического обоснования.
-
Разминка – «Вспомни правила», дидактическая игра «Реши и прочти» (устно).
Ребята, давайте вспомним правила, с которыми вы познакомились на предыдущих уроках.
А сделаем мы это необычно - в стихах:
1-ый ученик:
Числа отрицательные, новые для нас,
Лишь совсем недавно изучил наш класс.
Сразу поприбавилось всем теперь мороки –
Учат – учат правила дети все уроки.
2-ой ученик:
Если уж захочется вам сложить
Числа отрицательные, нечего тужить:
Надо сумму модулей быстренько узнать,
К ней потом знак «минус» взять да приписать.
3-ий ученик:
Если числа с разными знаками дадут,
Чтоб найти их сумму, все мы тут как тут.
Больший модуль быстро очень выбираем.
Из него мы меньший вычитаем.
Самое же главное – знак не позабыть!
- Вы какой поставите? – мы хотим спросить
- Вам секрет откроем, проще дела нет,
Знак, где модуль больше, запиши в ответ.
) Хорошо. Правила вы знаете, а умеете ли вы их применять? Сейчас мы это узнаем.
Необходимо по порядку выполнить 11 заданий, вписать ответы в таблицу на рабочем листе и упорядочить полученные числа по возрастанию.
| I II III IV V VI VII VIII IX X XI | Найти сумму -8 и 5 Найти сумму -12 и 5 Найти сумму -100 и 100 Найти модуль -38 Найти модуль суммы -10 и 5 Найти разность -13 и 7 Найти разность 40 и 90 Найти разность -400 и 50 Найти сумму -25 и -34 Найти разность -120 и -20 Найти сумму 56 и -110 | У Г П А Т А М Б А Р Х |
Итак, называем свои ответы по цепочке, начиная с первой парты первого ряда.
(Учащиеся решают примеры устно и одновременно записывают ответы в таблицу на рабочем листе.)
Ответы:
| У | Г | П | А | Т | А | М | Б | А | Р | Х |
| -3 | -7 | 0 | 38 | 5 | -20 | -50 | -450 | -59 | -100 | -54 |
Прошу одного ученика упорядочить числа по возрастанию
(Учащиеся упорядочивают числа по возрастанию.)
Ответ:
| Б | Р | А | Х | М | А | Г | У | П | Т | А |
| -450 | -100 | -59 | -54 | -50 | -20 | -7 | -3 | 0 | 5 | 38 |
Итак, загадано слово – БРАХМАГУПТА. Вы конечно же узнали имя индийского математика Брахмагупты, который жил в VII в. и один из первых стал использовать положительные и отрицательные числа. Положительные числа этот математик представлял как «имущество», а отрицательные числа – как «долги». Вот правила сложения и вычитания, изложенные индийским математиком Брахмагуптой:
|
| Современная запись | Правила Брахмагупты |
| 1. 2. 3. 4. 5. 6. 7. 8. | a + b = c (- a) + (- b) = - c a + (- b) = a – b a + (- a) = 0 0 + (- a) = - a 0 + a = a 0 – (- a) = a 0 – a = - a | Сумма двух имуществ есть имущество. Сумма двух долгов есть долг. Сумма имущества и долга равна их разности. Сумма имущества и равного долга равна нулю. Сумма нуля и долга есть долг. Сумма нуля и имущества есть имущество. Долг, вычитаемый из нуля, становится имуществом. Имущество, вычитаемое из нуля, становится долгом. |
Постарайтесь перевести правила Брахмагупты на современный язык.
(Примерный ответ учащихся:
-
Сумма двух положительных чисел – число положительное.
-
Сумма двух отрицательных чисел - число отрицательное.
-
Сумма положительного и отрицательного числа равна их разности.
-
Сумма противоположных чисел равна нулю.
-
Сумма положительного числа и нуля есть само число.
-
Сумма отрицательного числа и нуля есть само число.
-
Если из нуля вычесть отрицательное число, то получится число положительное.
-
Если из нуля вычесть положительное число, то получится число отрицательное.)
Однако, несмотря на широкое использование отрицательных чисел при решении задач они долгое время не получали признания. Не одобряли их долго и европейские математики, потому что истолкование «имущество — долг» вызывало недоумения и сомнения. В самом деле, можно «складывать» или «вычитать» имущества и долги, но какой реальный смысл может иметь «умножение» или «деление» имущества на долг?
Вот почему с большим трудом завоевывали себе место в математике отрицательные числа.
-
В жизни Баланс телефона и прибыль или убыток фирмы приложение 2
-
В географии
-
Дидактическая игра «Поле чудес».
Следующая игра, в которую мы поиграем – это «Поле чудес». Для того, чтобы отгадать фразу, вы снова должны вспомнить правила сложения отрицательных чисел, чисел с разными знаками и применив их решить примеры.(учитель раздает каждому ученику карточку с 6-тью примерами. (приложение 3) Всего вариантов карточек 5: примеры 1-6, 7-12, 13-18, 19-24, 25-30.) Решив примеры, напротив каждого ответа поставьте букву, ему соответствующую.) Для этого воспользуйтесь таблицей 3 на рабочем листе:
| А | Б | Д | е | ж | и | к | м | о | п | р | с | т | у | ь | ч |
| -7,6 | 9,3 | -3,5 | -6,1 | -9,2 | -5,4 | -2,9 | 8 | -8 | -5,2 | -42 | 5,7 | 0 | -8,3 | 5,3 | -9,6 |
Учащиеся решают примеры на черновике, ответы записывают на карточки, напротив каждого ответа – соответствующую букву.)
Что же получилось? (Слайд №24, 1 часть)(Учащиеся по порядку называют ответ и соответствующую букву.)Получили: ПОДРУЖИСЬ С МАТЕМАТИКОЙ УДАЧИ ТЕБЕ! Ну что же, победа за вами!
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| п | о | д | р | у | ж | и | с | ь | с | м | а | т | е | м | а | т | и | к | о |

| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| й | у | д | а | ч | и | т | е | б | е |
Отрицательные числа довольно долго
-
Постановка домашнего задания.
Ваше домашнее задание будет необычным. Каждый из вас получит по карточке. Задача: решить примеры, результаты упорядочить по убыванию и получить слово, которое будет являться ответом на поставленный вопрос.
-
Подведение итогов.Итак, сегодня на уроке мы завершили изучение темы «Сложение и вычитание положительных и отрицательных чисел». Теперь вы немного узнали историю отрицательных чисел и где они применяются и смело можете переходить к умножению и делению отрицательных чисел. Удачи вам!
Фамилия, имя_______________________________
-
Реши и прочти.
Расположи полученные числа по возрастанию.
-
Поле чудес.
| А | Б | Д | е | ж | и | к | м | о | п | р | с | т | у | ь | ч |
| -7,6 | 9,3 | -3,5 | -6,1 | -9,2 | -5,4 | -2,9 | 8 | -8 | -5,2 | -42 | 5,7 | 0 | -8,3 | 5,3 | -9,6 |
Задания: 5 вариантов.
-
- 3,4 + (- 1,8) -
– 3,2 + (- 4,8) -
-11,3 + 7,8 -
-37 + (- 5) -
- 4,8 + (- 3,5) -
-4,5 + (- 4,7)
| -
1,6 + (- 1,6) -
– 9,6 + 3,5 -
16,3 + (- 8,3) -
– 4,9 + (- 2,9) -
– 9,2 + 9,2 -
4,6 + (- 10)
| -
– 14,5 + 4,9 -
-13,7 + 8,3 -
37,1 + (-37,1) -
– 2,7 + (- 3,4) -
15,1 + (- 5,8) -
11,4 + (-17,5)
|
-
-0,5 + (- 4,9) -
– 21,4 + 27,1 -
– 11,3 + 16,6 -
15 + (- 9,3) -
- 4,1 + 12,1 -
- 3,5 + (- 4,1)
| -
– 13,8 + 10,9 -
3,2 + (- 11,2) -
– 18 + 12,6 -
– 19,1 + 10,8 -
- 7,1 + 3,6 -
– 18,5 + 10,9
|
|
вместо * цифры чтобы было верное равенство
| 1 вариант | 2 вариант |
| 1) -3 + * = -8 | 1) * + (-12) = -17 |
| 2) * + 5 = -10 | 2) -18 + * = -9 |
| 3) 25,3 + * = 19,1 | 3) * + (-8,4) = 15,2 |
| 4) * - 6,8 = -4,5 | 4) 4,3 — *= -5,5 |
| 5) -21 : * = 7 | 5) -35 : * = 5 |
|
|
|
Применение положительных и отрицательных чисел в географии
1) Термометры Посмотрим на шкалу обычного уличного термометра.
Она имеет вид, изображенный на шкале 1. Найдите значение температуры в селе, определите, как изменилась температура
| месяц город | январь | июнь | Вывод (как изменилась температура, на сколько?) | Февраль | август | Вывод (как изменилась температура, на сколько?) | январь | февраль | Вывод На сколько изменилась? |
| Орта тюбе | -10 | 38 | 38- (-10)=48 0С | -12 | 47 | ? | -10 | -12 | ? |
Определите температуру по термометру в классе и на улице, как изменилась температура
| Температура | Вывод (как изменилась температура, на сколько?) |
| в классе (определить по термометру) | на улице (термометр на окне) |
| 21 24 | -3 -8 | ? ? |
2) Уровень моряПосмотрим на физическую карту мира. Участки суши на ней раскрашены различными оттенками зеленого и коричневого цветов, а моря и океаны раскрашены голубым и синим. Каждому цвету соответствует своя высота (для суши) или глубина (для морей и океанов). На карте нарисована шкала глубин и высот, которая показывает, какую высоту (глубину) означает тот или иной цвет
3) в жизни Баланс на телефоне Если у человека на телефоне отрицательный баланс, значит, он потратил денег больше, чем было у него на счету, то есть влез в долг. Когда человек в следующий раз пополнит баланс, сумма долга будет вычтена из положенных денег.
|
| Баланс телефона |
|
| ноябрь | декабрь | январь | февраль | март | баланс телефона |
| Арслан | 323 | -454 | 235 | -99 | 250 |
|
| Равзат | -159 | 207 | 367 | -236 | 400 |
|
| Рустам | -97 | 345 | -194 | 459 | 640 |
|
| Алтынай | -139 | 467 | -312 | -132 | 545 |
|
| решают |
| a | b | c | d | a-b+c-d |
| 1 ряд | 1 квартал | 15200 | -239 | -459 | 10973 |
|
| 2 ряд | 2 квартал | 4007 | 5820 | 209 | -11 |
|
| 3 ряд | 3 квартал | -1593 | -37403 | -40030 | -5080 |
|
| 4 ряд | 4 квартал | 860 | -10950 | 90000 | 1810 |
|
3)Мы еще говорили, что отрицательные числа встречаются в бизнесе. Задача : прибыль фирмы (в тыс. рублей) считается по формуле a-b+c-d, где значения a,b,c.d указаны в таблице: (каждая группа считает свою строчку) в данном квартале фирма имела прибыль или терпела убытки? Каковы их размеры?
ОТВЕТЫ
| 1 2 3 4 5 6
7 8 9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30 | - 3,4 + (- 1,8) – 3,2 + (- 4,8) -11,3 + 7,8 -37 + (- 5) - 4,8 + (- 3,5) -4,5 + (- 4,7)
-0,5 + (- 4,9) – 21,4 + 27,1 – 11,3 + 16,6 15 + (- 9,3) - 4,1 + 12,1 - 3,5 + (- 4,1)
1,6 + (- 1,6) – 9,6 + 3,5 16,3 + (- 8,3) – 4,9 + (- 2,9) – 9,2 + 9,2 4,6 + (- 10)
– 13,8 + 10,9 3,2 + (- 11,2) – 18 + 12,6 – 19,1 + 10,8 - 7,1 + 3,6 – 18,5 + 10,9
– 14,5 + 4,9 -13,7 + 8,3 37,1 + (-37,1) – 2,7 + (- 3,4) 15,1 + (- 5,8) 11,4 + (-17,5) | -5,2 -8 -3,5 -42 -8,3 -9,2
-5,4 5,7 5,3 5,7 8 -7,6
0 -6,1 8 -7,6 0 -5,4
-2,9 -8 -5,4 -8,3 -3,5 -7,6
-9,6 -5,4 0 -6,1 9,3 -6,1 | П О Д Р У Ж
И С Ь С М А
Т Е М А Т И
К О Й У Д А
Ч И Т Е Б Е |
Домашнее задание.
«Арифметика, сиречь наука числительная, с разных диалектов на славянский язык переведенная и во едино собрана, и на две книги разделена...» Так была названа громадная книга, написанная в 1709 г. одним из самых образованных людей России XVIII в. Она содержала не только сведения из арифметики, но и основы знаний по алгебре, геометрии, астрономии, метеорологии. Эту книгу можно назвать энциклопедией математических знаний того времени. Автор этой книги родился в 1669 г., а умер в 1739 г. Кто был автором первого русского учебника арифметики?
1)Ломоносов;
2)Радищев;
3)Магницкий.
Вы узнаете его имя, если выполните следующее задание:
а) Решите приведённые ниже примеры;
б) Выберете максимальный и минимальный результаты;
в) От модуля минимального результата отнимите максимальный результат;
г) Возьмите только целую часть и отнимите от неё число 3- полученное число и будет являться ответом.
а)-0,47 - 0,75 ;
б)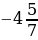 + (-1
+ (-1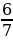 );
);
в) –0,36-0,83;
г)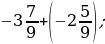
д)-5,2+ 4,7;
е) 0,55 + (-0,84);
ж) 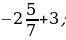
з) 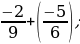
и) 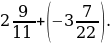 ;
;
к) 2,56+(- 3,13);
л)-4+2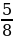
Ответ: 3 (Магницкий) вместо * цифры чтобы было верное равенство
| 1 вариант | 2 вариант |
| 1) -3 + * = -8 | 1) * + (-12) = -17 |
| 2) * + 5 = -10 | 2) -18 + * = -9 |
| 3) 25,3 + * = 19,1 | 3) * + (-8,4) = 15,2 |
| *⋅(-5)=-175 | 4) 42 ⋅ * = -168 |
| 5) -21 : * = 7 | 5) -35 : * = 5 |
| 6) * -6,8 = -4,5 | 6) 4,3 — *= -5,5 |








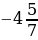 + (-1
+ (-1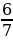 );
); 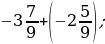
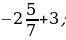
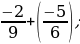
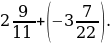 ;
;