ФГБОУ ВПО «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМЕНИ. М Е. ЕВСЕВЬЕВА»
Физико – математический факультет
Кафедра информатики и вычислительной техники
КУРСОВАЯ РАБОТА
ПРОБЛЕМЫ КОДИРОВАНИЯ ИНФОРМАЦИИ
Автор курсовой работы___________________________________ Д.А. Храмов
Направление подготовки 050100.62 Педагогическое образование
Профиль Математика. Информатика.
Руководитель работы
д.ф.–м.н., проф. каф. ИВТ______________________________ Е.В. Щенникова
Саранск 2013
Содержание
Введение…………………………………………………………………………...3
1 Кодирование информации……………………………………………………...5
1.1 Кодирование текстовой информации…………………………………5
1.2 Кодирование графической информации……………………….……..6
1.3 Кодирование звуковой информации………………………………….9
2 Шум и защита от шума. Теория кодирования К.Шеннона …………………11
3 Способы обнаружения ошибок с их последующим исправлением………...13
4 Основные понятия корректирующих кодов…………………………………15
4.1 Линейные и групповые коды………………………………………...17
4.2 Код Хэмминга………………………………………………………....21
Заключение……………………………………………………………………… 27
Список литературы………………………………………………………………28
Введение
Кодирование – процесс представления информации в виде кода. Под термином "кодирование", как правило, понимают переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки. Кодирование в узком смысле – способ сделать сообщение непонятным для всех, кто не владеет ключом кода.
Первым, кто использовал кодирование двух символьной информации, был Готфрид Вильгельм Лейбниц. Он считал: «Вычисление с помощью двоек … является для науки основным и порождает новые открытия. При сведении чисел к простым началам, каковыми являются 0 и 1, везде появляется чудесный порядок». Но, к сожалению, эта система была забыта.
Первым теоретическое решение проблемы передачи данных по зашумленным каналам предложил
Клод Шеннон, основоположник статистической теории информации. Работая в Bell Labs, Шеннон написал работу «Математическая теория передачи сообщений» (1948), где показал, что если пропускная способность канала выше энтропии источника сообщений, то сообщение можно закодировать так, что оно будет передано без излишних задержек.
Переход от теории к практике стал возможен благодаря усилиям Ричарда Хэмминга, коллеги Шеннона по Bell Labs, получившего известность за открытие класса кодов «коды Хэмминга».
Хэмминг первым предложил «коды с исправлением ошибок» (Error-Correcting Code, ECC). Современные модификации этих кодов используются во всех системах хранения данных и для обмена между процессором и оперативной памятью. Один из их вариантов, коды Рида-Соломона применяются в компакт-дисках, позволяя воспроизводить записи без скрипов и шумов, вызванных царапинами и пылинками. Существует множество версий кодов, построенных «по мотивам» Хэмминга, они различаются алгоритмами кодирования и количеством проверочных битов. Особое значение подобные коды приобрели в связи с развитием дальней космической связи с межпланетными станциями.
Цель моей курсовой работы, является ознакомление с методами обнаружения ошибок и защиты информации с помощью корректирующих кодов. Эта проблема в настоящее время относится к числу наиболее актуальных проблем, т.к. при обработке, передачи и хранении информации мы стремимся к повышению ее надежности.
Объект: процесс кодирования информации.
Задачи:
Проанализировать пособия по теории информации и информационной безопасности.
Выявить формы представления кодирования информации.
Обнаружение ошибок (проблем).
Методы и способы исправления ошибок.
1 Кодирование информации
Современный ПК может обрабатывать различную информацию (числовую, текстовую, звуковую и видео). Вся информация в компьютере представлена в двоичном коде, т.е. Используется алфавит мощностью два. Это связанно, прежде всего, с тем, что удобно представлять в виде последовательности электрических импульсов (импульс отсутствует — 0, импульс есть — 1). Логическая последовательность нулей и единиц называется, машинным кодом.
1.1 Кодирование текстовой информации
В настоящее время большая часть пользователей при помощи компьютера обрабатывает текстовую информацию, которая состоит из символов: букв, цифр, знаков препинания и др.
Традиционно для того чтобы закодировать один символ используют количество информации равное 1 байту, т. е. I = 1 байт = 8 бит. При помощи формулы, которая связывает между собой количество возможных событий К и количество информации I, можно вычислить сколько различных символов можно закодировать (считая, что символы - это возможные события): К = 2I 28 = 256, т.е. для представления текстовой информации можно использовать алфавит мощностью 256 символов.
Суть кодирования заключается в том, что каждому символу ставят в соответствие двоичный код от 00000000 до 11111111 или соответствующий ему десятичный код от 0 до 255.
Необходимо помнить, что в настоящее время для кодировки русских букв используют пять различных кодовых таблиц (КОИ - 8, СР1251, СР866, Мас, ISO), причем тексты, закодированные, при помощи одной таблицы не будут правильно отображаться в другой кодировке.
В большинстве случаев о перекодировке текстовых документов заботится пользователь, а специальные программы - конвертеры, которые встроены в приложения.
Начиная с 1997г. последние версии Microsoft Windows Office поддерживают новую кодировку Unicode, которая на каждый символ отводит по 2 байта, а поэтому, можно закодировать не 256 символов, а 65536 различных символов.
1.2 Кодирование графической информации
В середине 50-х годов для больших ЭВМ, которые применялись в научных и военных исследованиях, впервые в графическом виде было реализовано представление данных. В настоящее время широко используются технологии обработки графической информации с помощью ПК.
Особенно интенсивно технология обработки графической информации с помощью компьютера стала развиваться в 80-х годах. Графическую информацию можно представлять в двух формах: аналоговой или дискретной. Живописное полотно, цвет которого изменяется непрерывно - это пример аналогового представления, а изображение, напечатанное при помощи струйного принтера и состоящее из отдельных точек разного цвета - это дискретное представление. Чем большее количество цветов используется (т. е. точка изображения может принимать больше возможных состояний), тем больше информации несет каждая точка, а, значит, увеличивается качество кодирования. Создание и хранение графических объектов возможно в нескольких видах - в виде векторного, фрактального или растрового изображения.
Отдельным предметом считается 3D (трехмерная) графика, в которой сочетаются векторный и растровый способы формирования изображений.
Если говорить о кодировании цветных графических изображений, то нужно рассмотреть принцип декомпозиции произвольного цвета на основные составляющие. Применяют несколько систем кодирования: HSB, RGB и CMYK.
1) Модель HSB характеризуется тремя компонентами: оттенок цвета (Hue), насыщенность цвета (Saturation) и яркость цвета (Brightness). Можно получить большое количество произвольных цветов, регулируя эти компоненты.
2) Принцип метода RGB заключается в следующем: известно, что любой цвет можно представить в виде комбинации трех цветов: красного (Red, R), зеленого (Green, G), синего (Blue, B). Другие цвета и их оттенки получаются за счет наличия или отсутствия этих составляющих.
3) Принцип метода CMYK. Эта цветовая модель используется при подготовке публикаций к печати. Каждому из основных цветов ставится в соответствие дополнительный цвет (дополняющий основной до белого).
Различают несколько режимов представления цветной графики:
1) полноцветный (TrueColor);
2) HighColor;
3) индексный.
При полноцветном режиме для кодирования яркости каждой из составляющих используют по 256 значений (восемь двоичных разрядов), то есть на кодирование цвета одного пикселя (в системе RGB) надо затратить 8*3=24 разряда. Это позволяет однозначно определять 16,5 млн цветов. Это довольно близко к чувствительности человеческого глаза. При кодировании с помощью системы CMYK для представления цветной графики надо иметь 8*4=32 двоичных разрядов.
Режим HighColor - это кодирование при помощи 16-разрядных двоичных чисел, то есть уменьшается количество двоичных разрядов при кодировании каждой точки. Но при этом значительно уменьшается диапазон кодируемых цветов.
При индексном кодировании цвета можно передать всего лишь 256 цветовых оттенков. Каждый цвет кодируется при помощи восьми бит данных. Но так как 256 значений не передают весь диапазон цветов, доступный человеческому глазу, то подразумевается, что к графическим данным прилагается палитра (справочная таблица), без которой воспроизведение будет неадекватным: море может получиться красным, а листья - синими. Сам код точки растра в данном случае означает не сам по себе цвет, а только его номер (индекс) в палитре. Отсюда и название режима - индексный.
Соответствие между количеством отображаемых цветов (К) и количеством бит для их кодировки (а) находиться по формуле: К = 2а («Таблица 1») .
«Таблица 1»
| А | К | Достаточно для |
| 4 | 24 = 16 |
|
| 8 | 28 = 256 | Рисованных изображений типа тех, что видим в мультфильмах, но недостаточно для изображений живой природы |
| 16 (HighColor) | 216 = 65536 | Изображений, которые на картинках в журналах и на фотографиях |
| 24 (TrueColor) | 224 = 16 777 216 | Обработки и передачи изображений, не уступающих по качеству наблюдаемым в живой природе |
1.3 Кодирование звуковой информации
С начала 90-х годов персональные компьютеры получили возможность работать со звуковой информацией. Каждый компьютер, имеющий звуковую плату, микрофон и колонки, может записывать, сохранять и воспроизводить звуковую информацию. Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой. Чем больше амплитуда, тем он громче для человека, чем больше частота сигнала, тем выше тон. Программное обеспечение компьютера в настоящее время позволяет непрерывный звуковой сигнал преобразовывать в последовательность электрических импульсов, которые можно представить в двоичной форме.
Процесс преобразования звуковых волн в двоичный код в памяти компьютера:
Звуковая волна →Микрофон → Переменный электрический ток → Аудиоадаптер →Двоичный код → Память компьютера
Процесс воспроизведения звуковой информации, сохраненной в памяти компьютера:
Память компьютера → Двоичный код → Аудиоадаптер → Переменный электрический ток → Динамик → Звуковая волна
Аудиоадаптер (звуковая плата)– специальное устройство, подключаемое к компьютеру, предназначенное для преобразования электрических колебаний звуковой частоты в числовой двоичный код при вводе звука и для обратного преобразования (из числового кода в электрические колебания) при воспроизведении звука.
В процессе записи звука аудиоадаптер с определенным периодом измеряет амплитуду электрического тока и заносит в регистр двоичный код полученной величины.
Затем полученный код из регистра переписывается в оперативную память компьютера.
Качество компьютерного звука определяется характеристиками аудиоадаптера: частотой дискретизации и разрядностью.
Частота дискретизации – это количество измерений входного сигнала за 1 секунду.
Разрядность регистра– число бит в регистре аудиоадаптера.
2 Шум и защита от шума. Теория кодирования К.Шеннона
Термином «шум» называют разного рода помехи, искажающие передаваемый сигнал и приводящие к потере информации. Такие помехи возникают по техническим причинам: плохое качество линии связи, незащищенность друг от друга различных потоков информации, передаваемых по одним и тем же каналам. Например, при беседе по телефону, мы слышим шум и треск. В таких случаях необходима защита от шума. Способы защиты бывают самыми разными. Использование экранированного кабеля вместо «голого» провода; применение различных фильтров, отделяющих полезный сигнал от шума и т.п.
Клодом Шенноном была разработана специальная теория кодирования, дающая методы борьбы с шумом. Одна из важных идей этой теории состоит в том, что передаваемый по линии связи код должен быть избыточным. За счет этого потеря какой-то части информации при передаче может быть компенсирована. Например, если при разговоре по телефону вас плохо слышно, то, повторяя каждое слово дважды, вы имеете больше шансов на то, что собеседник поймет вас правильно.
Однако нельзя делать избыточность слишком большой. Это приведет к задержкам и удорожанию связи. Теория кодирования К. Шеннона как раз и позволяет получить такой код, который будет оптимальным. При этом избыточность передаваемой информации будет минимально возможной, а достоверность принятой информации — максимальной.
В современных системах цифровой связи часто применяется следующий прием борьбы с потерей информации. Все сообщение разбивается на порции — пакеты. Для каждого пакета вычисляется контрольная сумма (сумма двоичных цифр), которая передается вместе с данным пакетом. В месте приема заново вычисляется контрольная сумма принятого пакета, и если она не совпадает с первоначальной, то передача данного пакета повторяется. Так происходит пока исходная и конечная контрольные суммы не совпадут.
3 Способы обнаружения ошибок с их последующим исправлением
Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях сетевой модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
обнаружение ошибок в блоках данных и автоматический запрос повторной передачи поврежденных блоков — этот подход применяется, в основном, на канальном и транспортном уровнях;
обнаружение ошибок в блоках данных и отбрасывание поврежденных блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
Исправление ошибок применяется на физическом уровне.
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникших при передаче информации под влиянием помех, а так же при её хранении.
При записи в данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении её используют для того, чтобы обнаружить или исправить ошибки. Число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
Коды обнаружения ошибок в отличии от кодов исправляющих ошибки, могут только установить факт наличия ошибки.
Фактически любой код, исправляющий ошибки, может быть использован для их обнаружения. При этом он будет способен обнаружить большее число ошибок.
4 Основные понятия корректирующих кодов
Среди корректирующих кодов широко используются циклические коды, в ЭВМ эти коды применяются при последовательной передаче данных между ЭВМ и внешними устройствами, а также при передаче данных по каналам связи. Для исправления двух и более ошибок (d0 5) используются циклические коды БЧХ (Боуза - Чоудхури - Хоквингема), а также Рида-Соломона, которые широко используются в устройствах цифровой записи звука на магнитную ленту или оптические компакт-диски и позволяющие осуществлять коррекцию групповых ошибок. Способность кода обнаруживать и исправлять ошибки достигается за счет введений избыточности в кодовые комбинации, т.е. кодовым комбинациям из к двоичных информационных символов, поступающих на вход кодирующего устройства, соответствует на выходе последовательность из n двоичных символов (такой код называется (n, k) - кодом).
Если N0 = 2n-общее число кодовых комбинаций, а N = 2k - число разрешенных, то число запрещенных кодовых комбинаций равно
N0-N = 2n -2k.
При этом число ошибок, которое приводит к запрещенной кодовой комбинации равно (1).
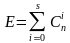 (1)
(1)
где S - кратность ошибки, т.е. количество искаженных символов в кодовой комбинации S = 0, 1, 2, …
Cni- сочетания из n элементов по i, вычисляемое, по формуле (2)
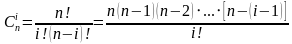 (2)
(2)
для S = 0; 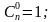
S = 1; 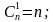
S = 2; 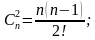
S= 3; 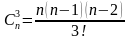 и т.д.
и т.д.
Для исправления S ошибок количество комбинаций кодового слова, составленного из m проверочных разрядов N = 2m, должно быть больше возможного числа ошибок (3), при этом количество обнаруживаемых ошибок в два раза больше, чем исправляемых
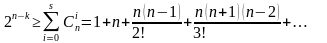 (3)
(3)
2m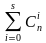 откуда
откуда 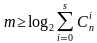 .
.
Для одиночной ошибки, как наиболее вероятной 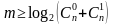 .
.
В зависимости от исходных данных кода (n или k) можно использовать
формулы (4).
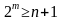 или
или 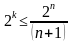 (4)
(4)
При этом, m = [log2(1+n)] или m = [log2 {(k+1)+ [log2(k+1)]}], где квадратные скобки обозначают округление до большего целого.
В таблице приведены соотношения между длиной кодовой комбинации и количеством информационных и контрольных разрядов для кода исправляющего одиночную ошибку, а также эффективность использования канала связи.
Для исправления двукратной ошибки (5).
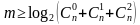 или
или 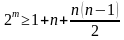 (5)
(5)
Введение избыточности в кодовые комбинации при использовании корректирующих кодов существенно снижает скорость передачи информации и эффективность использования канала связи.
Например, для кода (31, 26) скорость передачи информации равна
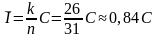 («Таблица 2»), т.е. скорость передачи уменьшается на 16%.
(«Таблица 2»), т.е. скорость передачи уменьшается на 16%.
«Таблица 2»
| n | 7 | 10 | 15 | 31 | 63 | 127 | 255 |
| k | 4 | 6 | 11 | 26 | 57 | 120 | 247 |
| m | 3 | 4 | 4 | 5 | 6 | 7 | 8 |
| 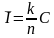
| 0,57 | 0,6 | 0,75 | 0,84 | 0,9 | 0,95 | 0,97 |
Как видно из таблицы , чем больше n, тем эффективнее используется канал.
4.1 Линейные и групповые коды
Линейным называется код, в котором проверочные символы представляют собой линейные комбинации информационных.
Групповым называется код, который образует алгебраическую группу по отношению операции сложения по модулю два.
Свойство линейного кода: сумма (разность) кодовых векторов линейного кода дает вектор, принадлежащий этому коду.
Свойство группового кода: минимальное кодовое расстояние между кодовыми векторами равно минимальному весу ненулевых векторов. Вес кодового вектора равен числу единиц в кодовой комбинации.
Групповые коды удобно задавать при помощи матриц, размерность которых определяется параметрами k и n. Число строк равно k, а число столбцов равно n = k+m.(6).
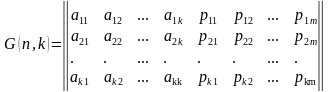 . (6)
. (6)
Коды, порождаемые этими матрицами, называются (n, k)-кодами, а соответствующие им матрицы порождающими (образующими, производящими). Порождающая матрица G состоит из информационной Ikk и проверочной Rkm матриц. Она является сжатым описанием линейного кода и может быть представлена в канонической (типовой) форме (7).
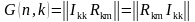 (7)
(7)
В качестве информационной матрицы удобно использовать единичную матрицу, ранг которой определяется количеством информационных разрядов (8).
 (8)
(8)
Строки единичной матрицы представляют собой линейно-независимые комбинации (базисные вектора), т.е. их по парное суммирование по модулю два не приводит к нулевой строке.
Строки порождающей матрицы представляют собой первые k комбинаций корректирующего кода, а остальные кодовые комбинации могут быть получены в результате суммирования по модулю два всевозможных сочетаний этих строк.
Столбцы добавочной матрицы Rkm определяют правила формирования проверок. Число единиц в каждой строке добавочной матрицы должно удовлетворять условию r1 d0-1, но число единиц определяет число сумматоров по модулю 2 в шифраторе и дешифраторе, и чем их больше, тем сложнее аппаратура.
Производящая матрица кода G(7,4) может иметь вид
 и т.д.
и т.д.
Процесс кодирования состоит во взаимно - однозначном соответствии к-разрядных информационных слов - I и n-разрядных кодовых слов – с(9)
c=IG (9)
Например: информационному слову I=[1 0 1 0] соответствует кодовое слово (10).
 (10)
(10)
При этом, информационная часть остается без изменений, а корректирующие разряды определяются путем суммирования по модулю два тех строк проверочной матрицы, номера которых совпадают с номерами разрядов, содержащих единицу в информационной части кода.
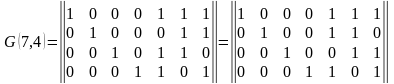
Процесс декодирования состоит в определении соответствия принятого кодового слова, переданному информационному. Это осуществляется с помощью проверочной матрицы H(n, k) (11).
 (11)
(11)
где RmkT -транспонированная проверочная матрица (поменять строки на столбцы); Imm- единичная матрица.
Для (7, 4)- кода проверочная матрица имеет вид (12).
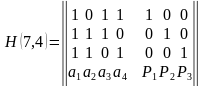 (12)
(12)
Между G(n ,k) и H(n, k) существует однозначная связь, т.к. они определяются в соответствии с правилами проверки, при этом для любого кодового слова должно выполняться равенство cHT= 0.
Строки проверочной матрицы определяют правила формирования проверок. Для (7, 4)-кода соответствует (13).
p1+a1+a2a4 = S1 ;
p2+a1+a2a3 = S2 ; (13)
p3+a1+a3a4 = S3 .
Полученный синдром сравниваем со столбцами матрицы и определяем разряд, в котором произошла ошибка, номер столбца равен номеру ошибочного разряда. Для исправления ошибки ошибочный бит необходимо проинвертировать.
4.2 Код Хемминга
Код Хэмминга относится к классу линейных кодов и представляет собой систематический код – код, в котором информационные и контрольные биты, расположены на строго определенных местах в кодовой комбинации.
Код Хэмминга, как и любой (n, k)- код, содержит к информационных и m = n-k избыточных (проверочных) бит.
Избыточная часть кода строится т.о. чтобы можно было при декодировании не только установить наличие ошибки но, и указать номер позиции, в которой произошла ошибка, а значит, и исправить ее, инвертировав значение соответствующего бита.
Существуют различные методы реализации кода Хэмминга и кодов которые являются модификацией кода Хэмминга. Рассмотрим алгоритм построения кода для исправления одиночной ошибки.
По заданному количеству информационных символов - k, либо информационных комбинаций N = 2k , используя соотношения (14).
n = k+m, 2n (n+1)2k и 2m n+1 (14)
m = [log2 {(k+1)+ [log2(k+1)]}]
вычисляют основные параметры кода n и m.
2. Определяем рабочие и контрольные позиции кодовой комбинации. Номера контрольных позиций определяются по закону 2i,где i=1, 2, 3,... т.е. они равны 1, 2, 4, 8, 16,… а остальные позиции являются рабочими.
3. Определяем значения контрольных разрядов (0 или 1 ) при помощи многократных проверок кодовой комбинации на четность. Количество проверок равно m = n-k. В каждую проверку включается один контрольный и определенные проверочные биты. Если результат проверки дает четное число, то контрольному биту присваивается значение - 0, в противном случае - 1. Номера информационных бит, включаемых в каждую проверку, определяются по двоичному коду натуральных n –чисел разрядностью – m или при помощи проверочной матрицы H(mn), столбцы которой представляют запись в двоичной системе всех целых чисел от 1 до (2k –1) перечисленных в возрастающем порядке. Для m = 3 проверочная матрица имеет вид (15).
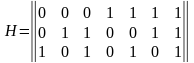 (15 )
(15 )
Количество разрядов m - определяет количество проверок («Таблица 3»).
В первую проверку включают коэффициенты, содержащие 1 в младшем (первом) разряде, т.е. b1, b3, b5 и т.д.
Во вторую проверку включают коэффициенты, содержащие 1 во втором разряде, т.е. b2, b3, b6 и т.д.
В третью проверку - коэффициенты которые содержат 1 в третьем разряде и т.д.
«Таблица 3»
| Десятичные числа (номера разрядов кодовой комбинации) | Двоичные числа и их разряды
|
| 3 | 2 | 1 |
| 1 2 3 4 5 6 7 | 0 0 0 1 1 1 1 | 0 1 1 0 0 1 1 | 1 0 1 0 1 0 1 |
Для обнаружения и исправления ошибки составляются аналогичные проверки на четность контрольных сумм, результатом которых является двоичное (n-k) -разрядное число, называемое синдромом и указывающим на положение ошибки, т.е. номер ошибочной позиции, который определяется по двоичной записи числа, либо по проверочной матрице.
Для исправления ошибки необходимо проинвертировать бит в ошибочной позиции. Для исправления одиночной ошибки и обнаружения двойной используют дополнительную проверку на четность. Если при исправлении ошибки контроль на четность фиксирует ошибку, то значит в кодовой комбинации две ошибки.
В ЭВМ код Хэмминга чаще всего используется для обнаружения и исправления ошибок в ОП, памяти с обнаружением и исправлением ошибок ECCMemory (ErrorCheckingandCorrecting). Код Хэмминга используется как при параллельной, так и при последовательной записи. В ЭВМ значительная часть интенсивности потока ошибок приходится на ОП. Причинами постоянных неисправностей являются отказы ИС, а случайных изменение содержимого ОП за счет флуктуации питающего напряжения, кратковременных помех и излучений. Неисправность может быть в одном бите, линии выборки разряда, слова либо всей ИС. Сбой может возникнуть при формировании кода (параллельного), адреса или данных, поэтому защищать необходимо и то и др. Обычно дешифратор адреса встроен в микро схему и недоступен для потребителя. Наиболее часто ошибки дают ячейки памяти ЗУ, поэтому главным образом защищают записываемые и считываемые данные.
Наибольшее применение в ЗУ нашли коды Хэмминга с dmin=4, исправляющие одиночные ошибки и обнаруживающие двойные.
Проверочные символы записываются либо в основное, либо специальное ЗУ. Для каждого записываемого информационного слова (а не байта, как при контроле по паритету) по определенным правилам вычисляется функция свертки, результат которой разрядностью в несколько бит также записывается в память. Для 16-ти разрядного информационного слова используется 6 дополнительных бит (32 - 7 бит, 64 – 8 бит). При считывании информации схема контроля («Рис. 1»), используя избыточные биты, позволяет обнаружить ошибки различной кратности или исправить одиночную ошибку. Возможны различные варианты поведения системы:
автоматическое исправление ошибки без уведомления системы;
исправление однократной ошибки и уведомление системы только о многократных ошибках;
не исправление ошибки, а только уведомление системы об ошибках;
Модуль памяти со встроенной схемой исправления ошибок – EOS 72/64 (ECConSimm). Аналог микросхема к 555 вж 1 -это 16 разрядная схема с обнаружением и исправлением ошибок (ОИО) по коду Хэмминга G(22, 16), использование которой позволяет исправить однократные ошибки и обнаружить все двух кратные ошибки в ЗУ.
Избыточные (контрольные) разряды позволяют обнаружить и исправить ошибки в ЗУ в процессе записи и хранения информации.
В составе ВЖ-1 используются 16 информационных и 6 контрольных разрядов. (DB - информационное слово, CB - контрольное слово).
При записи осуществляется формирование кода, состоящего из 16 информационных и 6 контрольных разрядов, представляющих результат суммирование по модулю 2 восьми информационных разрядов в соответствии с кодом Хэмминга. Сформированные контрольные разряды вместе с информационными поступают на схему и записываются в ЗУ.
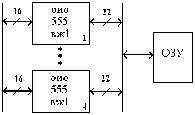
«Рис. 1» - схема контроля
При считывании шестнадцатиразрядное слово декодируется, восстанавливаясь вместе с 6 разрядным словом контрольным, поступают на схему сравнения и контроля. Если достигнуто равенство всех контрольных разрядов и двоичных слов, то ошибки нет.
Любая однократная ошибка в 16 разрядном слове данных изменяет 3 байта в 6 разрядном контрольном слове. Обнаруженный ошибочный бит инвертируется.
Заключение
Цель моей работы достигнута: я познакомился с методами обнаружения ошибок и защиты информации с помощью корректирующих кодов. Рассмотрел циклические коды, исправляющие более 2 ошибок (к ним относятся коды БЧХ (Боуза - Чоудхури - Хоквингема) и Рида-Соломона) и линейные коды (коды Хемминга). Все они основываются на избыточности информации.
Научились находить эту избыточность с помощью формул. Узнал, что любой код, исправляющий ошибки, может быть использован для их обнаружения. При этом он будет способен обнаружить большее число ошибок.
Познакомился с различными способами кодирования различных видов информации: текстовой, графической и звуковой.
Список литературы
Недвоичные арифметические корректирующие коды, проблемы передачи информации / В.М. Гриценко — 4-е изд. – 1969. – 19 – 27 с.
Помехоустойчивые коды в системах связи / Б.М. Золотник — M.: Радио и связь, 1989.—232 c.
Информационная безопасность. Лабораторный практикум: учебное пособие / А.В. Бабаш, Е.К. Баранова, Ю.Н. Мельникова. — М.: КНОРУС, 2012. – 136 с.
Теория передачи сигналов / Кловский Д.Д. — M.: Cвязь, 1984.
Цифровое кодирование звуковых сигналов / Ковалгин Ю.A., Вологдин Э.И. — Изд-во Kорона-принт, 2004. – 240с.
Курс теории информации / Колесников B.Д., Полтырев Г.Ш. — M.: Наука, 1982. 416 с.
Микропроцессорные кодеры и декодеры / В.М. Муттер, Г.A. Петров и др.—M.: Радио и связь, 1991.—184 с.
Экономное кодирование дискретной информации / Семенюк В. В. – СПб: СПбГИТМО (ТУ), 2001. – 115 с.







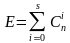 (1)
(1)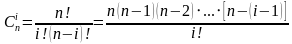 (2)
(2)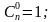
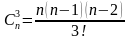 и т.д.
и т.д. 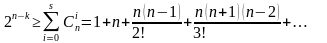 (3)
(3) откуда
откуда 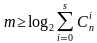 .
.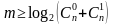 .
.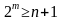 или
или 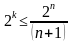 (4)
(4)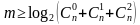 или
или 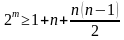 (5)
(5)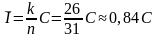 («Таблица 2»), т.е. скорость передачи уменьшается на 16%.
(«Таблица 2»), т.е. скорость передачи уменьшается на 16%.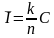
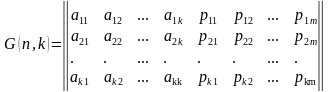 . (6)
. (6)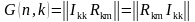 (7)
(7) (8)
(8) и т.д.
и т.д. (10)
(10)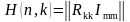 (11)
(11)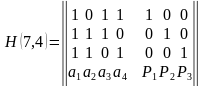 (12)
(12)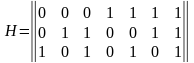 (15 )
(15 )










