Квадраттык тендемени тушундуруу

САБАКТЫН МАКСАТЫ:

1.Кадраттык тендеме жана толук эмес квадраттык тендеме жөнүндө маалымат аласынар.Толук квадраттык тендеменин коэффициентерин аныктаганды жана толук эмес квадраттык тендемелердин чыгарыылышын үйрөнөсүнөр.

КВАДРАТТЫК ТЕНДЕМЕНИН АНЫКТАМАСЫ.

ах 2 + bx + c =0 ,

Т үрүндөгү тендеме квадраттык тендеме деп аталат.

а≠0

х – өзгөрмө;

а, b жана с – ар кандай анык сандар,

а – биринчи коэффициент

b – экинчи коэффициент

с – бош мүчө

КВАДРАТТЫК ТЕНДЕМЕГЕ МИСАЛ КАРАП КӨРӨЛҮ

ТӨМӨНКҮЛӨР КВАДРАТТЫК ТЕНДЕМЕ БОЛОБУ?

а) 3,7х 2 -5х+1=0

б) 48х 2 –х 3 -9=0

в) 2,1х 2 +2х-0,11=0

г) 1-12х=0

Квадраттык тендеменин коэффициенттерин аныктап тетрадтарга жазгыл

а) 6х 2 – х + 4 = 0

б) 12х - х 2 + 7 = 0

в) 8 + 5х 2 = 0

г) х – 6х 2 = 0

д) - х + х 2 = 15

а = 6, в = -1, с = 4;

а = -1, в = 12, с = 7;

а = 5, в = 0, с = 8;

а = -6, в =1, с = 0;

а = 1, в =-1, с = -15.

Квадраттык тендеме т үзгүлө , эгер:

а) а = 5, b = -3, с = 8

б ) b = 2, с = -6, а = - 4

5х 2 – 3х + 8 = 0

– 4х 2 + 2 х – 6 = 0

КВАДРАТТЫК ТЕНДЕМЕ

ТОЛУК КВАДРАТТЫК ТЕНДЕМЕ

ТОЛУК ЭМЕС КВАДРАТТЫК ТЕНДЕМЕ

а ≠ 0, в ≠ 0, с ≠ 0

а ≠ 0, в = 0, с = 0

2х 2 +5х-7=0

6х+х 2 -3=0

Х 2 -8х-7=0

25-10х+х 2 =0

3х 2 -2х=0

2х+х 2 =0

125+5х 2 =0

49х 2 -81=0

Толук эмес квадраттык тендеме:

b  0

c = 0

2

а  0

х

b

0

а

х

=

+

2

х

c  0

b = 0

а  0

а

0

c

+

=

2

х

а

c = 0

0

b = 0

а  0

=

Кобойтүүчүлөргө

ажыратабыз

Төмөнкү түргө келтиребиз

жана

1-жолу: эгерде

Бир

Тамырга

ээ

- саны терс сан болсо, анда тамырга ээ эмес

2 -жолу: эгерде

- саны он сан болсо , анда эки тамырга ээ

ТӨМӨНКҮЛӨРДӨН ТОЛУК ЭМЕС КВАДРАТТЫК ТЕНДЕМЕЛЕРДИ БӨЛҮП ЖАЗГЫЛА.

Толук эмес квадраттык тендеме

• Толук эмес квадраттык тендемелердин чыгарылышын карап көрөлү.

1 . AX 2 +С =0 , С≠0

- 3х 2 +15=0

• Бош мүчөнү барабардыктын сол жагына алып өтөбүз.
• Барабардыктын эки жагын тен -3кө бөлөбүз.

-3х 2 =-15,

х 2 =5.

жообу:

2. АХ 2 + B Х=0, B≠0

5х 2 +7х=0

Тендеменин сол жагын көбөйтүүчүлөргө ажыратабыз:

х(5х+7)=0

х=0 жана 5х+7=0

5х=-7

х=

Жообу : - 1,4; 0

х(2х – 5)=0;

х=0 жана 2х-5=0;

х=0 жана х=2,5.

Жообу: 0; 2,5.

3у(1 – 6у)=0;

3у=0 ж-а1-6у=0;

у=0 жана у = .

Жообу: 0;

16

3 . AX 2 =0 , ГДЕ А≠0

3,8 x 2 =0

Барабардыктын эки жагын тен 3,8ке бөлөбүз:

x 2 = 0

Жообу : 0.

Төмөнкү тендемелер канча тамырга ээ болорун көрөлү

Эки

тамырга э э

7х ² =0

14х ² +5х=0

3,6х ² +1=0

Х ² +3=0

4х ² +7=0

18-х ² =0

6х+х ² =0

2х ² +3=0

Бир

тамырга ээ

Тамырга ээ эмес

ТОЛУК ЭМЕС КВАДРАТТЫК ТЕНДЕМЕНИ ЧЫГАРГЫЛА.

• 2 x 2 = 0
• 4 x 2 – 64 = 0
• x 2 -7х = 0
• 25 – 16 x 2 = 0
• 5 x 2 = 3х

• 2 x 2 = 18
• 0,01 x 2 = 4
• х - 2 x 2 = 0
• 4 x 2 + 12 = 0
• 12 x 2 + 3х = 0

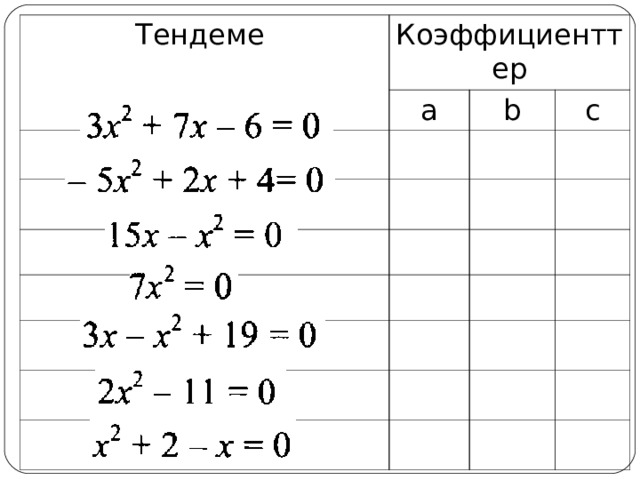
Тендеме

Коэффициенттер

a

b

c

ТЕНДЕМЕНИН КОЭФФИЦИЕНТТЕРИН АТАГЫЛА

а б с

8 0 1

7 1 0

9 1 4

коэффициенттерди пайдаланып квадраттык тендеме түзгүлө:

a

1

2

b

-5

c

1

3

4

1

4

Тендеме

0

-7

-16

4

3

5

-2

0

-1

-5

0

4

Тапшырма :

а

- 2

в

3

1

с

- 5

2

4

7

0

0

6

- 8

0

0

- 3

1

-2 х² + 3х - 5= 0

x² + 4х = 0

2 х² - 8 = 0

7 x² = 0

6х ²- 3х + 1 = 0

Тапшырма

1 ) а = 3 b = -2 с = 1

2) а = 1 b = 2 c = 0

3) а = 3 b = 0 с = 4

4) а = -4 b = 0 с = 0

5) а = 9 b = 0 c = -4

6) а = 3 b = -4 c = 0