11 класс тема «Логарифм» Учитель: Рудая В.В.
ЛЕКЦИЯ 2 Свойства логарифма
Вспомним полученные знания из лекции 1 по данной теме и ответим на вопросы (устно):
1. Дайте определение логарифма числа.
2. Дайте определение десятичного логарифма.
3. Сформулируйте основное логарифмическое тождество
4. Перечислите изученные свойства логарифмов.
Вычислите (в тетрадях):
5 10. 2
10. 2 +
+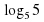
 11.
11. 
2 12.
12.  -
-
 13. 2
13. 2
 14.
14. 

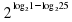
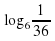
( )
)
Если возникли трудности, то вспомни свойства степеней и корней: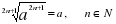
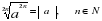
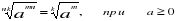

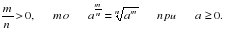




Введем новые свойства логарифмов, с помощью которых вы должны научиться решать и упрощать выражения, содержащие логарифмы
В тетради оформляем таблицу (переписываем и разбираемся по каждому свойству!)
| № | Название свойства логарифмов | Свойства логарифмов | Пример |
| 1. | Логарифм единицы. | log a1 = 0, a 0, a  1. 1. | log321 =0 |
| 2. | Логарифм основания. | log aa = 1, a 0, a  1. 1. | Log328 + Log324 |
|
| Логарифм произведения. | log a(xy) = log ax + logay, a 0, a  1, x 0, y 0. 1, x 0, y 0. | log328 + log324 = =log3232 =1 |
| 4. | Логарифм дроби. | log a  = log ax – logay, = log ax – logay, a 0, a ? 1, x 0, y 0. |
log3 54 - log32 = =log327 =3 |
| 5. | Логарифм степени. | log ax = =  log ax, log ax,
x 0, a 0, a  1, 1,   R. R. | log3 2767 = 67 log3 27 = 67*3 = 201
log3 (-27)8 = 8 log3 | -27| = 8*3 = 24 (под логарифмом не может быть отрицательного числа !!!)
|
| Замечание. | log ax2k = 2k log a |x| ,
a 0, a  1, k 1, k N , x N , x  R, R,
x  0. 0. |
| 6. | Логарифм выражения по основанию, которое является степенью. | log a x = x =  log ax, a 0, log ax, a 0,
a  1, x 0, 1, x 0,   R, R,   0 . 0 . | Этого свойства в учебнике нет, но оно важное!  =1/4 log2 2 = ¼ = 0,25 =1/4 log2 2 = ¼ = 0,25
(т.о, показатель основания «выходит» из логарифма обратным числом)
Лишний раз проверь при вынесения показателя – под логарифмом должно остаться положительное число!!!
 = 7/4 log2 2 = 7/4 =1,75 = 7/4 log2 2 = 7/4 =1,75
(если сразу использовать свойства 5 и 6) |
| Замечание: | 1. log a2kx =  log |a|x, log |a|x,
a  0, a 0, a   1, x 0, k 1, x 0, k  N. N.
2. log a x x  = =  logax, a 0, logax, a 0,
a  1, 1,   R, R,   R, R,   0 , x 0. 0 , x 0. |
| 7. | Переход к новому основанию. |  = =
a 0, a  1, c 0, c 1, c 0, c  1, b 0. 1, b 0. |  = = ; ;  = =
 = =  (это свойство используется когда основание надо поменять местами с подлогарифмируемым выражением) (это свойство используется когда основание надо поменять местами с подлогарифмируемым выражением)
|
| Замечание. | log ab =  , ,
a 0, a  1, b 0, b 1, b 0, b  1. 1. |
Вся теория логарифмов строится на определении и свойствах. Определение надо выучить, а свойства отработать на упражнениях. Приступим!
Из учебника в тетради выполнить задания №488, №489, №490, №495, 496.
У многих из вас возникает вопрос «А где же эти логарифмы встречаются и применяются в жизни?»
Историческая справка по теме.
«Зачем и где применяются логарифмы»
Знания логарифмов и основных логарифмических свойств необходимы для людей многих профессий: физиков, химиков, астрономов, психологов, географов и экологии.
Логарифмы по основанию 10 до изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки
Логарифмическая линейка хорошо знакома нашим родителям. Она позволяет выполнять умножение и деление чисел, возведение в степень и вычисление квадратных и кубических корней.
Шкала Рихтера - классификация силы землетрясений, созданная и представленная в 1935 г. геологом Чарльзом Рихтером. Шкала основана на принципе логарифма: каждое деление увеличивается в 10 раз, и его основанием является общая энергия, выделяемая при землетрясении.
В 1858 году немецкий физик и психолог Густав Фехнер доказал, основной психофизический закон, в котором говорится, что интенсивность воспринимаемого нами ощущения пропорциональна логарифму силы раздражения. Его формулируют так: «При изменении силы раздражителя в геометрической прогрессии, интенсивность ощущения меняется в арифметической прогрессии».
Логарифмы применяются и в психических явлениях. «Шкала Ландау» самый яркий пример. Знаменитый физик по ней оценивал заслуги своих коллег. Шкала была логарифмическая (классу 2 отвечали достижения в 10 раз меньше, чем для класса 1). Из физиков имел класс 0,5, Бор, Дирак, Гейзенберг имели класс 1
Астрономы измеряют «блеск» небесных светил в звездных величинах. Блеск в астрономии — величина пропорциональная логарифму светового потока. Её направление обратное: чем больше значение звездной величины, тем слабее блеск объекта.
Xимическая шкала кислотности очень близка к шкале звездных величин. Чем выше кислотность, тем ниже значение индекса, основанием логарифма служит число 10.
Играя на рояле, пианист играет на логарифмах. Ступени темперированной хроматической гаммы представляют логарифмы этих величин с основанием
Логарифмическая спираль часто встречается в природе. Впервые логарифмическая спираль описана Декартом, а потом была исследована Бернулли.
Паук Эпейра сплетая паутину, закручивает паутину, скручивая нити вокруг центра по логарифмической спирали.
Живые существа обычно растут во всех направлениях , сохраняя общее начертание своей формы. Раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину им приходится скручиваться.
Многие Галактики закручены по логарифмической спирали. Солнечная система, как одна из Галактик тоже закручена по такой спирали.
Предлагаю творческую работу - презентацию по данной теме (можно объединиться в творческую группу)
Вы сегодня погрузились в логарифмы,
Безошибочно их надо вычислять,
На экзамене, конечно, вы их встретите,
Остаётся вам успехов пожелать.
На следующем занятии продолжим изучать свойства логарифмов на более сложном уровне.
2





 10. 2
10. 2 +
+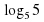
 11.
11. 
 12.
12.  -
-
 13. 2
13. 2 14.
14. 

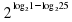
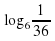
 )
)
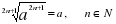
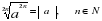
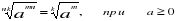

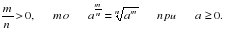




 =1/4
=1/4  = 7/4
= 7/4 









