Просмотр содержимого документа
«Лекция. Определители второго и третьего порядка. Разложение определителя по элементам строки или столбца.»
Элементы линейной алгебры.
Лекция 2. Определители второго и третьего порядков.
Разложение элементов определителя по элементам строки или столбца
Лекция 2. Определители второго и третьего порядка. Разложение определителя по элементам строки или столбца.
2.1 Определители второго и третьего порядка.
Пусть дана квадратная матрица второго порядка А = 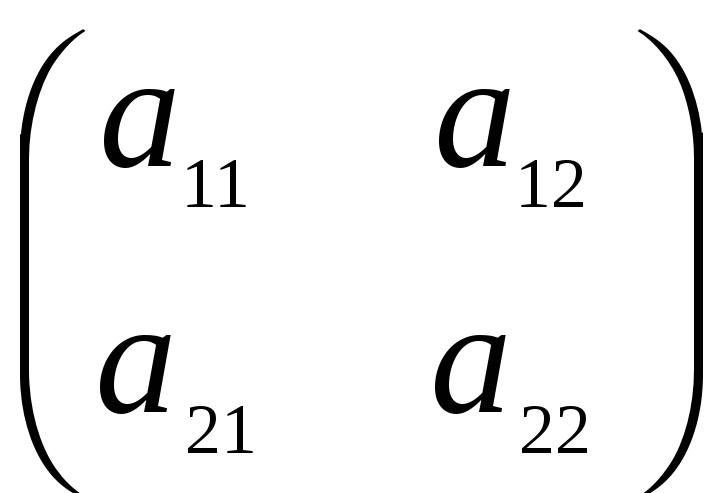
Определение 1. Определителем второго порядка, соответствующим данной матрице А, называется число, обозначаемое  и вычисляемое по формуле
и вычисляемое по формуле 
Пример 1
Вычислить определители второго порядка:
а) 
б) 
в) 
Пусть дана квадратная матрица третьего порядка А = 
Определение 2. Определителем третьего порядка, соответствующим данной матрице А, называется число, обозначаемое  и вычисляемое по формуле
и вычисляемое по формуле


При вычислении определителей третьего порядка удобно пользоваться правилом треугольников (или Саррюса), которое можно символически изобразить следующим образом:




![]()






«+» «–»
Пример 2
Вычислить определители третьего порядка:
а) =
=
б)
Свойства определителей
Величина определителя не изменится, если его строки и столбцы поменять местами.
При перстановке двух строк или двух столбцов определитель изменит свой знак на противоположный.
Если определитель имеет две одинаковые строки или два одинаковых столбца, то он равен нулю.
Общий множитель всех элементов строки или столбца можно вынести за знак определителя.
Если все элементы двух строк или двух столбцов пропорциональны, то определитель равен нулю.
Если к элементам какой – либо строки или столбца определителя прибавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число, то величина определителя не изменится.
Если все элементы какой – либо строки или столбца равны нулю, то и сам определитель равен нулю.
Миноры и алгебраические дополнения
Определение 3. Минором некоторого элемента определителя называется определитель, получаемый из данного вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.
Обозначение  , где i – номер строки, j – номер столбца, на пересечении которых расположен данный элемент.
, где i – номер строки, j – номер столбца, на пересечении которых расположен данный элемент.
Пример 3
Найти миноры и из определителя
Для нахождения минора вычеркиваем первую строку и второй столбик, оставшиеся числа выписываем в определитель второго порядка, получаем:
Для нахождения минора вычеркиваем третью строку и третий столбик, оставшиеся числа выписываем в определитель второго порядка, получаем:
Определение 4. Алгебраическим дополнением некоторого элемента определителя называется минор  этого элемента, умноженный на , где i – номер строки, j – номер столбца, на пересечении которых расположен данный элемент.
этого элемента, умноженный на , где i – номер строки, j – номер столбца, на пересечении которых расположен данный элемент.
Обозначение
Пример 4
Найти алгебраические дополнения для элементов а12 и а33 из определителя
Разложение определителя по элементам строки или столбца
Теорема. Определитель равен сумме произведений элементов какой – либо строки или столбца на их алгебраические дополнения.
А =
При вычислении определителя данным способом необходимо подчеркнуть строку или столбец, по элементам которой будем раскладывать определитель. Для упрощения вычислений лучше выбирать ту строчку или тот столбик, среди элементов которых есть нули.
Пример 5
Вычислить определитель, разложив его по элементам строки или столбца.
а )
)
б )
)
4






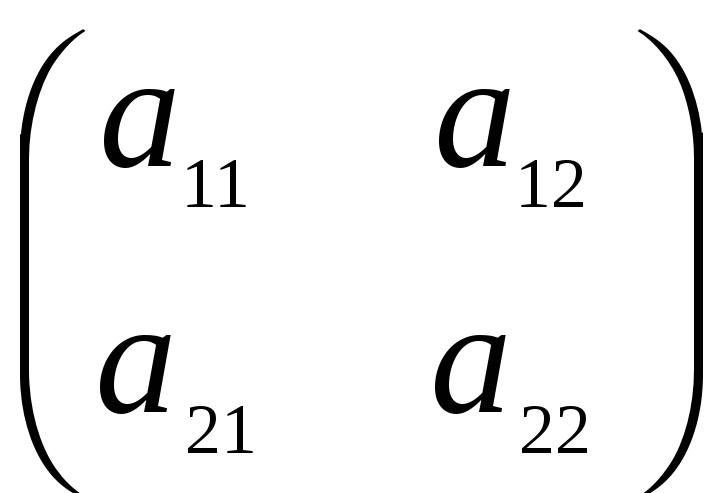

 и вычисляемое по формуле
и вычисляемое по формуле








 =
=










