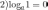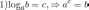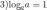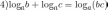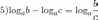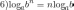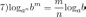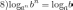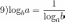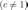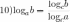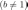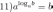Муниципальное бюджетное общеобразовательное учреждение
средняя школа №75
Логарифмы
“Логарифм числа  по основанию
по основанию  – показатель степени, в которую нужно возвести число
– показатель степени, в которую нужно возвести число  , чтобы получить число
, чтобы получить число  .”
.”
Выполнил
Ученик 11 класса “A”
Круглов Андрей
Руководитель: Малкова Елена Михайловна
г. Ульяновск, 2016
Цель проекта: обобщить знания о логарифмах.
Содержание:
• История появления логарифмов
• Применение логарифмов
• Логарифмические зависимости в науке и в природе
• Графики логарифмов и их свойства
• График натурального логарифма
• Основные свойства логарифмов
История появления логарифмов
Идейным источником и стимулом применения логарифмов послужил тот факт, что при перемножении степеней их показатели складываются: 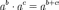 . Индийский математик VIII века Вирасена, исследуя степенные зависимости, опубликовал таблицу целочисленных показателей (то есть, фактически, логарифмов) для оснований 2, 3, 4.
. Индийский математик VIII века Вирасена, исследуя степенные зависимости, опубликовал таблицу целочисленных показателей (то есть, фактически, логарифмов) для оснований 2, 3, 4.
Джон Непер (1550-1617)
Михаэль Штифель
(1487-1567)
Решающий шаг был сделан в средневековой Европе. Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел, а также извлечением корней. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание, упростятся также возведение в степень и извлечение корня.


Первым эту идею опубликовал в своей книге «Arithmetica integra» (1544) , однако он не приложил серьёзных усилий для практической реализации своей идеи. Главной заслугой Штифеля является переход от целых показателей степени к произвольным рациональным.
В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов». В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1'. Термин логарифм, который был предложен Непером, утвердился в науке.
Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую. Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма.
Как вскоре обнаружилось, из-за ошибки в алгоритме все значения таблицы Непера содержали неверные цифры после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики. Немецкий математик и астроном Иоганн Кеплер в изданный им астрономический справочник 1620 года вставил восторженное посвящение Неперу (не зная, что изобретатель логарифмов уже скончался). В 1624 году Кеплер опубликовал свой собственный вариант логарифмических таблиц.
В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.
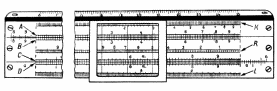
Логарифмическая линейка
Леонард Эйлер (1707-1783)
 Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.
Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.
Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.
Применение логарифмов
Логарифмы применяются для измерения энергетических (мощность, энергия) или силовых (напряжение, сила тока) величин. Эти величины встречаются практически во всех разделах физики.
В момент причаливания корабля к пристани, для того чтобы его остановить , используют следующий прием. С судна на пристань бросают канат, который оборачивают около тумбы, после чего достаточно усилий и одного человека, чтобы под действием силы трения остановить даже очень большой корабль.
Не вдаваясь в физику, будем считать, что уравновешивание силы корабля и человека происходит по закону F=F0x3n, где F – сила корабля, F0 – сила человека, а n – число витков. Найти, сколько следует сделать витков каната, чтобы человек с приложением силы 8H смог остановить у причала корабль с силой 120H. Совершенно очевидно, что для ответа на поставленный вопрос нам необходимо найти n из уравнения 120=8х3.
Полученный математический результат означает, что необходимо сделать 3(не меньше) оборота каната вокруг тумбы.
Разумеется, на практике никто логарифмов не считает, и, как правило, при причаливании корабля человек накручивает количество витков, исходя из своего опыта. Однако это не означает, что так будет всегда: возможно появление нестандартных ситуаций, а для того чтобы их спрогнозировать и дать соответствующую рекомендацию, нужны знания, а не только опыт.
Логарифмическая функция 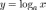 незаменима и во многих других областях человеческой деятельности: решение дифференциальных уравнений, классификация значений величин (например, частота и интенсивность звука), аппроксимация различных зависимостей, теория информации, теория вероятностей и т. д. Эта функция относится к числу элементарных, она обратна по отношению к показательной функции. Чаще всего используются вещественные логарифмы с основаниями
незаменима и во многих других областях человеческой деятельности: решение дифференциальных уравнений, классификация значений величин (например, частота и интенсивность звука), аппроксимация различных зависимостей, теория информации, теория вероятностей и т. д. Эта функция относится к числу элементарных, она обратна по отношению к показательной функции. Чаще всего используются вещественные логарифмы с основаниями  (двоичный),
(двоичный),  (натуральный логарифм) и
(натуральный логарифм) и 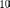 (десятичный).
(десятичный).
Логарифмические зависимости в науке и в природе:
• Теория чисел
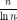 Распределение простых чисел асимптотически подчиняется простым законам:
Распределение простых чисел асимптотически подчиняется простым законам:
- Число простых чисел в интервале от 1 до  приблизительно равно
приблизительно равно
- k-е простое число приблизительно равно 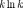 .
.
• Математический анализ
Логарифмы нередко возникают при нахождении интегралов и при решении дифференциальных уравнений. Примеры:
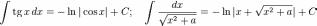
• Теория вероятностей и статистика
В статистике и теории вероятностей логарифм входит в ряд практически важных вероятностных распределений.
Логарифмическое распределение (используется в физике и генетике);
Логнормальное распределение (используется в ситуациях, когда исследуемая величина есть произведение нескольких независимых положительных случайных переменных);
Закон Бенфорда («закон первой цифры») (описывает вероятность появления определённой первой значащей цифры при измерении реальных величин);
Логарифмическая функция правдоподобия (для оценки неизвестного параметра широко применяются метод максимального правдоподобия);
Закон Хинчина-Колмогорова (описывает флуктуации при случайном блуждании)
• Информатика и вычислительная математика
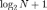 В информатике: единица измерения информации (бит). Например, для хранения в компьютере натурального числа
В информатике: единица измерения информации (бит). Например, для хранения в компьютере натурального числа 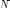 (в обычном для компьютера двоичном формате) понадобится битов.
(в обычном для компьютера двоичном формате) понадобится битов.
Оценка асимптотической сложности рекурсивных алгоритмов, быстрая сортировка, быстрое преобразование Фурье и т. п.
Обычно числовые значения хранятся в памяти компьютера или специализированного процессора в формате с плавающей запятой. Если, однако, сложение и вычитание для группы данных выполняются редко, а умножение, деление, возведение в степень и извлечение корня — гораздо чаще, тогда имеет смысл рассмотреть возможность хранения таких данных в логарифмическом формате. В этом случае вместо числа хранится логарифм его модуля и знак, и скорость вычислений благодаря свойствам логарифма значительно повышается. Логарифмический формат хранения был использован в нескольких системах, где доказал свою эффективность
• Фракталы и размерность
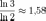 Логарифмы помогают выразить размерность Хаусдорфа для фрактала. Например, рассмотрим треугольник Серпинского, который получается из равностороннего треугольника последовательным удалением аналогичных треугольников, линейный размер каждого из которых на каждом этапе уменьшается вдвое. Размерность результата определяется по формуле:
Логарифмы помогают выразить размерность Хаусдорфа для фрактала. Например, рассмотрим треугольник Серпинского, который получается из равностороннего треугольника последовательным удалением аналогичных треугольников, линейный размер каждого из которых на каждом этапе уменьшается вдвое. Размерность результата определяется по формуле:
Графики логарифмов и их свойства
|
|
|
a 1 |
|
| D(f) | (0; + ∞) | (0; + ∞) | (0; + ∞) |
| E(f) | (- ∞ ; + ∞ ) | (- ∞ ; + ∞ ) | (- ∞ ; + ∞ ) |
| Четность функции | Ни чётная, ни нечётная | Ни чётная, ни нечётная | Ни чётная, ни нечётная |
| Монотонность | Убыв. на (0; + ∞) | Возр. на (0; + ∞) | Возр. на (0; + ∞) |
| Ограниченность | Не ограничена | Не ограничена | Не ограничена |
| Непрерывность | Непрерывна | Непрерывна | Непрерывна |
| Выпуклость | Выпукла вниз | Выпукла вверх | Выпукла вверх |
| и | Нет | Нет | Нет |
| Асимптоты | Вертикальная x=0 Горизонтальная - нет | Вертикальная x=0 Горизонтальная - нет | Вертикальная x=0 Горизонтальная - нет |
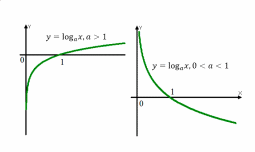
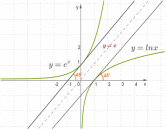 График натурального логарифма (y=ln x)
График натурального логарифма (y=ln x)
График натурального логарифма (функции y = ln x) получается из графика экспоненты зеркальным отражением относительно прямой y = x.
Натуральный логарифм определен при положительных значениях переменной x. Он монотонно возрастает на своей области определения.
При x → 0 пределом натурального логарифма является минус бесконечность ( – ; ∞ ). При x → + ∞ пределом натурального логарифма является плюс бесконечность ( +; ∞ ).
При больших x логарифм возрастает довольно медленно. Любая степенная функция xa с положительным показателем степени a растет быстрее логарифма.
Натуральным логарифмом называется логарифм по основанию  . Такие логарифмы обозначаются символом ln. Запись
. Такие логарифмы обозначаются символом ln. Запись 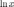 означает тоже самое, что и
означает тоже самое, что и 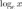 .
.
Основание натурального логарифма - число е.
Свойства натурального логарифма:
1° 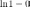
2° 
3°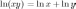
4°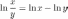
5°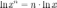
6°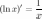
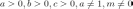
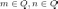 Основные свойства логарифмов
Основные свойства логарифмов
если
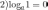
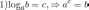
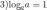
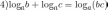
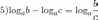
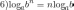
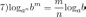
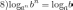
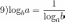
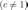
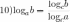
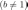
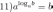





 по основанию
по основанию  – показатель степени, в которую нужно возвести число
– показатель степени, в которую нужно возвести число 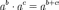 . Индийский математик VIII века Вирасена, исследуя степенные зависимости, опубликовал таблицу целочисленных показателей (то есть, фактически, логарифмов) для оснований 2, 3, 4.
. Индийский математик VIII века Вирасена, исследуя степенные зависимости, опубликовал таблицу целочисленных показателей (то есть, фактически, логарифмов) для оснований 2, 3, 4.


 Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.
Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.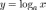 незаменима и во многих других областях человеческой деятельности: решение дифференциальных уравнений, классификация значений величин (например, частота и интенсивность звука), аппроксимация различных зависимостей, теория информации, теория вероятностей и т. д. Эта функция относится к числу элементарных, она обратна по отношению к показательной функции. Чаще всего используются вещественные логарифмы с основаниями
незаменима и во многих других областях человеческой деятельности: решение дифференциальных уравнений, классификация значений величин (например, частота и интенсивность звука), аппроксимация различных зависимостей, теория информации, теория вероятностей и т. д. Эта функция относится к числу элементарных, она обратна по отношению к показательной функции. Чаще всего используются вещественные логарифмы с основаниями  (двоичный),
(двоичный),  (натуральный логарифм) и
(натуральный логарифм) и 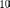 (десятичный).
(десятичный).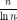 Распределение простых чисел асимптотически подчиняется простым законам:
Распределение простых чисел асимптотически подчиняется простым законам: приблизительно равно
приблизительно равно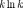 .
.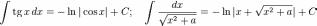
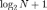 В информатике: единица измерения информации (бит). Например, для хранения в компьютере натурального числа
В информатике: единица измерения информации (бит). Например, для хранения в компьютере натурального числа 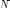 (в обычном для компьютера двоичном формате) понадобится битов.
(в обычном для компьютера двоичном формате) понадобится битов.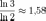 Логарифмы помогают выразить размерность Хаусдорфа для фрактала. Например, рассмотрим треугольник Серпинского, который получается из равностороннего треугольника последовательным удалением аналогичных треугольников, линейный размер каждого из которых на каждом этапе уменьшается вдвое. Размерность результата определяется по формуле:
Логарифмы помогают выразить размерность Хаусдорфа для фрактала. Например, рассмотрим треугольник Серпинского, который получается из равностороннего треугольника последовательным удалением аналогичных треугольников, линейный размер каждого из которых на каждом этапе уменьшается вдвое. Размерность результата определяется по формуле: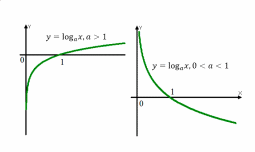
 График натурального логарифма (y=ln x)
График натурального логарифма (y=ln x) . Такие логарифмы обозначаются символом ln. Запись
. Такие логарифмы обозначаются символом ln. Запись 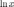 означает тоже самое, что и
означает тоже самое, что и 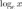 .
.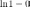

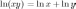
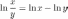
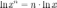
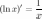
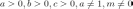
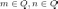 Основные свойства логарифмов
Основные свойства логарифмов