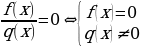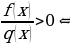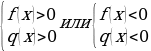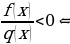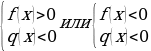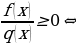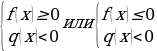| ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА |
| Линейные уравнения | Линейные неравенства |
| Определение. Линейное уравнение с одной переменной x называют уравнение вида 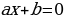 , где a и b - действительные числа. , где a и b - действительные числа. | Определение. Линейное неравенство с одной переменной x называют неравенство вида 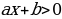 ( ( 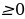 ) ) |
| Если 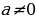 , то линейное уравнение называют также уравнением первой степени. , то линейное уравнение называют также уравнением первой степени. | Если 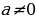 , то линейное неравенство называют также неравенством первой степени. , то линейное неравенство называют также неравенством первой степени. |
| Схема решения | Схема решения (для случая 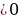 ) ) |
| 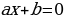 , тогда , тогда 
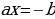  
 a=0 a a=0 a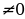  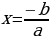  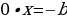 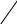  Единственный Единственный 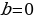 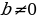 корень корень  
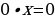 корней нет корней нет
| x – любое число | | Бесконечное множество корней |
| 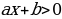 , тогда , тогда 
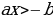   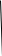
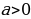 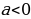   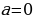 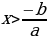 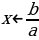 
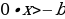  
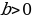 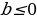  
x – любое решений число нет
|
| КВАДРАТНЫЕ УРАВНЕНИЯ |
| Определение. Уравнение виды ax2+bx+c=0, где x - переменная, a, b и c – некоторые числа, причем a 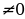 , называется квадратным. , называется квадратным. |
| Схема решения уравнения общего вида | Схема решения приведенного уравнения (a = 0) |
| 
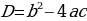 – дискриминант – дискриминант 
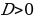 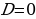 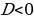  
 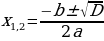 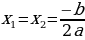 Корней Корней Т.е. два разных корня нет 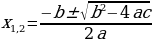 При подсчете ко- При подсчете ко- два различных личества решений корня считается за одно значение корня
| 
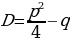 – дискриминант приведенного уравнения – дискриминант приведенного уравнения
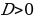 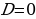 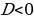   
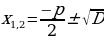 , т.е. , т.е. 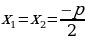 Корней Корней 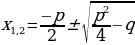 два различных нет два различных нет Два различных корня корня |
| Теорема Виета |
| В общем виде | Для приведенного уравнения |
| Е сли сли 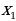 и и 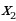 - корни квадратного - корни квадратного 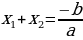 уравнения ax2+bx+c=0, то 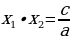
| Е сли сли 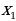 и и 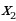 - корни приведенного - корни приведенного 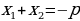 квадратного уравнения 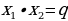 x2+px+q=0, то
|
| Обратная теорема |
| Если сумма каких-то двух корней 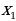 и и 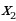 равна равна 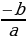 , а произведение равно , а произведение равно 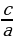 , то эти числа являются корнями квадратного уравнения ax2+bx+c=0. , то эти числа являются корнями квадратного уравнения ax2+bx+c=0. | Если сумма каких-то двух корней 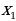 и и 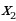 равна равна 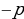 , а произведение равно q , то эти числа являются корнями приведенного квадратного уравнения x2+px+q=0. , а произведение равно q , то эти числа являются корнями приведенного квадратного уравнения x2+px+q=0. |
| Разложение квадратного трёхчлена на множители |
| Если 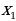 и и 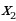 - корни квадратного трхчлена ax2+bx+c (т.е. корни уравнения ax2+bx+c=0), то ax2+bx+c= a(x - - корни квадратного трхчлена ax2+bx+c (т.е. корни уравнения ax2+bx+c=0), то ax2+bx+c= a(x - 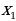 )(x - )(x - 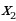 ) ) | Пример. 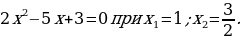 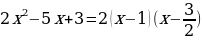 |
| Если дискриминант квадратного трёхчлена равен нулю, то 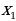 = = 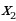 и тогда ax2+bx+c= a(x - и тогда ax2+bx+c= a(x - 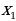 )2 )2 | Пример. 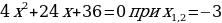 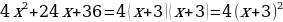 |
| КВАДРАТНЫЕ НЕРАВЕНСТВА |
| Определение. Неравенство вида ax2+bx+c 0 ( 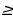 0) называют квадратным, если a 0) называют квадратным, если a 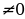 . . |
| Схема решения (метод интервалов) |
| Решение: Пусть f(x) = ax2+bx+c Найти ОДЗ. Найти нули функции, т.е. f(x) =0 Отметить нули функции и ОДЗ на числовой прямой, и найти знак функции на каждом из получившихся интервалов, на которые разбивается числовая прямая. Записать ответ, учитывая знак неравенства.
|
| ДРОБНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА |
| Схема решения |
|   Решение Решение дробных уравнений дробных неравенств
Использование Использование Использование равносильных Использование у  равнений-следствий свойств соответ- преобразований метода интервалов равнений-следствий свойств соответ- преобразований метода интервалов 1.Приводим к виду ствующих функций 1. Фиксируем ОДЗ исходного 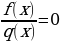 уравнения (неравенства). уравнения (неравенства). 2.Находим корни 2. Приводим к виду 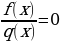 уравнения 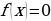 (, (, 3.Выполняем проверку (неравенства) на ОДЗ исходного подстановкой корней или выполняем равносильные в исходное уравнение. преобразования так, чтобы ввести удобную замену переменных.
|
| Равносильные преобразования простейших дробных уравнений и неравенств |
| 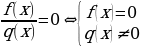 | 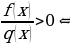 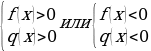 | 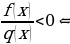 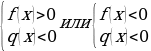 | 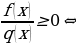 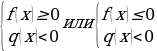 |







 , где a и b - действительные числа.
, где a и b - действительные числа. (< 0, ≤ 0, ≥0
(< 0, ≤ 0, ≥0 )
) , то линейное уравнение называют также уравнением первой степени.
, то линейное уравнение называют также уравнением первой степени.
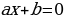 , где a и b - действительные числа.
, где a и b - действительные числа.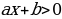 (
( 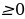 )
)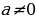 , то линейное уравнение называют также уравнением первой степени.
, то линейное уравнение называют также уравнением первой степени.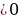 )
)
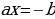


 a=0 a
a=0 a

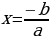

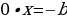
 Единственный
Единственный 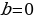
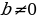 корень
корень

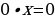 корней нет
корней нет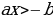


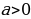
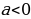

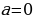
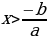
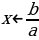
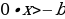


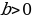
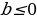



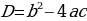 – дискриминант
– дискриминант
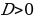
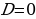
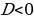



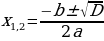
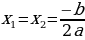 Корней
Корней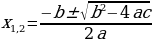 При подсчете ко-
При подсчете ко-
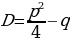 – дискриминант приведенного уравнения
– дискриминант приведенного уравнения


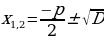 , т.е.
, т.е. 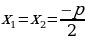 Корней
Корней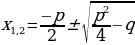 два различных нет
два различных нет сли
сли 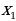 и
и 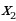 - корни квадратного
- корни квадратного 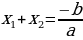
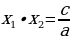
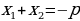
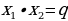
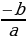 , а произведение равно
, а произведение равно 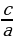 , то эти числа являются корнями квадратного уравнения ax2+bx+c=0.
, то эти числа являются корнями квадратного уравнения ax2+bx+c=0.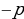 , а произведение равно q , то эти числа являются корнями приведенного квадратного уравнения x2+px+q=0.
, а произведение равно q , то эти числа являются корнями приведенного квадратного уравнения x2+px+q=0.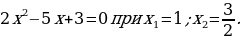
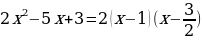
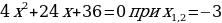
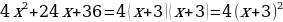
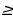 0) называют квадратным, если a
0) называют квадратным, если a 





 равнений-следствий свойств соответ- преобразований метода интервалов
равнений-следствий свойств соответ- преобразований метода интервалов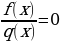 уравнения (неравенства).
уравнения (неравенства).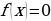 (,
(,