Методическая разработка материалов к переводной аттестации по геометрии в 7 классе и система работы

Муниципальное общеобразовательное учреждение

«Киришский лицей»

«Методическая разработка материалов к переводной аттестации по геометрии

в 7 классе и система работы».

Выполнили: Толмачева Е.В.

учитель математики

МОУ «Киришский лицей»

Копеина Н.В.

учитель математики

МОУ «Киришский лицей»

Кириши

2021 г.

Методическая разработка материалов к переводной аттестации по геометрии в 7 классе и система работы.

Всё чаще мы говорим о качестве образования, которое оценивается по уровню полученных знаний, по сформированности творческих качеств личности (компетенций), направленных на выполнение социальных и профессиональных задач.

Федеральный государственный образовательный стандарт устанавливает требования к результатам освоения обучающимися основной образовательной программы основного общего образования: предметные, метапредметные и личностные. Нам хотелось бы выделить прежде всего метапредметные результаты, на которые мы делаем акцент при изучении геометрии:

• умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности;

• умение самостоятельно планировать пути  достижения целей,  в том числе альтернативные,  осознанно выбирать  наиболее эффективные способы решения учебных и познавательных задач;

• умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы  действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;

• умение оценивать правильность выполнения учебной задачи,  собственные возможности её решения;

•  умение  определять понятия, создавать обобщения, устанавливать аналогии, классифицировать,   самостоятельно выбирать основания и критерии для классификации, устанавливать причинно-следственные связи, строить  логическое рассуждение, умозаключение (индуктивное, дедуктивное  и по аналогии) и делать выводы;

• умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач;

• смысловое чтение;

• умение организовывать  учебное сотрудничество и совместную деятельность с учителем и сверстниками;   работать индивидуально и в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов;  формулировать, аргументировать и отстаивать своё мнение;

• умение осознанно использовать речевые средства в соответствии с задачей коммуникации для выражения своих чувств, мыслей и потребностей; планирования и регуляции своей деятельности;  владение устной и письменной речью, монологической контекстной речью;

• формирование и развитие компетентности в области использования информационно-коммуникационных технологий (далее ИКТ– компетенции);

Актуальность данной методической разработки. На протяжении последних лет количество задач, направленных на диагностику обученности геометрии значительно увеличилось. Мониторинг результатов ОГЭ и ЕГЭ говорит о необходимости модернизации преподавания геометрии в школе.

Геометрия как школьный предмет всегда считался одним из самых сложных в школьном курсе.

В 7 классе начинается изучение систематического курса геометрии. Основная сложность данного этапа заключена в том, что при изложении геометрического материала учащиеся впервые встречаются с большим количеством определений, аксиом, теорем, здесь появляются первые строго построенные доказательства геометрических фактов. Материал, который изучается в 7 классе, находит широкое применение в последующем курсе геометрии. Отсюда и вытекает необходимость того, чтобы знания по геометрии, полученные школьниками в 7 классе, были глубокими, прочными и осмысленными.

Значимость и актуальность проблемы обучения логике и грамотному построению рассуждения заставила учителей математики пересмотреть подходы к организации контроля знаний, уделяя особое внимание устным ответам на зачетах, давая возможность каждому ученику «проговорить» математическую терминологию.

На методическом совете МОУ «Киришский лицей» было принято решение о включении в расписание ежегодной устной переводной аттестации семиклассников по геометрии. В связи с этим была организована работа творческой группы учителей математики. Каждый внес свои предложения, мы их обсудили и начали работать.

Цель: контроль усвоения теоретических знаний и их практического применения на уроках геометрии в 7 классе.

Задачи:

• научить обучающихся грамотной устной речи, логическому построению рассуждений и их письменной записи

• сформировать навыки владения математической терминологией.

• мотивировать учащихся к изучению предмета «Геометрия»;

• научить обучающихся прогнозированию результатов своего интеллектуального труда.

Мы разработали теоретические вопросы, подобрали дифференцированные задачи. Все темы билетов, виды задач были размещены на информационных стендах в кабинетах математики. У каждого ученика были заведены тетради, где они записывании формулировки теорем и грамотно оформляли их доказательство, решали задачи и выполняли геометрические построения с помощью циркуля и линейки, записывая ход построения. Все теоретические вопросы и практические задания ребята отвечали устно во внеурочное время, велся учет знаний. Задачи ученики решали дома в удобное для них время и сдавали на проверку: исправлялись ошибки, давались рекомендации по решению, лучшие поощрялись отметкой.

Большая роль отводилась консультациям, где ребята задавали вопросы, работали с учебником, выполняли на доске практические задания с помощью чертежных инструментов, разбирались сложные моменты задач. Надо отметить, что не только учитель работал, но и ученики другу давали советы, где найти материал, рассказывали план решенной ими задач, показывали построение фигур.

Практическая значимость работы: материалы, представленные в работе, могут использоваться учителями математики для переводной аттестации в 7 классе по геометрии.

Билеты по геометрии 7 класс.

Билет 1.

1. Определение и свойство смежных углов.

2. Найти  С АВС, если А = 65°,  В = 57°.

3. Найти стороны треугольника, если они относятся как 2:3:4, а периметр его равен 27дм.

4. Постройте прямую, перпендикулярную данной, и проходящую через точку, не лежащую на данной прямой.

Билет 2.

1. Определение и свойство вертикальных углов.

2. Найти сторону равнобедренного треугольника, если две его другие стороны равны

5см и 3см.

3. Найти углы ∆ АВС, если углы А, В, С относятся как 2:3:4 соответственно.

4. Постройте угол, равный данному.

Билет3.

1. Сформулировать и доказать признак равенства треугольников по двум сторонам и

углу между ними.

2. Один из смежных углов в 2 раза больше другого. Найти эти углы.

3. Периметр равнобедренного треугольника 46см, а боковая сторона его больше

основания на 8см больше. Вычислите длины сторон треугольника.

4. Постройте биссектрису угла.

Билет 4.

1. Сформулировать и доказать признак равенства треугольников по стороне и двум

прилежащим к ним углам.

2. Основание равнобедренного треугольника 6см, а боковая сторона на 3см больше.

Найти периметр треугольника.

3. Даны две пересекающиеся прямые. Сумма двух образовавшихся при этом углов равна

288°. Вычислите сумму острых и сумму тупых углов.

4. Начертите тупой угол АВС и отметьте точку D вне его. С помощью чертежного

угольника через точку D проведите прямые, перпендикулярные к прямым АВ и ВС.

Билет 5.

1. Сформулировать и доказать признак равенства треугольников по трем сторонам.

2. Чему равно основание равнобедренного треугольника АВС, если его периметр равен 86см, а длина боковой стороны 28см.

3. Две параллельные прямые пересечены третьей. Один из острых углов 47°. Найти величины всех получившихся при пересечении двух прямых третьей углов.

4. С помощью транспортира начертите угол, равный 132° и с помощью циркуля и линейки проведите биссектрису одного из смежных с ним углов.
   
   

Билет 6.

1. Определение параллельных прямых. Признаки параллельности двух прямых (формулировки всех признаков, доказательство одного из них).

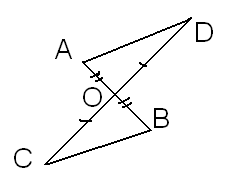
2. На рисунке АО = ОВ, СО = ОD. Докажите равенство получившихся треугольников.

3. На отрезке АС отмечена точка В.Известно, что АС = 16см, АВ = 11см. Найти длину

ВС и сравнить его с длиной АВ, а также найти расстояние от точки В до середины

отрезка АС.

4. Постройте прямоугольный треугольник по гипотенузе и острому углу.

Билет 7.

1. Определение параллельных прямых. Свойства параллельности двух прямых (формулировки всех свойств, доказательство одного из них).

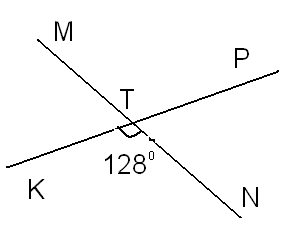
2. Найти градусные меры углов MTK и MTP.

1. В треугольниках равны по две стороны и углу между ними соответственно. Докажите, что отрезки, соединяющие вершины равных углов и середины противоположных сторон, равны.

2. С помощью циркуля и линейки постройте угол, равный 150°.
   
   

Билет 8.

1. Теорема о сумме углов треугольника.

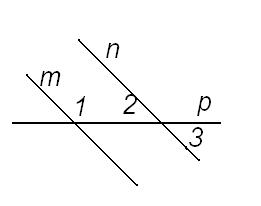
2. Дано: m║n, 1= 125°. Вычислить градусные меры углов 2 и 3.

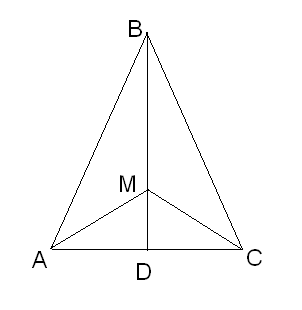
1. В равнобедренном треугольнике АВС с основанием АС на медиане BD выбрана точка М. Докажите равенство треугольников АВМ и СВМ.

2. Постройте треугольник по катету и прилежащему к нему

острому углу.

Билет 9.

1. Свойство углов при основании равнобедренного треугольника.

2. На отрезке АС отмечена точка В.Известно, что АС = 16см, АВ = 11см. Найти длину ВС и сравнить его с длиной АВ.

3. Прямые с и d пересекаются в точке О. Сумма градусных мер образовавшихся двух острых углов равна 76°. Найти величины образовавшихся острых и тупых углов.

4. С помощью циркуля и линейки постройте угол, равный 105°.
   
   

Билет 10.

1. Теорема о соотношениях между сторонами и углами треугольника.

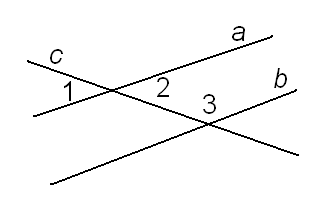
2. Дано: а║b, 1 = 65°. Вычислить градусные меры углов 2 и 3.

3. Найдите углы равнобедренного треугольника, если градусные меры двух из них

относятся как 2:5.

4. Построить треугольник по двум сторонам и углу между ними.

Билет 11.

1. Неравенство треугольника.

2. Внешний угол при вершине равнобедренного треугольника равен 100°. Найдите углы треугольника.

3. Периметр равнобедренного треугольника 58см. Его основание больше боковой стороны на 4см. Вычислите длины сторон треугольника.

4. Построить треугольник по стороне и прилежащим к ней углам.
   
   

Билет 12.

1.Перпендикулярные прямые. Определение и свойство.

2. Высота прямоугольного треугольника делит прямой угол на два угла, один из которых

на 40° больше другого. Найти острые углы данного треугольника.

3. На рисунке АО = СО, BO = OD. Докажите, что АD || ВС.

4. Построить треугольник по трем сторонам.

Билет 13.

1. Свойства медианы, биссектрисы и высоты равнобедренного треугольника (формулировки

всех свойств, доказательство одного из них).

2. Треугольники АВС и MNK равны. Известно, что АВ = MN, ВС = NК, С = 75°,

МК = 4 см. Найдите АС и К.

3. В прямоугольном треугольнике градусные меры внешних углов относятся как 3:4:5.

Найдите острые углы этого треугольника.

4. Постройте равнобедренный треугольник по основанию и медиане, проведённой

к основанию.

Билет 14.

1. Прямоугольный треугольник. Его свойства (формулировки всех свойств,

доказательство одного из них).

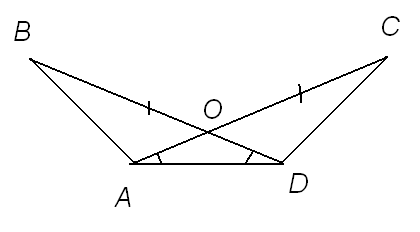
2. На рисунке АС = BD, углы САD и BDA равны. Докажите равенство треугольников ABD

и АСD.

3. В прямоугольном треугольнике сумма двух внешних углов при различных вершинах

равна 200°. Найдите острые углы этого треугольника.

4. Постройте равнобедренный треугольник по основанию и углу, прилежащему

к основанию.

Билет 15.

1. Признаки равенства прямоугольных треугольников (формулировки всех признаков,

доказательство одного из них).

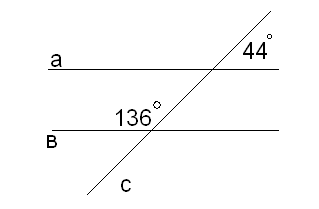
2. По данному рисунку докажите, что а || в

3. ∆АВС – равнобедренный с основанием АС, ∟АВД=∟СВЕ. Докажите, что

∆АВД=∆СВЕ.

В

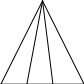
А Д Е С

4. Постройте равнобедренный треугольник по основанию и боковой стороне.

Билет 16.

1.Определение внешнего угла треугольника. Его свойство.

2. Прямые а и в параллельны, 1 = 132°. Найти 2, 3.

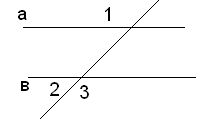
3. На основании АС равнобедренного ∆АВС отложены равные отрезки АД и СЕ.

Докажите, что ∆ВАД=∆ВСЕ.

4. Постройте прямоугольный треугольник по двум катетам.

Билет 17.

1. Расстояние от точки до прямой. Расстояние между двумя параллельными прямыми.

2. Найдите острые углы прямоугольного треугольника, если один из них на 20⁰ больше

другого.

3. Точка М лежит на медиане ВК равнобедренного ∆АВС (АС – основание). Докажите,

что ∆АВМ=∆СВМ.

4. Постройте угол, равный данному.

Приложение (для стендов в кабинете математики)

1.Определение и свойство смежных углов.

2.Определение и свойство вертикальных углов.

3.Сформулировать и доказать признак равенства треугольников по двум сторонам и углу между ними.

4.Сформулировать и доказать признак равенства треугольников по стороне и двум прилежащим к ним углам.

5.Сформулировать и доказать признак равенства треугольников по трем сторонам.

6.Определение параллельных прямых. Признаки параллельности двух прямых (формулировки всех признаков, доказательство одного из них).

7.Определение параллельных прямых. Свойства параллельности двух прямых (формулировки всех свойств, доказательство одного из них).

8.Теорема о сумме углов треугольника.

9.Свойство углов при основании равнобедренного треугольника.

10.Теорема о соотношениях между сторонами и углами треугольника.

11.Неравенство треугольника.

12.Перпендикулярные прямые. Определение и свойство.

13.Свойства медианы, биссектрисы и высоты равнобедренного треугольника (формулировки всех свойств, доказательство одного из них).

14. Прямоугольный треугольник. Его свойства (формулировки всех свойств, доказательство одного из них).

15. Признаки равенства прямоугольных треугольников (формулировки всех признаков, доказательство одного из них).

16. Определение внешнего угла треугольника. Его свойство.

17.Расстояние от точки до прямой. Расстояние между двумя параллельными прямыми.

«5» - ответ полный, логичный, самостоятельный. Допустимы 2 недочета.

«4» - ответ полный, логичный, с наводящими вопросами. Допустима одна грубая ошибка.

«3» - даны четкие определения и четко сформулированы теоремы.

1. Найти  С АВС, если А = 65°,  В = 57°.
   
   

2. Найти сторону равнобедренного треугольника, если две его другие стороны равны 5см и 3см.
   
   

3. Один из смежных углов в 2 раза больше другого. Найти эти углы.
   
   

4. Основание равнобедренного треугольника 6см, а боковая сторона на 3см больше. Найти периметр треугольника.
   
   

5. Чему равно основание равнобедренного треугольника АВС, если его периметр равен 86см, а длина боковой стороны 28см.
   
   

6. Дано: m║n, 1= 125°. Вычислить градусные меры углов 2 и 3.

1. Найти градусные меры углов MTK и MTP.

8. На рисунке АО = ОВ, СО = ОD. Докажите равенство получившихся треугольников.

9. На отрезке АС отмечена точка В.Известно, что АС = 16см, АВ = 11см. Найти длину ВС и сравнить его с длиной АВ.

10. Дано: а║b, 1 = 65°. Вычислить градусные меры углов 2 и 3.

11. Внешний угол при вершине равнобедренного треугольника равен 100°. Найдите углы треугольника.

12. Высота прямоугольного треугольника делит прямой угол на два угла, один из которых на 40° больше другого. Найти острые углы данного треугольника.

1. На отрезке АВ отмечены точки C и D. Найдите длину отрезка CD, если АВ = 8,4 см,
   АС = 2,1 см , BD = 1,3 см. Какая из данных точек лежит между точками В и С?

1. Треугольники АВС и MNK равны. Известно, что АВ = MN, ВС = NК, С = 75°,
   МК = 4 см. Найдите АС и К.

1. На рисунке АС = BD, углы САD и BDA равны. Докажите равенство треугольников ABD и АСD.

1. По данному рисунку докажите, что а || в
   

2. Прямые а и в параллельны, 1 = 132°. Найти 2, 3.
   

3. Прямые а и в параллельны, 1 + 2 = 250°. Найти 3.
   

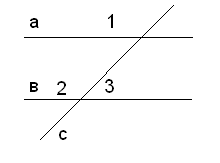
4. На данном рисунке 1 = 82°, 2 = 119°, 3 = 82°.
   а). Найдите 4.
   б). Сколько углов, равных 4, изображено на рисунке? Отметьте эти углы.
   

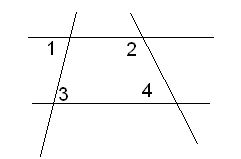
5. Найдите острые углы прямоугольного треугольника, если один из них на 60⁰ больше другого.

6. Внешний угол при основании равнобедренного треугольника равен 140⁰. Найдите углы треугольника.

7. Определите, является ли треугольник АВС тупоугольным, если два его внешних угла равны 135° и 160°.

8. Высота прямоугольного треугольника делит прямой угол на два угла, один из которых в 4 раза больше другого. Найдите острые углы данного треугольника.

9. АВС = 120°. Из точки А проведен перпендикуляр АМ к прямой ВС. Найдите длину отрезка ВМ, если АВ = 18 см.

10. Прямоугольные треугольники АВС и ABD имеют общую гипотенузу АВ. Известно, что АВ – биссектриса CAD. Докажите, что ВА – биссектриса CВD.
    

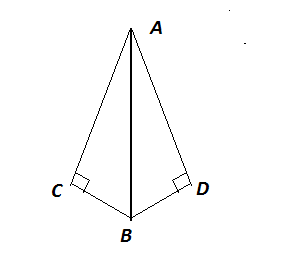
11. В треугольнике АВС А = 70°, С = 55°. а).Докажите, что треугольник АВС – равнобедренный, и укажите его основание. б). ВМ – высота данного треугольника. Найдите углы, на которые она делит АВС.

12. Отрезки АВ и CD пересекаются в точке О, которая является серединой каждого из них.
    а). Докажите, что треугольники АОС и BOD равны.
    б). Найдите ОАС, если ODB = 20°, AOC = 115°.

13. В равнобедренном треугольнике с периметром 64 см одна из сторон равна 16 см. найдите длину боковой стороны треугольника.

1. Найти углы ∆ АВС, если углы А, В, С относятся как 2:3:4 соответственно.
   
   

2. Найти стороны треугольника, если они относятся как 2:3:4, а периметр его равен 27дм.
   
   

3. Даны две пересекающиеся прямые. Сумма двух образовавшихся при этом углов равна 288°. Вычислите сумму острых и сумму тупых углов.
   
   

4. Периметр равнобедренного треугольника 46см, а боковая сторона его больше основания на 8см больше. Вычислите длины сторон треугольника.
   
   

5. Периметр равнобедренного треугольника 58см. Его основание больше боковой стороны на 4см. Вычислите длины сторон треугольника.
   
   

6. Две параллельные прямые пересечены третьей. Один из острых углов 47°. Найти величины всех получившихся при пересечении двух прямых третьей углов.
   
   

7. Прямые с и d пересекаются в точке О. Сумма градусных мер образовавшихся двух острых углов равна 76°. Найти величины образовавшихся острых и тупых углов.
   
   

8. На отрезке АС отмечена точка В.Известно, что АС = 16см, АВ = 11см. Найти длину ВС и сравнить его с длиной АВ, а также найти расстояние от точки В до середины отрезка АС.
   
   

9. Через вершину равнобедренного треугольника проведена прямая, параллельная основанию. Угол при вершине треугольника равен 120°. Найти градусные меры образовавшихся углов.
   
   

10. Два внешних угла треугольника равны 150° и 78°. Найти углы, которые биссектриса наибольшего угла треугольника образует с его наибольшей стороной.
    
    

11. В прямоугольном треугольнике АВС В прямой,  С 30°, сторона ВС равна 18см. Найти длины отрезков, на которые биссектриса AD делит катет ВС.

12. На рисунке BN – биссектриса угла МВС. а). Найдите АВМ, если MBN = 55°. б). Постройте АВК, вертикальный с NBC, и найдите его градусную меру. в). Найдите градусную меру СВК.
    

13. В треугольниках равны по две стороны и углу между ними соответственно. Докажите, что отрезки, соединяющие вершины равных углов и середины противоположных сторон, равны.

14. В равнобедренном треугольнике АВС с основанием АС на медиане BD выбрана точка М. Докажите равенство треугольников АВМ и СВМ.

15. На рисунке АО = СО, BO = OD. Докажите, что АD || ВС.

1. На рисунке 1 - 2 = 20° , 3 = 80°. Параллельны ли прямые а и в?
   

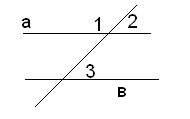
2. В треугольнике АВС B = 90°. Через вершину С проходит прямая, которая параллельна стороне АВ и образует с АС угол в 36°. Найдите углы А и С.

3. По данным рисунка найдите  х.
   

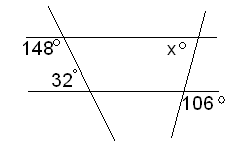
4. Дан АВС, равный 82°. Через точку D, лежащую на его биссектрисе, проведена прямая, параллельная прямой ВС и пересекающая сторону АВ в точке Е. Найдите углы треугольника BDE.

5. Из точек А и В, лежащих на одной из сторон данного острого угла, проведены перпендикуляры АС и BD ко второй стороне угла.
   а). Докажите, что АС параллельна BD.
   б). Найдите ABD, если CAB = 125°.

6. Найти углы равнобедренного треугольника, если один из них на 90° больше другого.

7. В прямоугольном треугольнике градусные меры внешних углов относятся как 3:4:5. Найдите острые углы этого треугольника.

8. Определите, является ли треугольник АВС тупоугольным, если его биссектрисы пересекаются в точке О и АОВ = 140°.

9. Найдите углы равнобедренного треугольника, если градусные меры двух из них относятся как 2:5.

10. В прямоугольном треугольнике сумма двух внешних углов при различных вершинах равна 200°. Найдите острые углы этого треугольника.

11. В прямоугольном треугольнике биссектриса наибольшего угла пересекает гипотенузу под углом 80°. Найдите острые углы данного треугольника.

12. В прямоугольном треугольнике АВС В = 90°, АВ = 8 см, АС = 16 см. Найдите углы, которые образует высота BH с катетами треугольника.

13. Прямоугольные треугольники АВС и ABD имеют общую гипотенузу АВ. Известно, что АС  BD. Докажите, что AD = BC.

14. В треугольнике АВС высота BD делит В на два угла, причем ABD = 40°, CBD = 10°.
    а). Докажите, что треугольник АВС – равнобедренный, и укажите его основание.
    б). Высоты данного треугольника пересекаются в точке О. найдите ВОС.

«5» - выполнен аккуратно с использованием инструментов чертеж, записано верно условие задачи, верно решена задача со всеми логическими объяснениями. Допустимы 2 недочета.

«4» - выполнен аккуратно с использованием инструментов чертеж, записано верно условие задачи, верно решена задача. Допустимы одна грубая ошибка или есть пробелы в пояснениях задачи.

«3» - выполнен аккуратно с использованием инструментов чертеж, записано верно условие задачи, решена задача, запись решения произвольная.

1. Разделите отрезок на две равные части.

2. Разделите угол на две равные части.
3. Постройте прямую, перпендикулярную данной, и проходящую через точку, не лежащую на данной прямой.
4. Постройте угол, равный данному.
5. Постройте биссектрису угла.
6. На луче ОА от точки В отложите отрезок ВС равный а.
7. Дан угол ВОС и точка А, в его внутренней области. Постройте луч АК, который пересекал бы луч ОВ, но не пересекал луч ОС, а также луч ОD так, чтобы угол DOC был развернутым.
8. Начертите угол АОВ равный 130°. Постройте с помощью линейки угол, смежный с углом АОВ. Чему равна его градусная мера.
9. От заданного луча отложите угол равный данному.
10. Начертите тупой угол АВС и отметьте точку D вне его. С помощью чертежного угольника через точку D проведите прямые, перпендикулярные к прямым АВ и ВС.
11. Отметьте точку С на прямой АВ так, чтобы точка В оказалась серединой отрезка АС.
12. С помощью транспортира начертите угол, равный 132° и с помощью циркуля и линейки проведите биссектрису одного из смежных с ним углов.
13. Постройте прямоугольный треугольник по гипотенузе и острому углу.
14. С помощью циркуля и линейки постройте угол, равный 150°.
15. Постройте треугольник по катету и прилежащему к нему острому углу.
16. С помощью циркуля и линейки постройте угол, равный 105°.
17. Построить треугольник по двум сторонам и углу между ними.

18. Построить треугольник по стороне и прилежащим к ней углам.
19. Построить треугольник по трем сторонам.