Методическая разработка системного внедрения в работу с дошкольниками технологии решения задач и установления логических связей «Круги Эйлера»

Методическая разработка

системного внедрения в работу с дошкольниками

технологии решения задач и установления логических связей

«Круги Эйлера»

Эффективное развитие интеллектуальных способностей детей дошкольного возраста — одна из актуальных задач современности. Дети с развитым интеллектом быстрее запоминают материал, более уверены в своих силах, легче адаптируются в новой обстановке, лучше подготовлены к школе. В настоящее время ФГОС ДО устанавливает нормы и положения, обязательные при реализации основной общеобразовательной программы дошкольного образования – формирование у детей дошкольного возраста предпосылок к учебной деятельности на этапе завершения ими дошкольного образования. В современных условиях от ребенка требуется не только владение знаниями, но и умение добывать эти знания самому и оперировать ими.

Одна из главных задач современной педагогики – это поиск возможностей использования скрытых резервов умственной деятельности детей, поиск путей эффективного обучения. И в сфере образования процесс обучения неизбежно должен быть более наглядным и динамичным. Одним из таких путей, интенсивно развивающим детское познание, может стать моделирование. Одним из показателей готовности ребенка к школьному обучению является формирование и развитие логического мышления. Логическое мышление формируется на основе образного мышления и является высшей стадией развития мышления. Достижение этой стадии - длительный и сложный процесс, так как полноценное развитие логического мышления требует не только высокой активности умственной деятельности, но и обобщенных знаний об общих и существенных признаках предметов и явлений действительности, которые закреплены в словах. Логическое мышление — это умение оперировать абстрактными понятиями, это мышление путем рассуждений и опровержений.

Способность логически мыслить позволяет: понимать происходящее вокруг, вскрывать существенные стороны, связи в предметах и явлениях окружающей действительности, делать умозаключения, решать различные задачи, проверять эти решения, доказывать, опровергать словом. Формировать и развивать логическое мышления можно с детьми любого уровня развития и любого возраста.

Одной из наиболее сложных мыслительных операций является классификация. Для достижения оптимального уровня развития этой мыслительной операции очень важно использовать такие средства оптимизации процесса обучения, которые дадут возможность ребенку зрительно представлять понятия. Поэтому одной из основных задач является овладение действием наглядного моделирования, так как именно наглядные модели наиболее приемлемы для занятий с дошкольниками, поскольку присущи детской деятельности.

Логическое мышление это мышление путем рассуждений, это строгое следование законам неумолимой логики, это безукоризненное построение причинно-следственных связей. Навыки, умения работать с моделями приобретенные в дошкольный период, будут служить фундаментом для универсальных учебных действий. Важнейшим является формирование и развитие логического мышления и способности «действовать в уме».

Наглядное   моделирование   ­   это   наиболее   универсальное средство,   т.к.   соответствует   специфике   наглядно   –   образного мышления   дошкольника.   Возникает цепочка: наглядно-­образное мышление, логическое мышление, способность   «действовать в уме». Приемы моделирования особенно эффективны для дошкольников, так как у них развито наглядно-действенное мышление, память носит непроизвольный характер, а мыслительные задачи решаются с преобладающей ролью внешних средств, наглядный материал усваивается лучше вербального. Метод наглядного моделирования помогает ребенку зрительно представить абстрактные понятия научиться работать с ними.

В работе наглядное моделирование, позволяет предотвратить быструю утомляемость, создать интерес к занятиям, научить детей видеть главное, систематизировать полученные знания. Дети очень легко и быстро понимают разного рода схематические изображения и с успехом пользуются ими.

Наглядная геометрическая иллюстрация объемов понятий и отношений между ними была предложена математиком, физиком и астрономом Леонардом Эйлером (1707 - 1781) и носит название кругов Эйлера. Он говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки. Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад.

Диаграммы Эйлера своим наглядным графическим изображением не только облегчают запоминание структуры различных сочетаний мыслей, но и помогают решению ряда задач, стоящих перед формальной логикой. Для наглядной геометрической иллюстрации объемов понятий и соотношений между ними используется диаграммы Эйлера (круги Эйлера). Если имеются какие-либо понятия А, В, С и т.д., то объем каждого понятия (множество) можно представить в виде круга, а отношения между этими объектами (множествами) – в виде пересекающихся кругов. Заштрихованные области показывают результат логических операций.

При помощи этого метода ученый решал сложнейшие математические задачи. Применение простых фигур позволяло свести решение любой, даже самой сложной задачи, к символической логике – максимальному упрощению рассуждений. Методика достаточно проста и используется в работе с детьми уже с 4-5 лет. При этом она же настолько удобна, что применяется даже в высшей математике. Основная цель использования диаграмм – практическое решение задач по объединению или пересечению множеств. Круги Эйлера - это графическая модель, с помощью которой можно наглядно отобразить отношения между понятиями или множествами объектов. А народная мудрость гласит: «Лучше один раз увидеть, чем сто раз услышать». Учитывая простоту и наглядность модели кругов Эйлера, ее с успехом используют в работе с дошкольниками.

Используя круги Эйлера, ребенок овладевает следующими элементами логических действий:

- анализ объектов с целью выделения признаков;

- синтез - составление целого из частей;

- выбор критериев для сравнения, классификации объектов;

- выведение следствий;

- установление причинно-следственных связей;

- построение логической цепи рассуждений.

Метод наглядного моделирования с помощью кругов Эйлера чаще всего используется для познавательного развития дошкольников. Начиная с 4-5 лет детям доступно решение простейших задач с кругами Эйлера, сначала с разъяснениями взрослых, а потом и самостоятельно. С детьми этого возраста уместны простые игры и упражнения, цель которых – закрепление представлений о свойствах предметов и геометрических фигур, тренировка в сравнении предметы по цвету, форме, размеру.

Овладение действием наглядного моделирования с помощью кругов Эйлера по формированию элементарных математических представлений лучше начать со сравнения предметов, у которых присутствует один общий признак (например, форма, цвет, размер, толщина), позже можно брать два и более признака, в зависимости от индивидуальных особенностей ребенка.

Для начала необходимо объяснить детям пространственные понятия «внутри круга» и «вне круга». Важно научить ребенка использовать частицу не для обозначения признака предметов вне круга.

Воспитатель кладет на пол обруч, обводит указкой то место, которое находится внутри обруча и рассказывает, что вся остальная часть пола находится вне обруча. Цель работы с одним кругом - учить классифицировать предметы по одному признаку, понимать и применять логическую операцию отрицания не, не называя её.

У каждого ребенка в руке один предмет. Дети по очереди располагают предметы в соответствии с заданием воспитателя. Расположите внутри обруча – все игрушки, а вне обруча – все остальные предметы. Затем проводится беседа по следующим вопросам:

 Какие предметы лежат внутри обруча? (игрушки)

 Какие предметы оказались вне обруча?

Неправильно, если дети начинают перечислять все предметы вне обруча.

- Выразите свойство всех фигур, лежащих вне круга, одним словом.  (Не игрушки)

Важно то, что внутри обруча лежат игрушки, и никаких других предметов там нет.

Затем мы приступаем к распределению предметов на два круга. Мы объясняем понятия «внутри круга» и «вне круга», используя уже два признака. Дети выполняют эти простые задания:

- Положите внутрь красного круга треугольные фигуры. 

- Положите внутрь синего круга красные фигуры. 

После того как все фигуры размещены, воспитатель задает два новых вопроса:

- Какие геометрические фигуры лежат внутри красного круга? (Внутри круга лежат треугольные фигуры). 

- Какие геометрические фигуры лежат внутри синего круга? (Внутри круга лежат красные фигуры). 

Этот ответ содержится в самом условии только что решенной задачи и формулируется обычно без особого труда. Правильного ответа на второй вопрос приходится ждать дольше.

- Какие геометрические фигуры лежат вне круга?  Выразите свойство всех фигур, лежащих вне круга, одним словом.  (Вне круга лежат НЕ треугольные, НЕ красные фигуры). 

Наша цель в данном случае - охарактеризовать свойство фигур, лежащих вне круга, через свойство фигур внутри круга. С дошкольниками можно использовать несколько моделей кругов:

а) Непересекающиеся круги;

б) Пересекающиеся круги;

в) Один круг вложен в другой.

Цель работы над задачами с двумя кругами - развить умение классифицировать предметы по двум свойствам, понимать и применять логическую операцию конъюнкции.

Теперь дети будут работать с двумя кругами или обручами разных цветов (синий, красный) с пересекающимися областями.

Перед решением задач необходимо выполнить ряд упражнений. Лучше всего такие упражнения проводить на групповых занятиях с использованием обручей.

- Обведите границу области внутри синего, но вне красного круга. 

- Обведите границу области внутри красного, но вне синего круга. 

- Обведите границу области внутри синего и внутри красного кругов. 

- Обведите границу области вне синего и вне красного кругов. 

После успешного выполнения подготовительных упражнений можно приступить к решению задач. После задачи с расположением фигур дети отвечают на четыре вопроса:

Какие фигуры лежат: 

- внутри обоих кругов; 

- внутри синего, но вне красного круга; 

- внутри красного, но вне синего круга; 

- вне обоих кругов? 

Фигуры надо называть, опираясь на два свойства - цвет и форму.

Наряду с логическими задачами можно ставить и задачи подсчета фигур.

Сколько фигур лежит: 

- внутри обоих кругов; 

- внутри синего, но вне красного круга; 

- внутри красного, но вне синего круга; 

- вне обоих кругов? 

Можно усложнить вопрос, добавив к подсчету фигур их признак:

- Сколько зеленых фигур лежит вне обоих кругов? 

Дети работают с двумя кругами или обручами разных цветов (синий, красный), и размера (большой, маленький) вместо пересечения двух кругов, когда можно положить маленький круг в большой. В один из кругов дети кладут картинки с неживыми предметами, в пересечении кругов находятся карточки с транспортом. Обращаю внимание детей на то, что транспорт не может быть живым, он всегда будет находиться в круге с неживыми предметами. Поэтому вместо пересечения двух кругов, можно положить маленький круг в большой.

Выполняя упражнение, дети задумываются: если все объекты первого множества входят и во второе множество, то модель будет представлять собой вложенные круги.

  Формирование умения понимать отношения между числами в пределах 5 с помощью кругов Эйлера лучше начинать рассматривать с детьми 4-5 лет, постепенно усложняя их в старшей и подготовительной к школе группе. Для наиболее способных детей существуют сложные задачи.

Метод наглядного моделирования с помощью кругов Эйлера можно использовать и в речевом развитии дошкольников. Образная, богатая синонимами, дополнениями и описаниями речь у детей дошкольного возраста – явление очень редкое. В речи детей существуют множество проблем. Поэтому педагогическое воздействие при развитии речи дошкольников – очень сложное дело. Необходимо научить детей связно, последовательно, грамматически правильно излагать свои мысли, рассказывать о различных событиях из окружающей жизни.

Дошкольники с различными речевыми нарушениями испытывают значительные трудности в усвоении, как программы дошкольного образования, так и в дальнейшем программы обучения общеобразовательной школы. Работая с детьми, педагогу приходится искать вспомогательные средства, облегчающие, систематизирующие и направляющие процесс усвоения детьми нового материала. Такими средствами являются графические модели с использованием кругов Эйлера. Элементами описательного рассказа являются качественные характеристики объекта:

- принадлежность к родовидовому понятию;

- величина;

- цвет;

- форма;

- составляющие детали;

- качество поверхности;

- материал, из которого изготовлен объект (для неживых предметов);

- как он используется (какую пользу приносит)

- за что нравится (не нравится)

Сначала ребенок составляет модель описания предметов по плану. При этом символы описания (пиктограммы) выкладываются в обручи. Затем в пересечении кругов выделяются одинаковые признаки предметов. Теперь можно составлять описательный рассказ по данной схеме, определяя сначала сходство, а затем различия предметов. Например, сравнительное описание собаки и кошки.

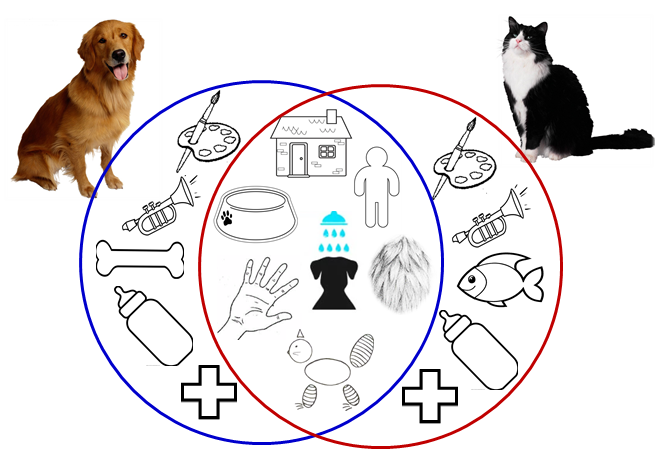
Для начала мы выделяем одинаковые признаки: «Кошка и собака – это домашние животные. О них заботится человек. Он их кормит, ухаживает за ними. Тело кошки и собаки покрыто шерстью. У этих животных есть голова, туловище, уши, хвост, лапы». Затем выделяем различия: «Кошка бело-черного цвета, а собака – рыжего. Кошка мяукает, а собака – лает. Кошка любит пить молоко, есть рыбу, а собака грызть кости. Кошка и собака приносят пользу человеку. Собака охраняет дом, а кошка ловит мышей».

Метод наглядного моделирования с помощью кругов Эйлера можно использовать при ознакомлении дошкольников с окружающим миром.

Детям предлагается набор карточек для решения задач. Например:

1. Разложить карточки так, чтобы в одном круге лежало все съедобное, а в другом – фрукты (один круг вложен в другой). Дети определяют предметы, подходящий под описания кругов. Важно обратить внимание ребенка на те, качества, которые присущи объекту всегда.

2. Разложить карточки так, чтобы в одном круге были фрукты, а другом – овощи (непересекающиеся круги). Дети определяют предметы, подходящий под описания кругов.

3. Разложить карточки так, чтобы в одном круге были все фрукты, а в другом – все красные предметы (пересекающиеся круги, в пересечении – карточка с яблоком). Сначала дети определяют предмет, подходящий под описания кругов. Каждой из пересекающихся окружностей присваивается какое-либо качество. Затем необходимо найти объект, подходящий под описание тех кругов, которые имеют общее пересечение.

Во время следующих занятий детям можно предлагать и более сложные задачи, когда в пересечении двух кругов может оказаться не одна, а несколько карточек.

Круги Эйлера очень интересный способ развития математического и логического мышления детей дошкольного возраста. Круги Эйлера – это геометрическая схема, благодаря которой можно наглядно отобразить отношения между понятиями или множествами объектов, цифр и фигур. Круги Эйлера – это схемы, которые позволяют изобразить наглядно отношения между множествами и пересечениями предметов или фигур, объединение множеств. При решении многих задач метод Эйлера просто незаменим и значительно упрощает рассуждение. Модели кругов Эйлера – просты и наглядны, поэтому они с большим успехом используются для математического развития детей дошкольного возраста, для развития логики у дошкольников. Если ребенок научится строить модели, отражающие обобщенные, существенные черты множеств объектов, он получит в свои руки инструмент, с помощью которого в дальнейшем сумеет познавать и конструировать действительность, а также самостоятельно анализировать те множества, которые перед ним. Используя круги Эйлера, дошкольникам можно продемонстрировать все варианты расположения множеств относительно друг друга. Когда ребенок учится строить модели, которые отражают обобщенные схемы объектов, то он учится таким образом познавать и конструировать действительность. Это поможет в дальнейшем детям самостоятельно выбирать оптимальное решение задач. Используя круги Эйлера, дети учатся находить объекты, обладающие сразу несколькими признаками, в отличие от остальных. У дошкольников преобладает игровая деятельность, поэтому усвоение материала лучше происходит в игровой дидактической форме, особенно хорошо такие задания выполняются в квест-играх, где необходимо решать задания, чтобы добиться нужного результата. Старшие дошкольники учатся строить довольно сложные модели с несколькими кругами, вложенными в один. С каждым разом круги можно добавлять, тем самым усложнять задания. Предлагается использование пересекающихся кругов. Такие задачи требуют от детей умения находить объекты, обладающие, в отличие от остальных, не одним, а сразу несколькими признаками. И именно с помощью пересекающихся кругов решается целый класс интереснейших логических задач в школе. Детям необходимо совершенствовать все варианты расположения множеств относительно друг друга. Это будет «взгляд сверху», который в дальнейшем даст возможность самостоятельно выбирать оптимальную для решения конкретной задачи модель. В работе с детьми использую модель положения двух, трех кругов. Такой метод развития логического мышления является актуальным, интересным и востребованным. Игры с использованием «Кругов Эйлера» хорошо воспринимают дети не только старшего, но и младшего дошкольного возраста. Такой способ математического развития детей очень эффективен и даёт положительный результат. Такие игры приобрели востребованность даже у тех детей у кого уровень развития ниже среднего. Особенно хорошо игры с Кругами Эйлера помогают при проведении мониторинга детей, где отслеживается динамика роста математического развития детей. В группе уголок математического развития должен содержать дидактические, игры с кругами Эйлера. Они должны быть доступны и понятны детям. Такие игры можно использовать как в совместной образовательной деятельности, так и предложить индивидуально ребенку. Задача образовательного процесса - не планировать общую, единую и обязательную для всех «линию», а помочь каждому ребенку, с учетом его индивидуальных способностей, развивать личную, индивидуальную траекторию. В этом случае игры с кругами Эйлера хорошо раскрывают способности и возможности каждого ребенка. Важным в таких играх является хороший подбор материала, яркое пособие и доступность в обучении. Ведь любые новые знания, а особенно математические, для детей это их личная победа. Игры должны приносить детям радость, увлеченность. Используя игры «Круги Эйлера» дети стремятся быть услышанными, не боятся ошибиться, проговаривать разные варианты решения, делать выводы. Это способствует активному выражению своей точки зрения детьми. Когда ребенок сам анализирует и находит пути решения задачи, это помогает ему увидеть, понять и исключить свои ошибки. Эти игры должны иметь в наличии большой выбор наглядного пособия, карточки, схемы, картинки, наборы цифр, геометрических фигур и др.

Используя в работе с детьми данную технологию, мы способствуем развитию у них умений анализировать объекты с целью выделения признаков, осуществлять анализ и синтез, то есть составлять целое из частей, в том числе самостоятельно достраивая множества недостающими компонентами, умений сравнивать и классифицировать, обобщать, делать выводы и умозаключения, строить логические цепочки, рассуждать. Это означает, что мы вооружаем детей необходимыми инструментами для дальнейшего успешного обучения в школе. Учиться станет легче, а значит, и процесс учебы, и сама школьная жизнь будут приносить радость и удовлетворение