Многоликая симметрия и золотое сечение

КГУ ШГ № 6

Разработка урока по курсу «Математический практикум»

Тема: «Многоликая симметрия и золотое сечение».

7 класс

.

Учитель по математике: Германцева Г.Р.

г. Алматы

Урок по курсу «Математический практикум» 7 класс

Тема: «Многоликая симметрия и золотое сечение». (2 часа)
Цели: 
1.Образовательные: Дать представление о симметрии в математике, химии, физике, биологии, Познакомить с основными видами симметрии. Показать возможности использования понятия «симметрия» при решении задач.

2.Развивающие: Активизировать самостоятельную деятельность. Развивать познавательную активность. Учить обобщать и систематизировать полученную информацию.

3.Воспитательные: Воспитывать коммуникативность. Расширить кругозор учащихся, способствовать развитию познавательного интереса. Показать школьникам общеинтеллектуальное значение математики. Способствовать познанию законов красоты и гармонии окружающего мира.

Оборудование: компьютер, видеопроектор, экран, напечатанный эпиграф урока (закреплен на доске)

ХОД УРОКА:

1. Организационный момент

2. Актуализация субъективного опыта

Тестирование: слайд-шоу на 5 минут, учащиеся должны выбрать, что привлекает их взгляд или на какой фигуре взгляд дольше задержался, ответы учащихся записать на доске

1. Изучение нового материала

1. Вступительное слово

«…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…». 
Иоганн Кеплер 
Можно ли «проверить алгеброй гармонию?» – сказал А.С. Пушкин. 

Окружающий нас мир многообразен…Вы, наверное, обращали внимание, что мы неодинаково относимся к предметам и явлениям окружающей действительности. Беспорядочность, бесформенность, несоразмерность воспринимаются нами как безобразное и производят отталкивающее впечатление. А предметы и явления, которым свойственна мера, целесообразность и гармония воспринимаются как красивое и вызывают у нас чувство восхищения, радости, поднимают настроение. (Проанализировать результаты проведенного тестирования).
Людей с давних времён волновал вопрос, подчиняются ли такие неуловимые вещи как красота и гармония, каким-либо математическим расчётам.
Сегодня на уроке познакомимся с понятиями «симметрия» и «золотое сечение». Там, где они присутствуют, ощущается гармония и красота, они вызывают у нас чувство восхищения, радости, поднимают настроение. 
2) Виды симметрии

Симметрия (от греческого symmetria - «соразмерность») - понятие, означающее сохраняемость, повторяемость, «инвариантность» каких-либо особенностей структуры изучаемого объекта при проведении с ним определенных преобразований. 
Учитель математики: идея симметрии часто является отправным пунктом в гипотезах и теориях учёных прошлых веков, веривших в математическую гармонию мироздания и видевших в этой гармонии проявление божественного начала. Древние греки считали, что Вселенная симметрична просто потому, что симметрия прекрасна. 
Простейшими видами пространственной симметрии являются центральная, осевая, зеркально- поворотная и симметрия переноса. 
Центральная симметрия (слайд 1)
Две точки А и А1 называются симметричными относительно точки О, если О - середина отрезка АА1. Точка О считается симметричной самой себе. 
 
Оевая симметрия (слайд 2)
Преобразование фигуры F в фигуру F1, при котором каждая ее точка переходит в точку, симметричную относительно данной прямой, называется преобразованием симметрии относительно прямой а. Прямая а называется осью

симметрии.

  

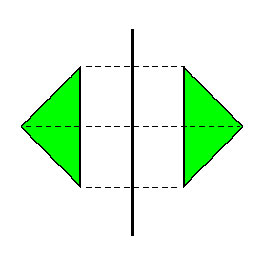
Зеркально-поворотная симметрия (слайд 3)

Если во внутрь квадрата вписать с поворотом другой квадрат, то это и будет

пример зеркально-поворотной симметрии. 

Переносная симметрия (слайд 4)
Если при переносе плоской фигуры F вдоль заданной прямой АВ на расстояние a

(или кратное этой величине) фигура совмещается сама с собой, то говорят о

переносной симметрии. Прямая АВ называется осью переноса, расстояние a

элементарным переносом или периодом.

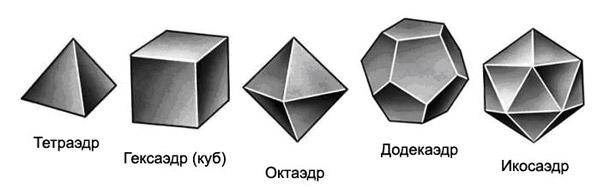
3) Симметрия многогранников

Симметрии треугольника и других геометрических тел большое значение придавали греческие мыслители эпохи Пифагора. Они считали, что для того, чтобы тело было «совершенно симметричным», оно должно иметь равное число граней, встречающихся в углах, и эти грани должны быть правильными многоугольниками, то есть фигурами с равными сторонами и углами. (слайд 5)

4) Что такое «Золотое сечение»?

Можно привести множество примеров присутствия симметрии в окружающем нас мире. Эстетическое наслаждение, получаемое человеком при наблюдении совершенных форм предмета, объясняется не только выполнением законов симметрии, но и присутствием так называемой «божественной» пропорции, «золотого сечения» в соотношении частей, на которые предмет делится естественным образом.

Сегодня на уроке мы познакомимся с этим понятием, научимся делить отрезок в золотом отношении, увидим, где оно встречается в природе, как используется в технике и произведениях искусства. Термин золотое сечение ввёл в XVI веке великий художник, учёный и изобретатель Леонардо да Винчи. В истории утвердились три варианта названия: «золотое сечение», «золотая пропорция» и третье – «деление отрезка в среднем и крайнем отношениях». Кроме того, золотое сечение награждали эпитетами «божественное», «чудесное», «превосходнейшее», потому что-то, где оно присутствует, вызывает у нас ощущение красоты и гармонии.

Что же такое золотое сечение? 
Рассмотрим отрезок АВ.  (слайд 6)

Его можно разделить точкой С на две части бесконечным множеством способов, но говорят, что точка С производит золотое сечение отрезка АВ, если выполняется пропорция: длина меньшего отрезка так относится к длине большего, как больший отрезок относится к длине всего отрезка. Приближённое значение этого числа равно 0,6. Такая пропорция и задаёт золотое сечение. Её называли божественной пропорцией.

Понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. д. н. э.). Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Рельеф из храма фараона Сети I в Абидосе и рельеф, изображающий фараона Рамзеса, соответствуют величинам золотого деления. В фасаде древнегреческого храма золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

Все живое и все красивое – все подчиняется божественному закону, имя которому – «золотое сечение». Говорят, что “божественная пропорция” заложена в природе, и во многих вещах вокруг нас. С тех пор как это соотношение было открыто, многие художники и архитекторы применяли его в своих работах. Вы можете найти золотое сечение в нескольких шедеврах эпохи Возрождения, архитектуре, живописи, и многом другом.

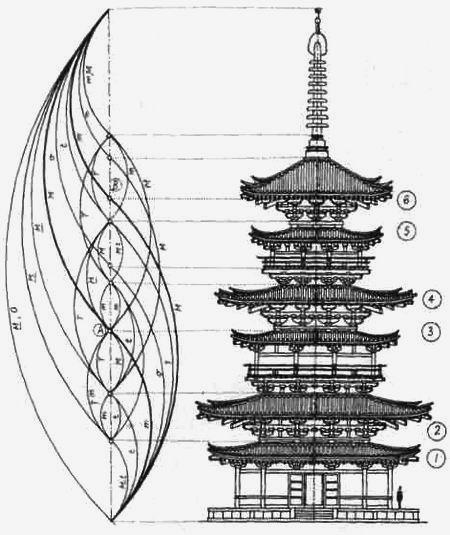
5) Золотое сечение в архитектуре

Развалины Парфенона в Афинах- одно из знаменитых сооружений в мире. Он был построен в эпоху расцвета древнегреческой культуры.

На слайде видно, каким образом фасад Парфенона вписывается в прямоугольник, стороны которого образуют золотое сечение. Длина прямоугольника больше его ширины примерно в 1,618 раз.Все архитектурные сооружения, храмы и даже жилища от Древнего Египта и Древней Греции до наших дней создавались и создаются в гармонии чисел по правилам Золотого сечения. (слайд 7)

6) Золотое сечение человеческого тела

Художник Альбрехт Дюрер установил, что рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица — ртом и т.д. Талия делит совершенное человеческое тело в отношении золотого сечения. Таковы, например, знаменитые статуи Аполлона Бельведерского работы Леохора и Зевса Олимпийского ваятеля Фидия. Пропорции мужского тела колеблются в пределах среднего отношения и несколько ближе подходят к золотому сечению, чем пропорции тела женщин. (слайд 8)

Золотое сечение раскрыло далеко не все свои тайны. Совсем недавно его нашли, к примеру, в медицине и физиологии. Скажем, установлено, что для каждого вида живых существ есть частота сердцебиений, при которой длительность всего кардиоцикла и его составляющих соотносятся между собою по пропорции золотого сечения. Для человека эта частота равна сердечному ритму здоровых, физически активных организмов в покое: почти 63 удара в минуту. Эта пропорция “присутствует” и в сосудах, и в крови. Словом, золотое сечение является гарантом нормального, оптимального функционирования всей кровеносной системы организма.

7) Золотое сечение в растительном мире

Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение). Рассматривая расположение листьев на общем стебле растений можно заметить, что между каждыми двумя парами листьев А и С третье расположение в месте золотого сечения точка В. Длина лепестков тоже подчинена золотой пропорции. (слайд 9).

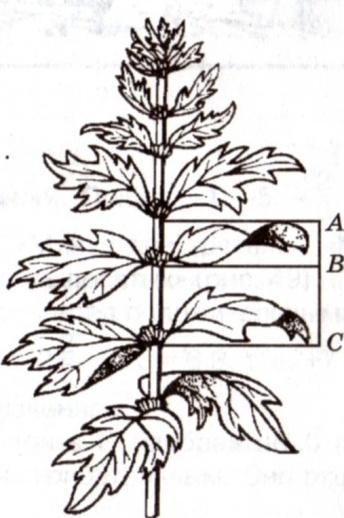
8) Золотое сечение в животном мире

И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы – симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста. Природа осуществила деление на симметричные части и золотые пропорции. Несколько примеров. В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38. (слайд 10)

9) Золотое сечение в живописи

Переходя к примерам «золотого сечения», нельзя не остановить своего внимания на творчестве Леонардо да Винчи. (слайд 11). Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка построена на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника.

10) Золотое сечение в литературе

Многое в структуре поэтических произведений роднит этот вид искусства с музыкой. Четкий ритм, закономерное чередование ударных и безударных слогов, упорядоченная размерность стихотворений, их эмоциональная насыщенность делают поэзию родной сестрой музыкальных произведений. Каждый стих обладает своей музыкальной формой - своей ритмикой и мелодией. Можно ожидать, что в строении стихотворений проявятся некоторые черты музыкальных произведений, закономерности музыкальной гармонии, а, следовательно, и золотая пропорция.  Представляет несомненный интерес анализ романа "Евгений Онегин" А.С.Пушкина. Этот роман состоит из 8 глав, в каждой из них в среднем около 50 стихов. Наиболее совершенной, наиболее отточенной и эмоционально насыщенной является восьмая глава. В ней 51 стих. Кульминацией главы является объяснение Евгения в любви к Татьяне - строка "Бледнеть и гаснуть ... вот блаженство!". Эта строка делит всю восьмую главу на две части - в первой 477 строк, а во второй - 295 строк. Их отношение равно 1,617! Тончайшее соответствие величине золотой пропорции! Это великое чудо гармонии, совершенное гением Пушкина! 

11) Золотое сечение в дизайне

  

С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и другие сферы.

Неудивительно, что вы также можете найти использование золотого сечения во многих современных проектах, в частности, дизайне. Это может быть использовано в дизайне логотипа. Рассмотрим некоторые из самых известных в мире брендов, которые использовали золотое сечение для совершенствования своих логотипов. (слайд 12)

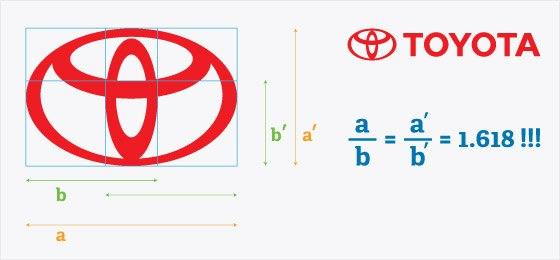
  Закрепление знаний. 
1.Назовите примеры различных видов симметрии.

2. Начертите окружность и определите, как проходит ось симметрии. Сколько осей симметрии

имеет окружность?

3. Начертите квадрат, прямоугольник, равнобедренный и равносторонний треугольник.

Имеют ли эти фигуры ось симметрии и сколько осей? 

4. Какие из следующих букв имеют центр симметрии?

5. Какие из следующих букв имеют ось симметрии?

6.Когда говорят, что некоторая точка произвела золотое сечение отрезка?

7. Выполнение тестовой работы в 2 вариантах.
V. Итоги урока
VI. Домашняя работа.
1. Подготовить презентацию на тему: «Симметрия в природе», «Золотое сечение»

2. Произвольный отрезок разделите в золотом отношении.
VII. Рефлексия