Просмотр содержимого документа
«Множества. Операции над множествами. Доклад»
ФГБОУ ВПО САХАЛИНСКИЙ ГОСУДВРСТВЕННЫЙ УНИВЕРСИТЕТ
ЮЖНО-САХАЛИНСКИЙ ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ
Кафедра математики
и информатики
Доклад:
«Множества. Операции над множествами»
Бурлакова Татьяна Евгеньевна
специальность 050146.52
преподавание
в начальных классах
курс 2,группа 112
Челнокова Ирина Андреевна.
Южно-Сахалинск
2012г.
Множество - это совокупность, набор элементов, объединенных общими свойствами.
Множества обозначаются заглавными латинскими буквами 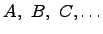 , а элементы множества строчными латинскими буквами
, а элементы множества строчными латинскими буквами 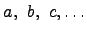 .
.
Запись 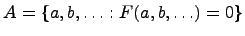 означает, что есть множество
означает, что есть множество  с элементами
с элементами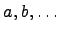 , которые связаны между собой какой-то функцией
, которые связаны между собой какой-то функцией 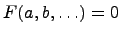 .
.
Замечание. Элементы в множество входят по одному разу, т.е. без повторений.
Основные операции:
Принадлежность элемента множеству:
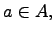
где 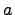 -- элемент и
-- элемент и  -- множество (элемент
-- множество (элемент 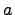 принадлежит множеству
принадлежит множеству  ).
).
Непринадлежность элемента множеству:
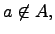
где 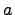 -- элемент и
-- элемент и  -- множество (элемент
-- множество (элемент 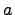 не принадлежит множеству
не принадлежит множеству  ).
).
Объединение множеств: 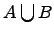 .
.
Объединением двух множеств  и
и 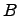 называется множество
называется множество 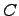 , которое состоит из элементов множеств
, которое состоит из элементов множеств  и
и 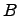 , т.е.
, т.е.
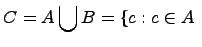 или
или
Пересечение множеств: 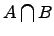 .
.
Пересечением двух множеств  и
и 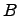 называется множество
называется множество 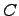 , которое состоит из общих элементов множеств
, которое состоит из общих элементов множеств  и
и 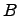 , т.е.
, т.е.
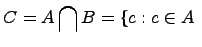 и
и
Разность множеств: 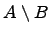 .
.
Разностью двух множеств  и
и 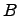 , например, множество
, например, множество  минус множество
минус множество 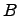 , называется множество
, называется множество 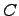 , которое состоит из элементов множества
, которое состоит из элементов множества  , которых нет в множестве
, которых нет в множестве 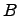 , т.е.
, т.е.
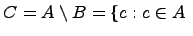 и
и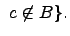
Симметрическая разность множеств: 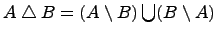 .
.
Симметрической разностью двух множеств  и
и 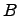 называется множество
называется множество 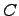 , которое состоит из не общих элементов множеств
, которое состоит из не общих элементов множеств  и
и 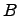 , т.е.
, т.е.
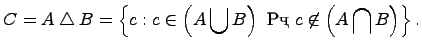
Дополнение множества: 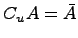 .
.
Если предположим, что множество  является подмножеством некоторого универсального множества
является подмножеством некоторого универсального множества 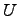 , тогда определяется операция дополнения:
, тогда определяется операция дополнения:
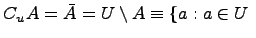 и
и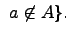
Вхождение одного множества в другое множество: 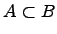 .
.
Если любой элемент множества  является элементом множества
является элементом множества 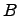 , то говорят, что множество
, то говорят, что множество  есть подмножество множества
есть подмножество множества 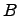 (множество
(множество  входит в множество
входит в множество 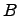 ).
).
Не вхождение одного множества в другое множество: 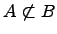 .
.
Если существует элемент множества  , который не является элементом множества
, который не является элементом множества 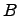 , то говорят, что множество
, то говорят, что множество  не подмножество множества
не подмножество множества 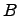 (множество
(множество  не входит в множество
не входит в множество 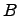 ).
).