Модульдік те?деулерді шешу ?дістері

Модульдік теңдеулерді шешу әдістері

Математика – әлемнің формуласы. Өмірдің өзі теңдеу мен теңсіздіктерден, белгісіз айнымалылардан тұрады. Мектеп математика курсында қарастырылатын теңдеулер көп емес. Солардың арасында модульдік теңдеулер аса зерттелмейді. Бірақ осы тақырыптағы есептер ҰБТ тапсырмаларында кездеседі. Модулдік теңдеулерді шешу әдістерін қарастырайық.

Мысал: 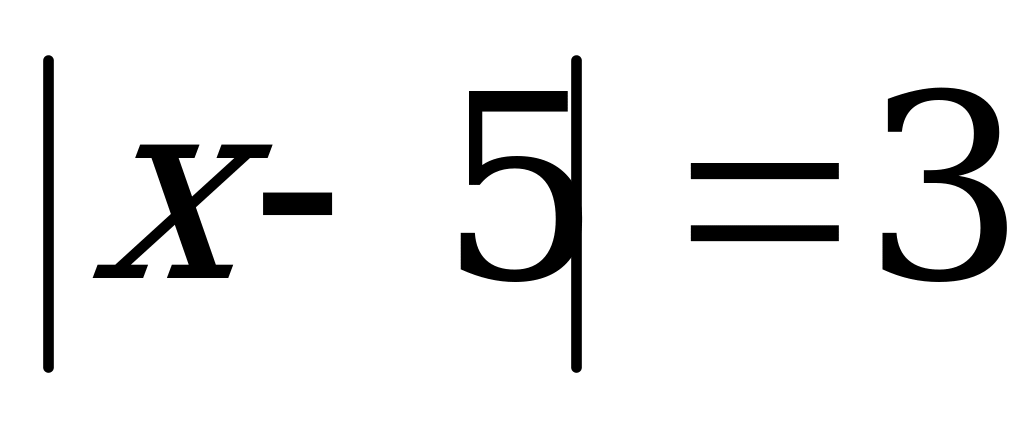теңдеуінің түбірлерін табу керек.

Шешуі:

1-әдіс. (модульдің геомериялық мағынасын пайдалану)

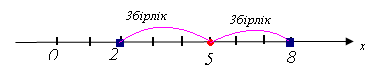
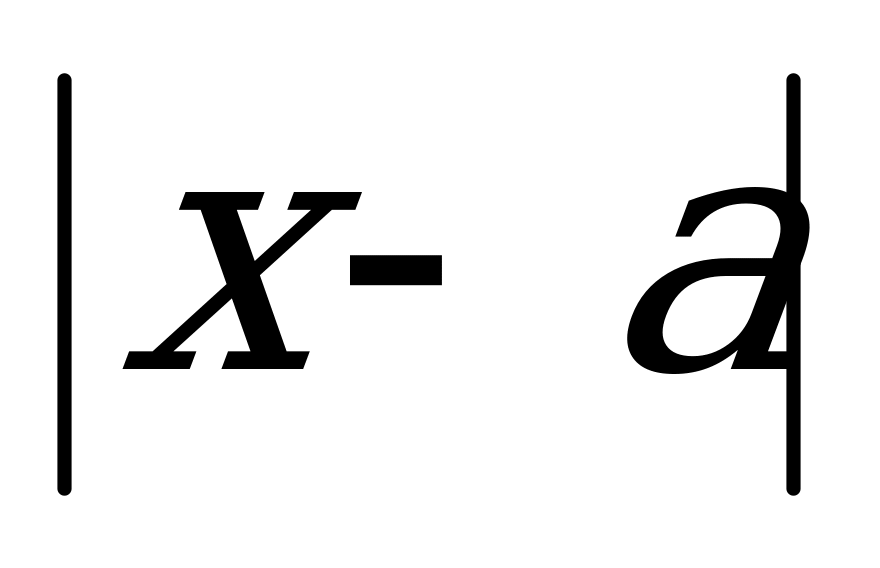өрнегінің геметриялық мағынасы – ол сан осіндегі 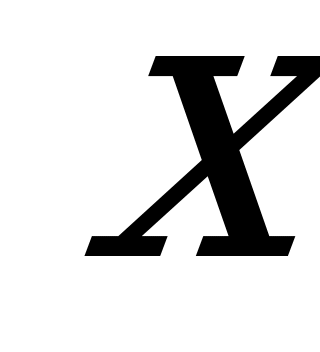нүктесінен 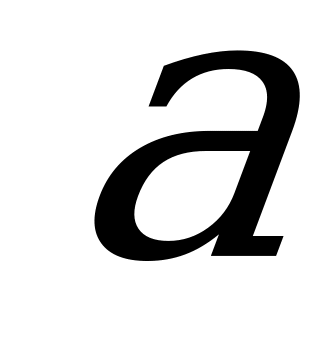нүктесіне дейінгі қашықтықты білдіреді . Онда 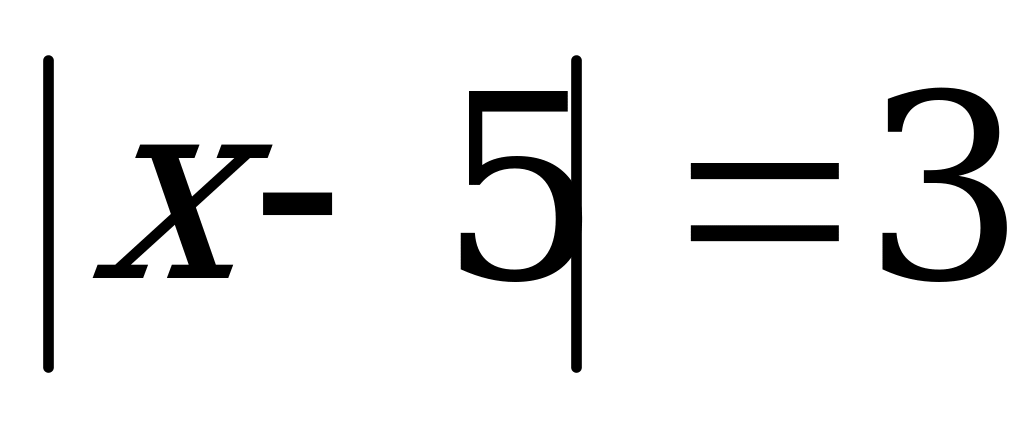теңдеуінің геометриялық мағынасы 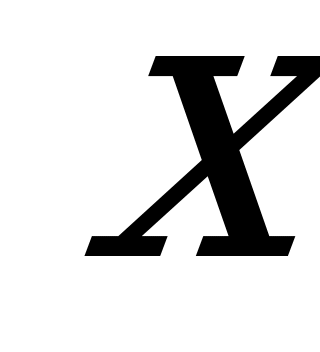және 5 нүктелерінің ара қашықтығы 3-ке тең болатындығында. Олай болса, 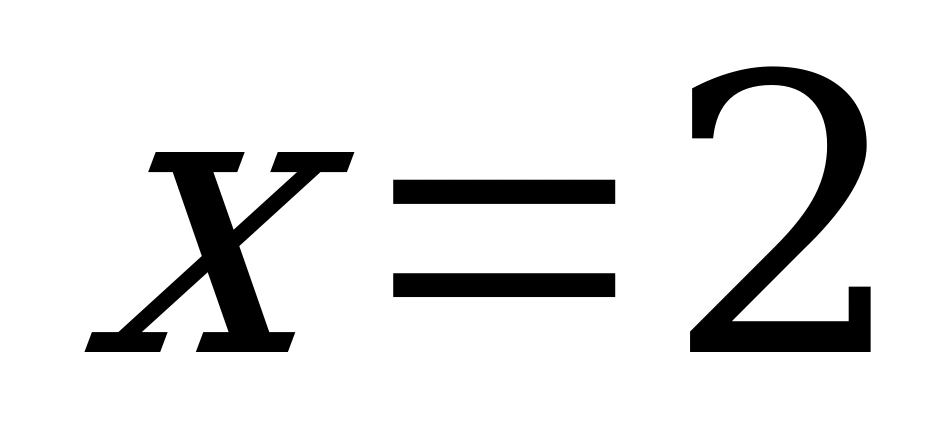және 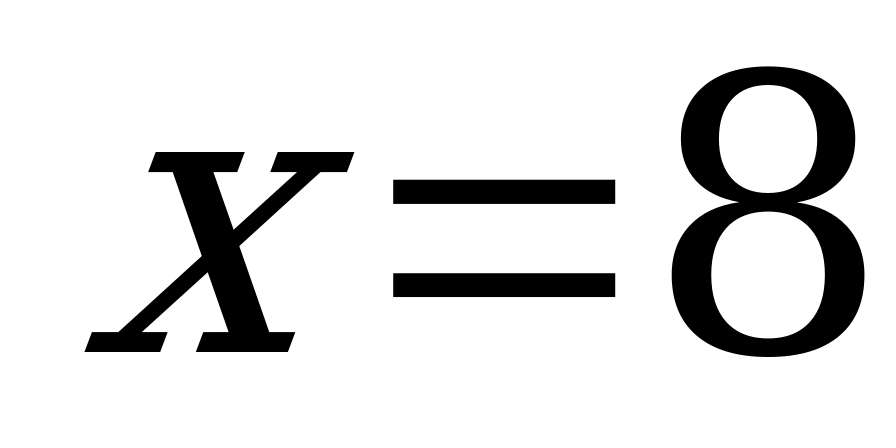болуы керек.

Жауабы: ;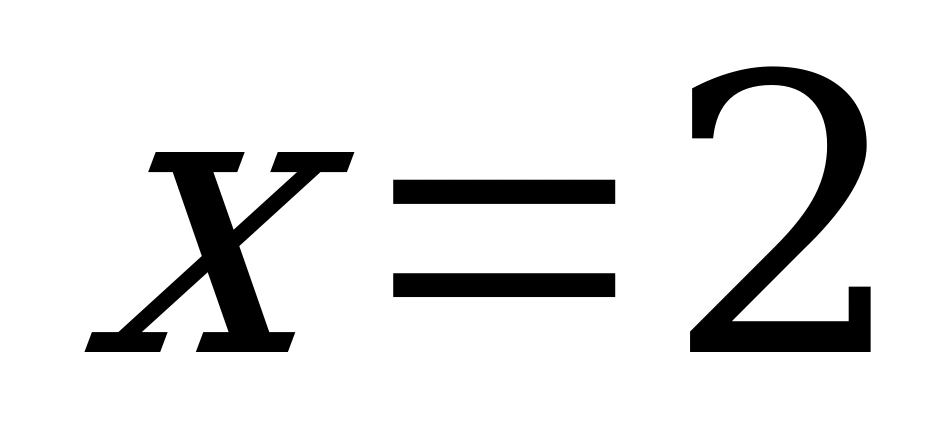

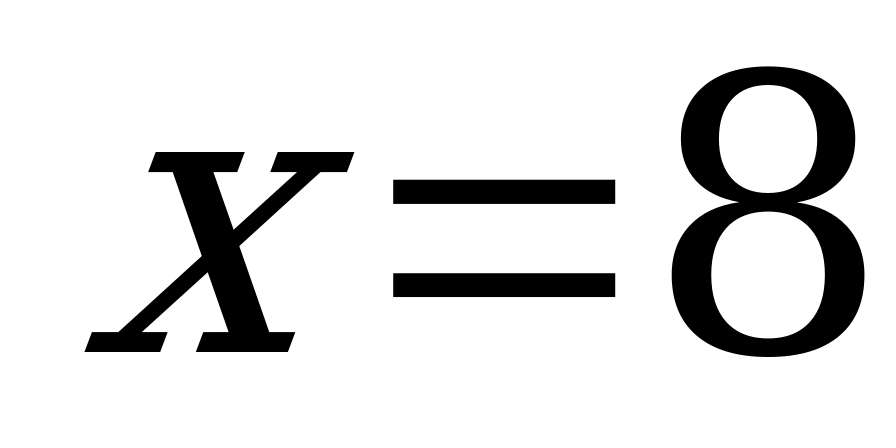
2-әдіс. (Анықтама бойынша модульді ашу). Анықтама бойынша

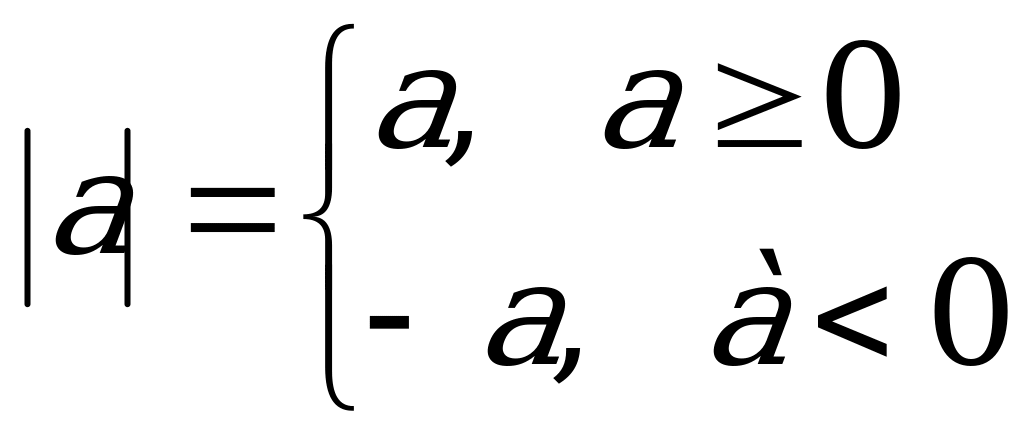
осыдан, егер 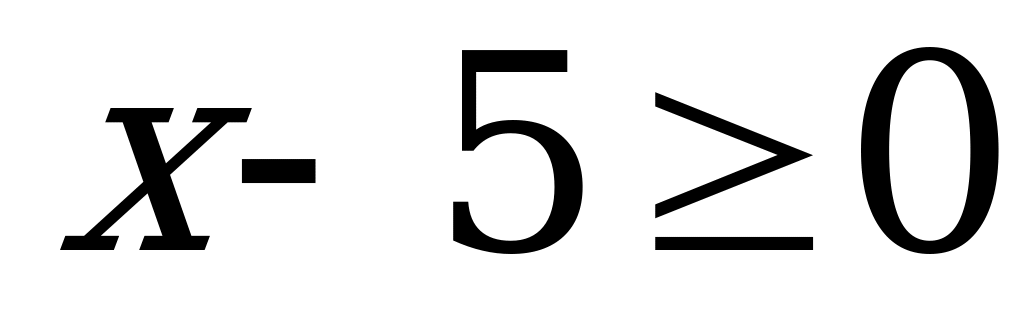болса, онда 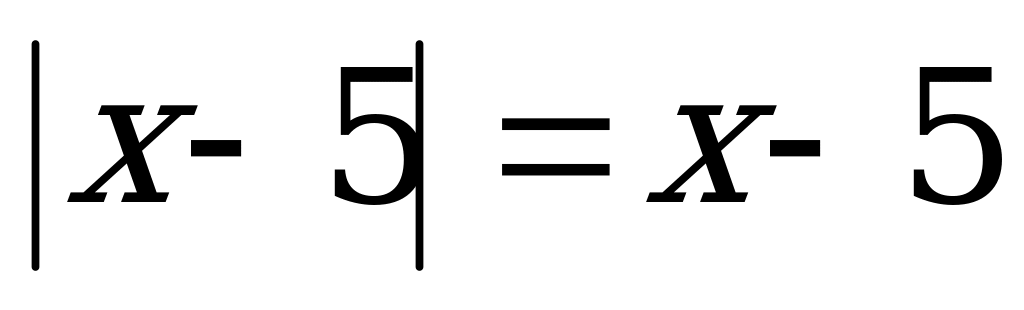теңдігі орындалады. Олай болса, 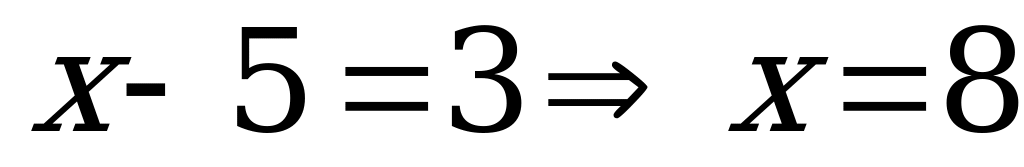. Егер 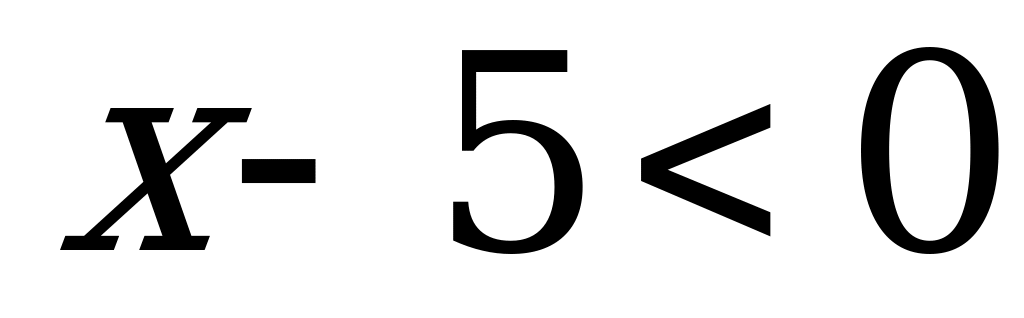болса, онда 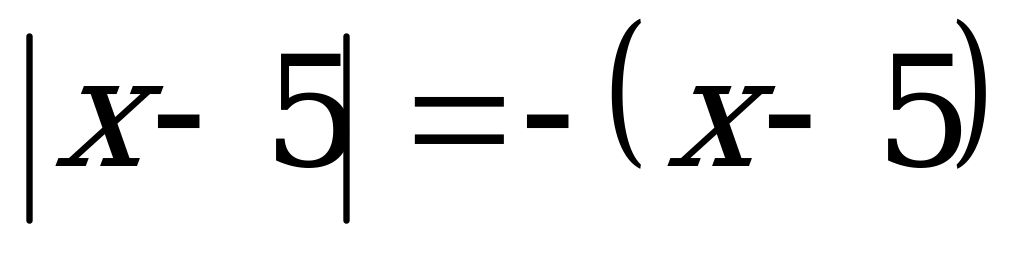теңдігі орындалады. Бұдан 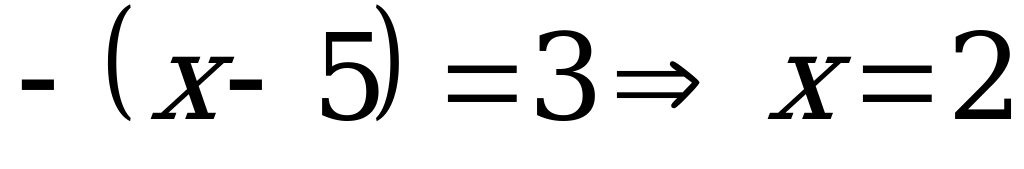. Берілген теңдеудің түбірлері 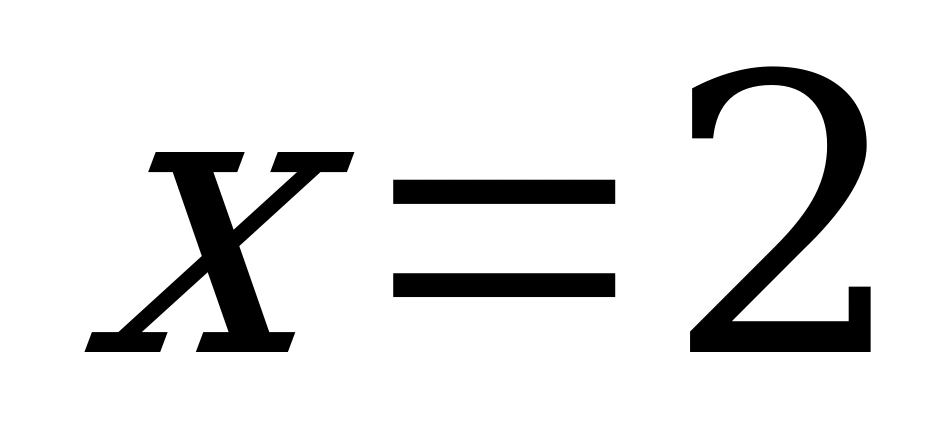және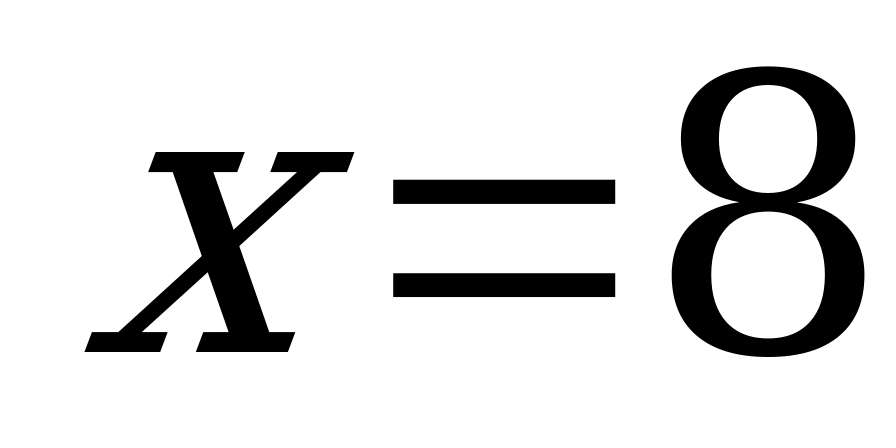

3-әдіс.(теңдеудің екі жақ бөлігін дәрежелеу) Берілген теңдеудің екі жақ бөлігі де оң болғандықтан, оны квадраттап, 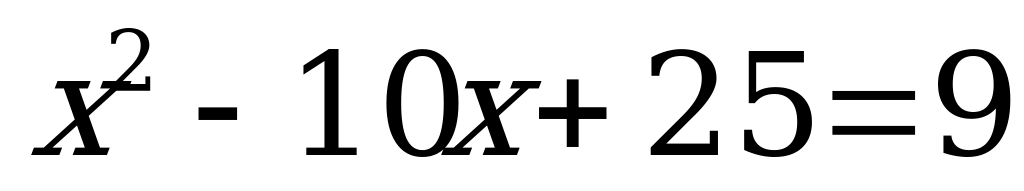немесе 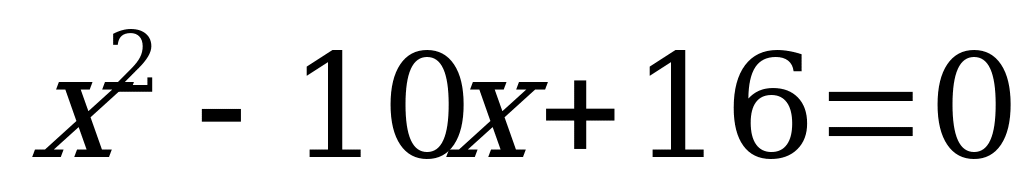квадрат теңдеуін аламыз. Бұл квадрат теңдеудің түбірлері: 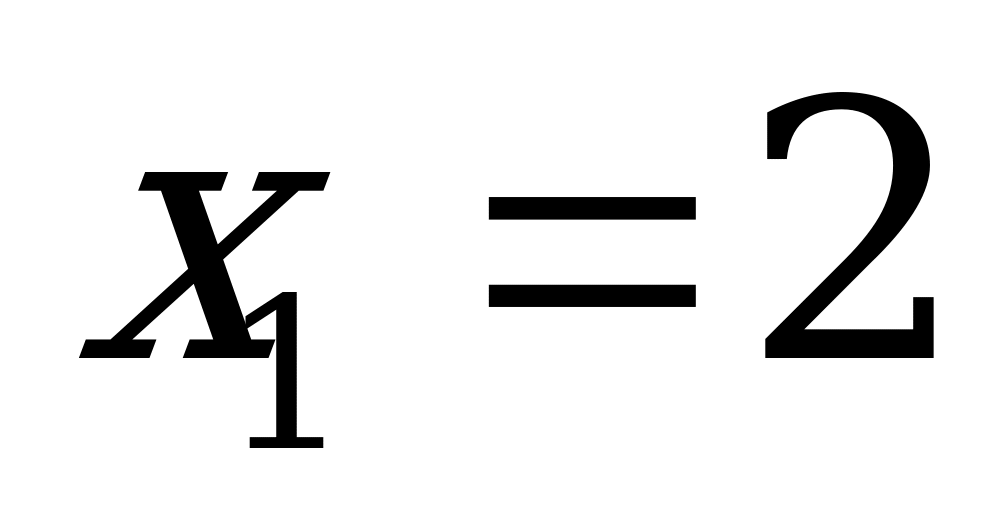және 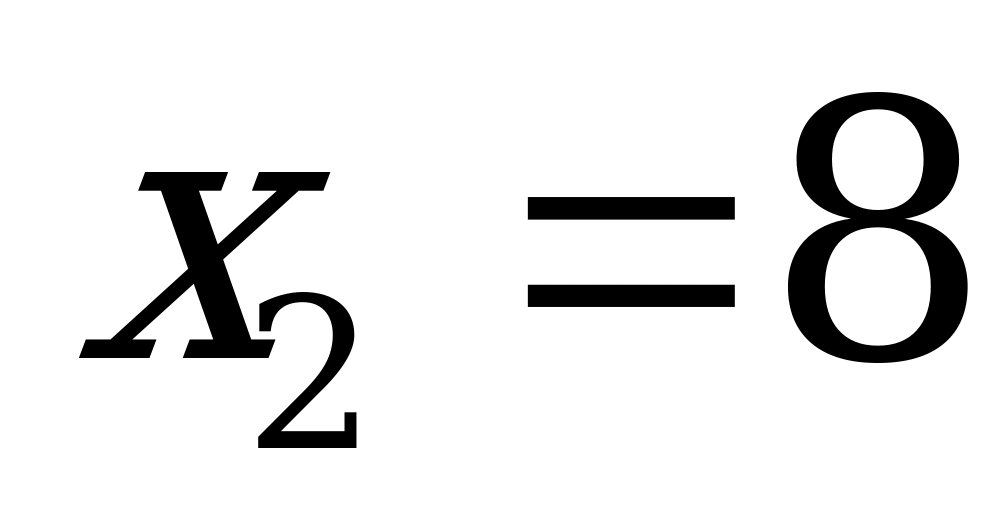. Бұлар берілген есептің жауаптары.

4-әдіс.(аралықтарға бөлу әдісі) Бұл әдісті қолданғанда модуль таңбасы астындағы екімүшелерді нөлге теңестіріп, теңдеудің түбірі анықталады. 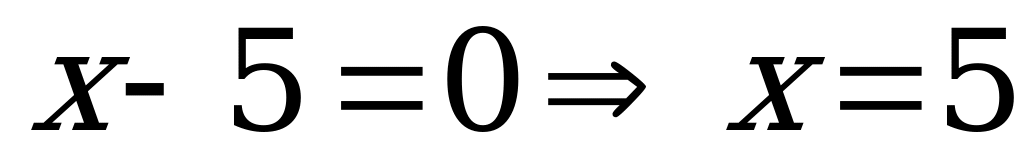табылған нүкте сан осін екі бөлікке бөледі.

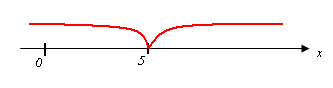
1)егер 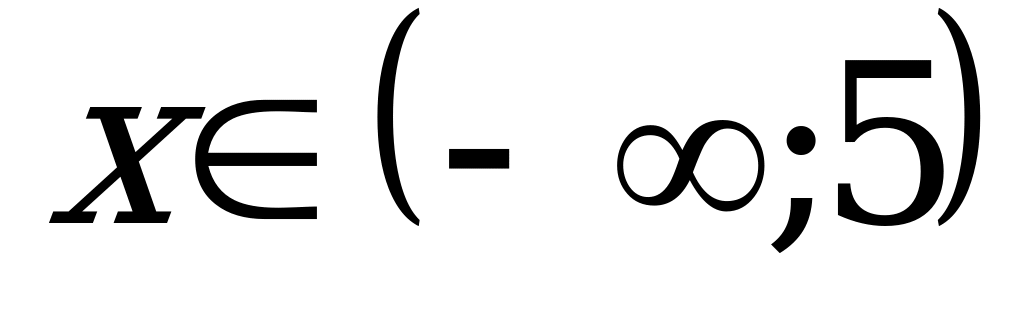болса, онда 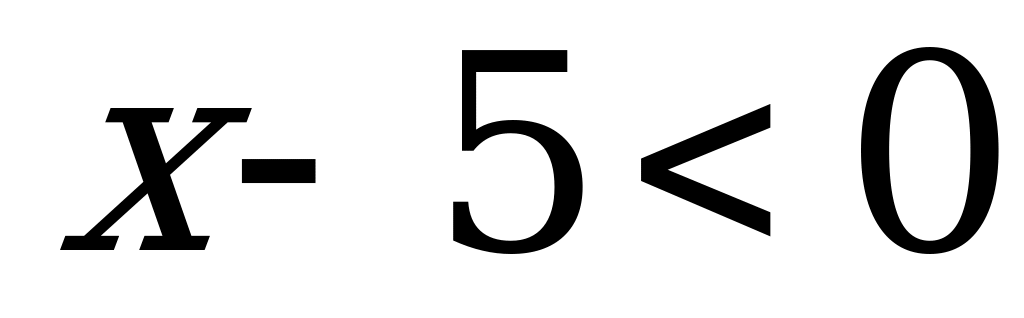. Сондықтан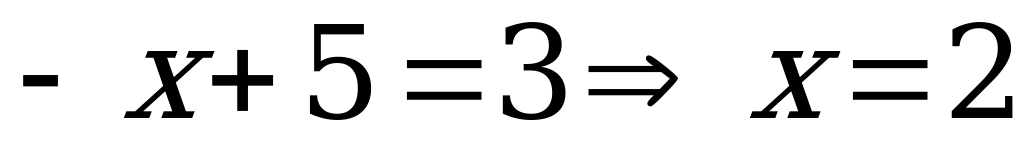

2)егер 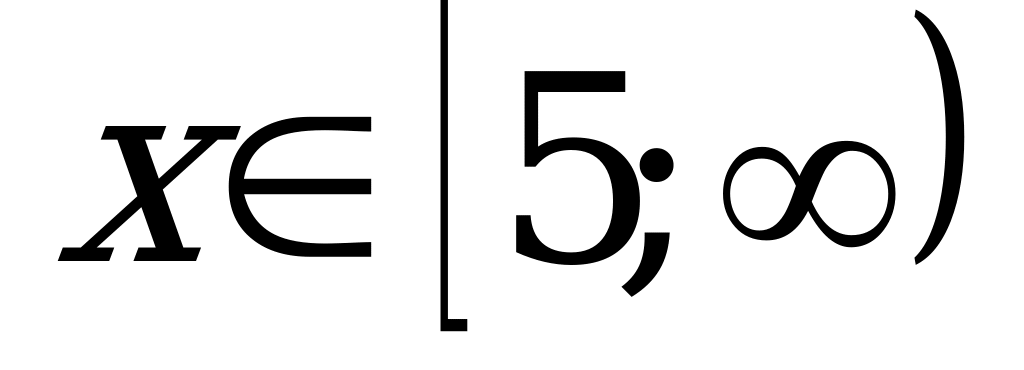болса, онда 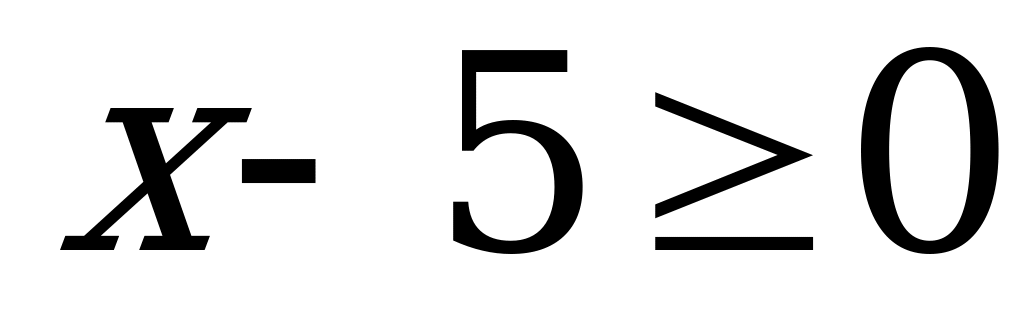. Сондықтан .

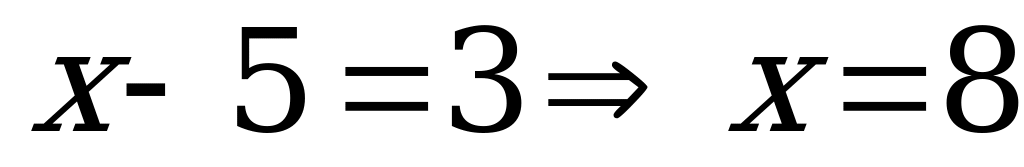5-әдіс.(графикалық әдіс)

Алдымен 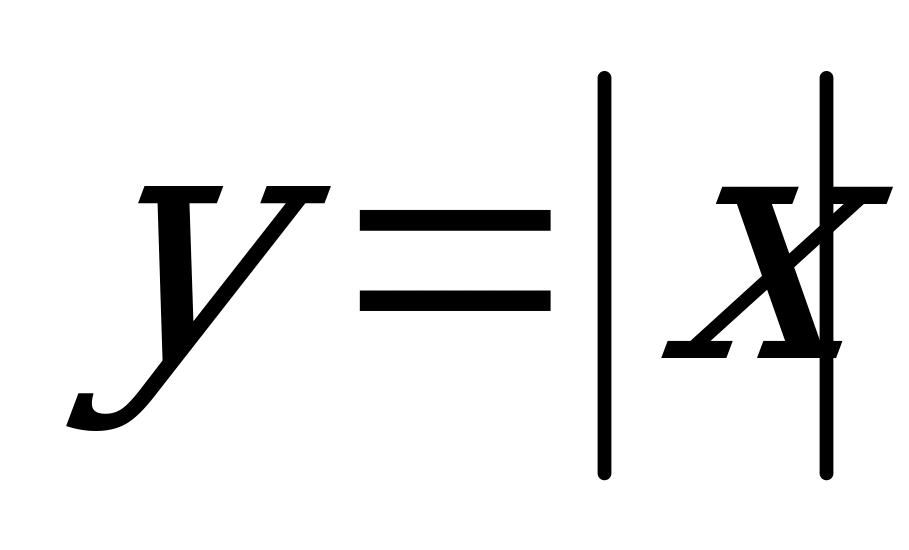функциясының графигін сызамыз. Содан кейін графикті 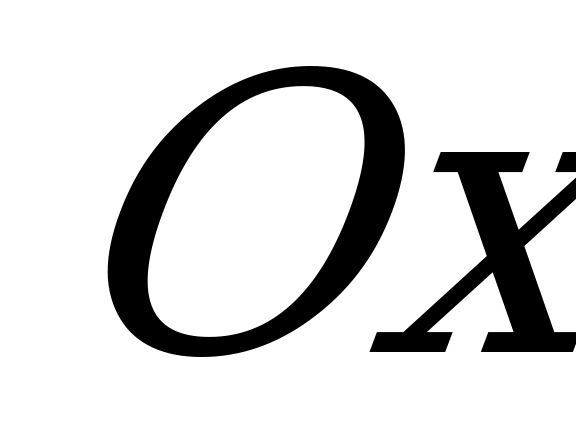осі бойымен 5 бірлік оңға жылжытамыз да 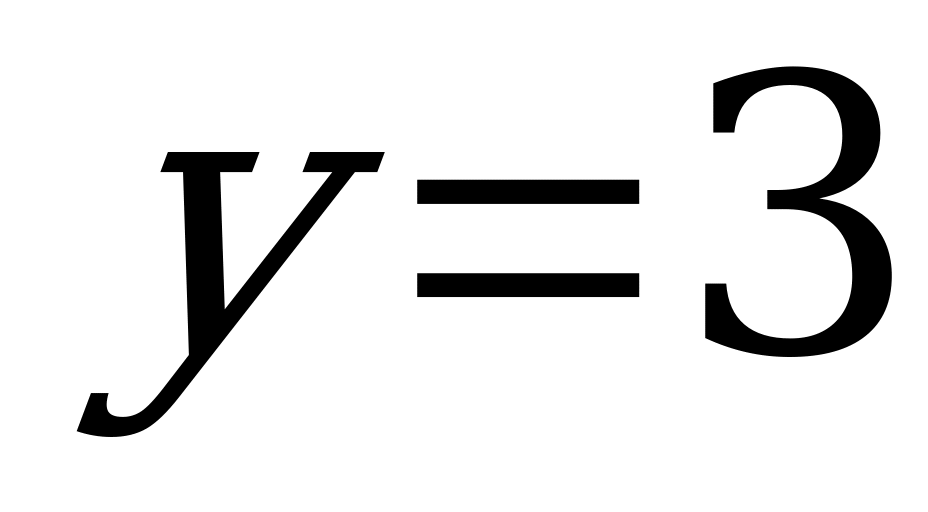функциясының графигімен қиылыстырамыз. Екі функцияның қиылысу нүктесі теңдеудің шешімі болады.

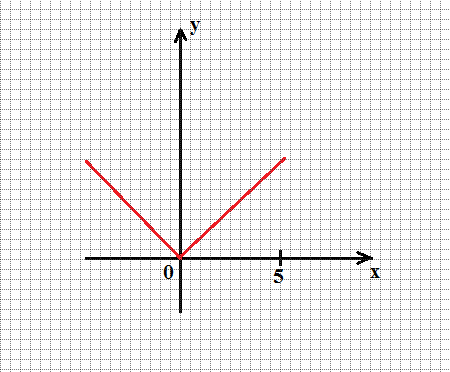
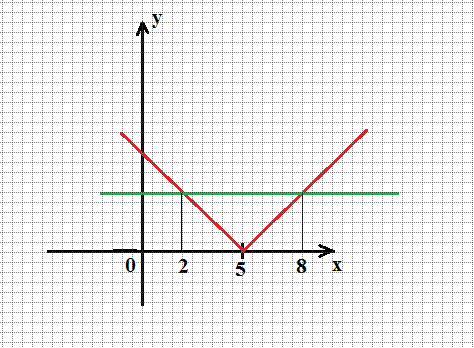
Функция графиктері 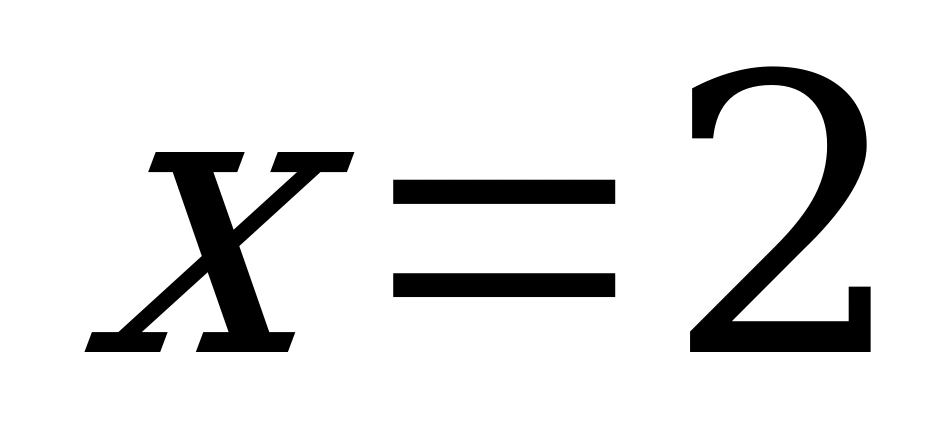және 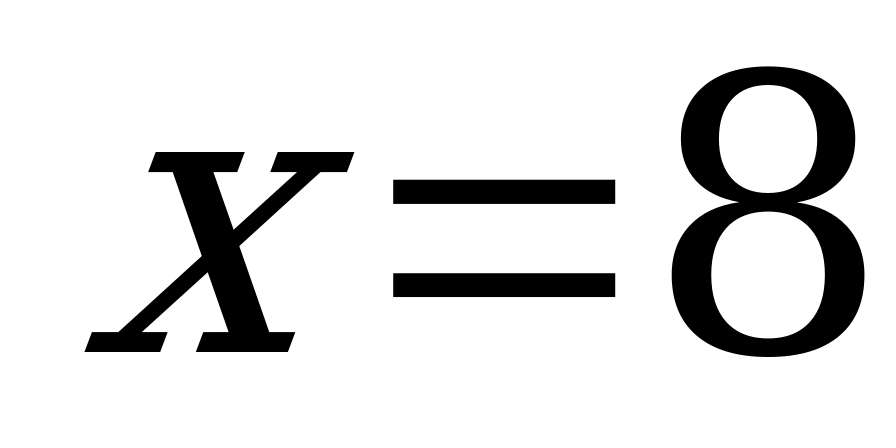нүктелерінде қиылысады. Демек, теңдеудің түбірлері 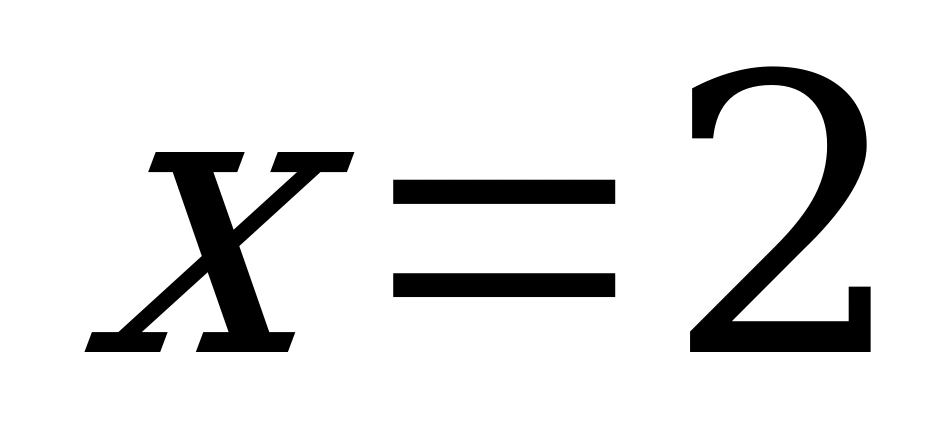және .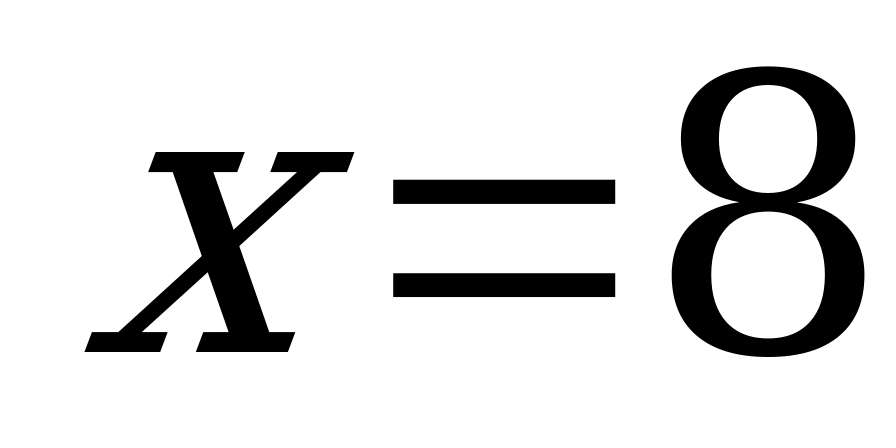

Сонымен, модульдік теңдеулерді шешудің негізгі 5 әдісін қарастырдық.