ТЕМА Накрест лежащие, соответственные и односторонние углы, образованные при пересечении параллельных прямых секущей
Цели:
систематизировать, проверить и оценить знания обучающихся по изученной теме;
формировать умения и навыки применения теоретических знаний при решении задач;
учить проводить доказательные рассуждения;
Задачи
Образовательные:
проверить умения и навыки учащихся применять свойства и признаки параллельности прямых при решении задач;
Развивающие:
развивать познавательную и творческую деятельность учащихся;
развивать умение самостоятельно добывать знания;
Воспитательные:
умение вести правильно диалог: слушать чужое мнение, предлагать собственное, вести дискуссию, корректно по отношению к другим отстаивать свою точку зрения, принимать чужую;
воспитывать аккуратность построений геометрических рисунков
УУД
Личностные УУД: формирование положительного отношения к уроку, самоопределение;
Регулятивные УУД: планировать деятельность, работать по плану;
Коммуникативные УУД: умение оформлять свои мысли в устной форме;
Познавательные УУД: анализировать, доказывать, сравнивать;
Планируемые результаты
Предметные:
Знать: определение параллельных прямых; признаки параллельных прямых; теоремы об углах, образованных параллельными прямыми и секущей;
Уметь: анализируя имеющиеся знания переходить на более высокий уровень владения материалом.
Метапредметные:
выработка умений работать с учебной информацией;
готовность к сотрудничеству с одноклассниками;
Основные понятия Параллельные прямые, секущая; соответственные углы, накрест лежащие углы, односторонние углы; свойства и признаки параллельных прямых.
Тип урока: Урок систематизации материала по данной теме.
Организационные формы общения: Индивидуальная, коллективная.
Ход урока
1. Мотивационная беседа с обучающимися.
- Здравствуйте, ребята. Сегодняшний урок мы начнём с отрывка стихотворения:
«Эти линии все знают.
Направление храня,
Они дружно убегают
В бесконечность от меня.
Мы частенько их встречаем,
Невозможно все назвать:
Пара рельсов у трамвая,
В нотоносце целых пять...»
Н.К. Шабалина
- О каких линиях идет речь в этом стихотворении?
- О параллельных линиях.
- Верно! Сегодня мы продолжаем работать по теме “Параллельные прямые”. Давайте повторим основные понятия и положения темы.
2. Фронтальная работа с классом.
- А какие прямые мы называем параллельными? (непересекающиеся прямые на плоскости называются параллельными).
- Пусть а и в — две прямые (см. рисунок 1). Тогда прямая с является секущей для прямых а и в.
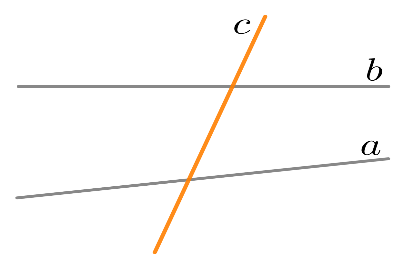 Рис. 1
Рис. 1
У углов, которые образуют прямые а и в и секущая с, есть специальные названия (см. рисунок 2).
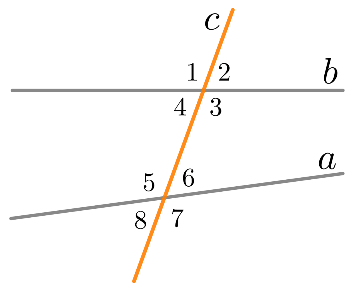 Определение Углы 3 и 5; 4 и 6 называются накрест лежащие.
Определение Углы 3 и 5; 4 и 6 называются накрест лежащие.
Углы 4 и 5; 3 и 6 называются односторонние.
Углы 1 и 5; 4 и 8; 2 и 6; 3 и 7 называются соответственные.
-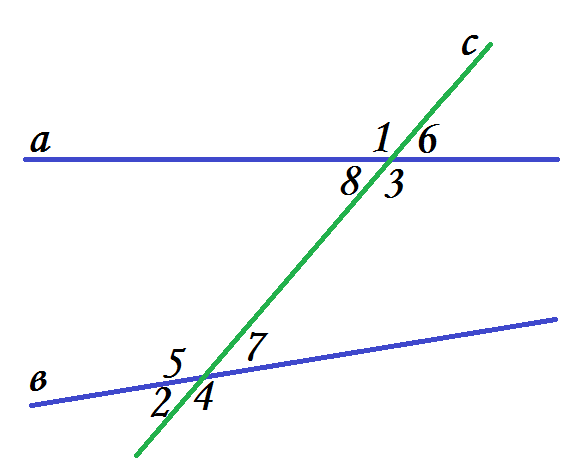 Выберите верные утверждения.
Выберите верные утверждения.
1 и 3 – вертикальные;
5 и 1 – односторонние;
6 и 7 – соответственные;
4 и 2 – смежные;
1 и 7 – накрест лежащие;
7 и 3 – односторонние .
- Какой факт о параллельных прямых вы знаете? (Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной). Как этот факт называется? (аксиомой параллельных прямых).
- Какие следствия вытекают из этой аксиомы? (Если прямая пересекает одну из параллельных прямых, то она пересекает и вторую. Если две прямые параллельны третьей прямой, то они параллельны).
- Сформулируйте I признак параллельности прямых. (Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны).
Как мы выяснили на прошлом уроке, прямая, пересекающая данную прямую, пересечет также прямую, параллельную данной. Это следствие из аксиомы параллельности открывает нам возможность сформулировать конкретные признаки параллельности прямых, по которым можно доказательно заключать о параллельности тех или иных прямых. Вы все правильно поняли: от аксиом мы наконец переходим к теоремам.
Теорема 1. Признак параллельности двух прямых
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Доказательство: Пусть прямые и образуют с секущей равные накрест лежащие углы (см. рисунок 3).
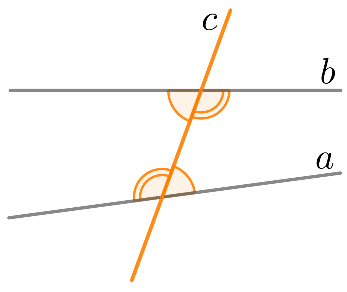 Рис. 3
Рис. 3
Допустим, прямые а и в не параллельны, а значит, пересекаются в некоторой точке С.
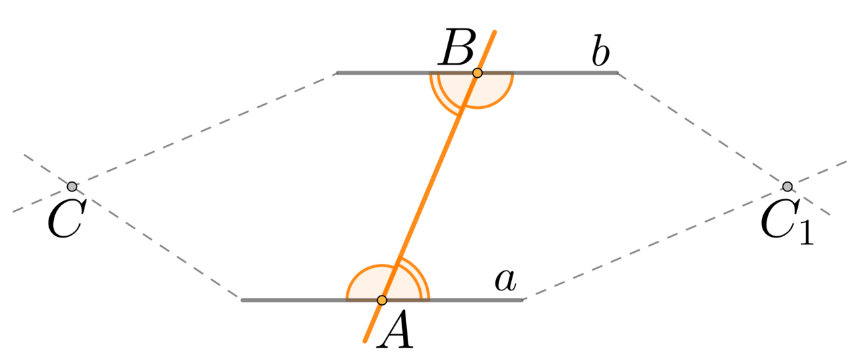
Рис. 4
Секущая с разбивает плоскость на две полуплоскости. В одной из них лежит точка С. Пусть секущая с пересекает прямую а в точке А, а прямую в — в точке В. Построим треугольник ВАС1, равный треугольнику АВС, с вершиной С1 в другой полуплоскости. Такой треугольник существует по аксиоме существования треугольника, равного данному. Так как соответствующие углы треугольников АВС и АВС1 с вершинами А и В равны, то, по аксиоме откладывания углов, они совпадают с внутренними накрест лежащими углами. Значит, прямая АС1 совпадает с прямой а, а прямая ВС1 совпадает с прямой в. Следовательно, через точки С и С1 проходят две различные прямые а и в, что противоречит аксиоме принадлежности точек и прямых. Значит, прямые а и в параллельны.
Теорема 2. Признак параллельности двух прямых
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Доказательство: Пусть прямые и образуют с секущей равные соответственные углы: (см. рисунок 5).
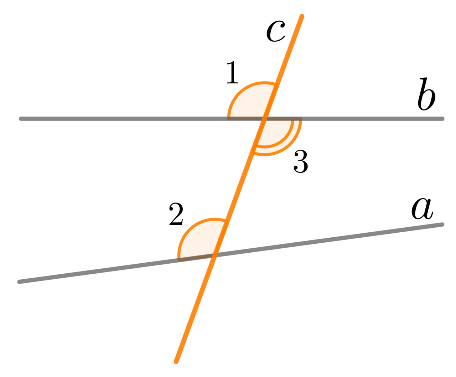 Рис. 5
Рис. 5

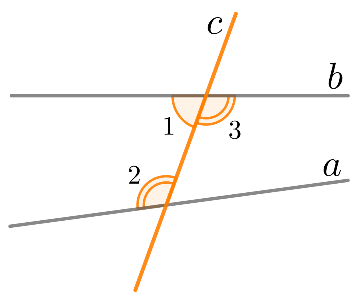
Теорема 3. Признак параллельности двух прямых
Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.


- Сколько таких признаков существует? (3). Какие это признаки? (по равенству накрест лежащих углов, по равенству соответственных углов, по сумме односторонних углов).
- Сформулируйте I признак параллельности прямых. (Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны).
- Сформулируйте II признак параллельности прямых. (Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны).
- Сформулируйте III признак параллельности прямых. (Если при пересечении двух прямых секущей сумма односторонних углов равна 180о, то прямые параллельны).
Пример. По данным рисунка докажите, что 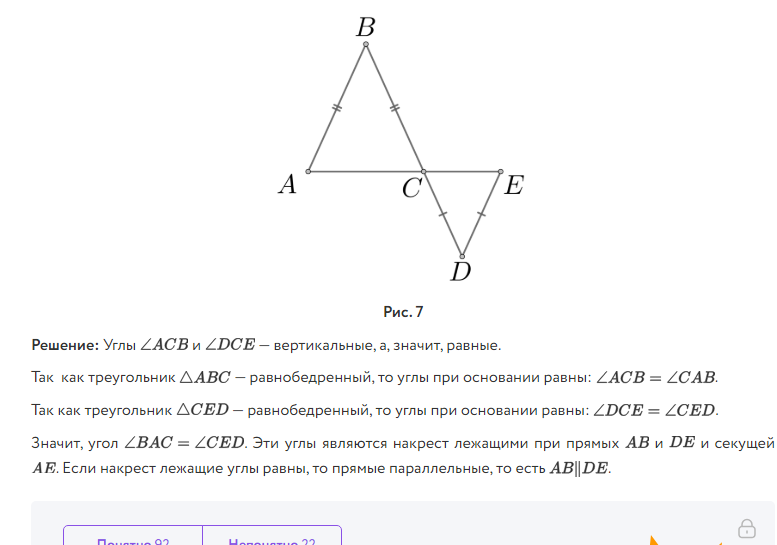

3. Решение задач по готовым чертежам.
- Молодцы. А теперь будьте внимательны. Какой вопрос перед нами? Внимание на чертеж.
З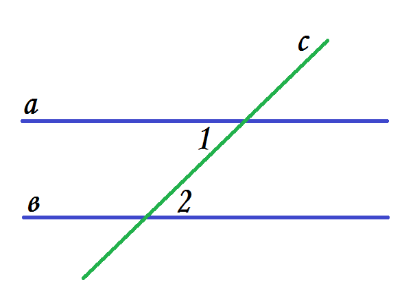 адача 1. Дано:
адача 1. Дано: 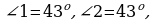 Доказать, что aǁb.
Доказать, что aǁb.
- Что нам надо доказать? (aǁb) .
- С помощью чего мы это будем доказывать? (с помощью признака параллельности прямых).
- Какой признак мы можем здесь использовать? (по равенству накрест лежащих углов).
- Докажите, что прямые параллельны. (т.к. 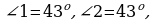 то
то 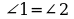 , а они накрест лежащие при прямых a и b и секущей с , значит прямые параллельны по равенству накрест лежащих углов. ч.т.д.)
, а они накрест лежащие при прямых a и b и секущей с , значит прямые параллельны по равенству накрест лежащих углов. ч.т.д.)
На основании чего прямые параллельны? Аналогично решаются следующие задачи.

Дано: 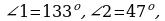 Доказать, что aǁb.
Доказать, что aǁb.
З 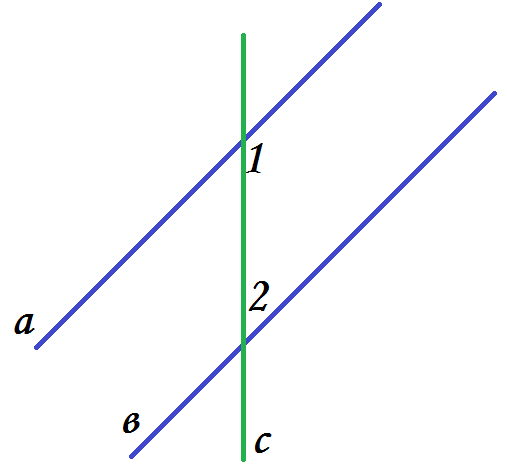
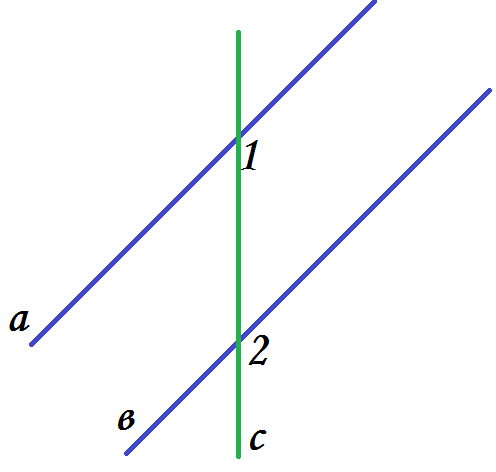 адача 2. Задача 3.
адача 2. Задача 3.

Дано: 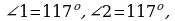 Доказать, что aǁb.
Доказать, что aǁb.
Физминутка
З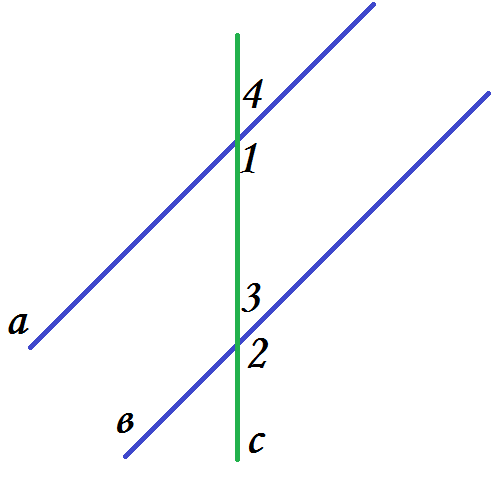 адача 4.
адача 4.

Дано: 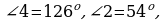 Доказать, что aǁb.
Доказать, что aǁb.

3=4
3=6
3+5=1800
1=2=900
3=5
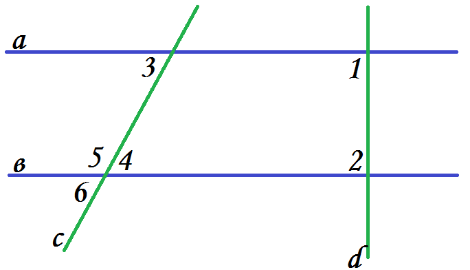
- Ответьте на вопрос, параллельны ли прямые
а и
b, если:
- Ответы пишем в тетради и сдаем работы.
- Проверяем. Поднимите руки кто правильно ответил на все вопросы; кто какие ошибки допустил? (для объяснения ошибок).
- Молодцы. К доске идут работать 2 ученика (по карточкам). А мы будем работать на местах.
- Записываем в тетрадях: Задача 5.
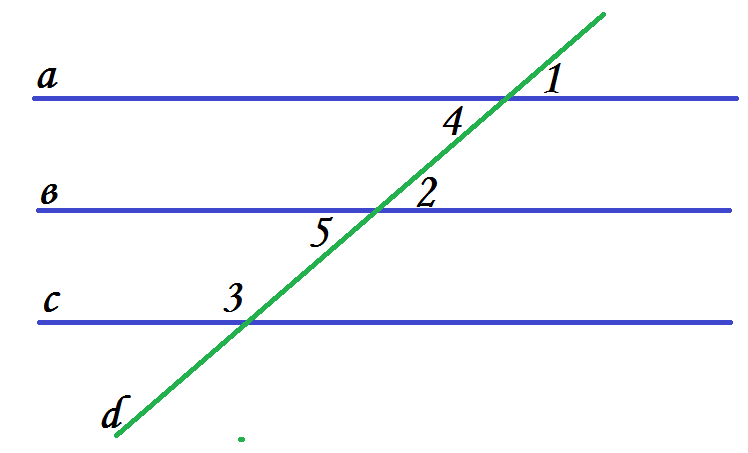

Дано:
1=2
2+3=1800
Доказать: aǁb
Доказать: а ǁ с
- Переносим рисунок в тетрадь и самостоятельно решаем. (2-3 мин.).
- Все ли у нас есть, чтобы ответить на вопрос? (нет)
- А что мы можем сначала доказать? (что aǁb).
- А для чего мы рассмотрели эту задачу? (такой кусочек есть в нашей задаче).
- Итак, мы доказали, что aǁb и что bǁс, какой вывод мы можем сделать? (aǁс). Почему? (по следствию из аксиомы параллельных прямых).
Итак, мы доказали, что aǁb и что bǁс, какой вывод мы можем сделать? (aǁс). Почему? (по следствию из аксиомы параллельных прямых).

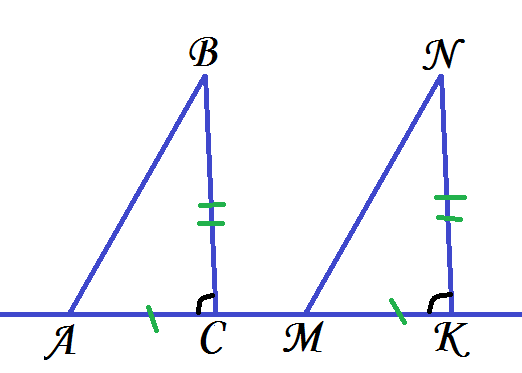
Доказать, что
1) ВСǁNK
2) АВǁМN
-
Задача 6.
(У доски один решает задачу вместе с классом. Пока дети переносят рисунок в тетради, ученик продумывает решение).
- Итак, что нам необходимо доказать? (NKǁВC).
- Что необходимо иметь, чтобы это доказать? (какие-либо данные для использования одного из признаков параллельности).
- Что нам известно? (что NKM равен BCА).
- А эти углы какие при прямых ВС и NK и секущей АК? (соответственные)
- Делаем вывод. (Прямые NKǁВC по равенству соответственных углов).
- Проверяем вторую часть задачи (сначала идет устная проверка, исправление ошибок, потом дети переносят решение себе в тетради).
- А если нам известно, что прямые параллельны, то, что мы можем сказать об углах, образованных этими прямыми и секущей? (что накрест лежащие углы равны, соответственные углы равны и сумма односторонних углов равна 180о). Как эти теоремы называются? (обратные).
- Сформулируйте обратную теорему. (При пересечении параллельных прямых секущей, накрест лежащие углы равны).
- Сформулируйте обратную теорему. (При пересечении параллельных прямых секущей, соответственные углы равны).
- Сформулируйте обратную теорему. (При пересечении параллельных прямых секущей, сумма односторонних углов равна 180о).
- Выберите верное утверждение.
- А что произойдет, если мы поменяем местами то, что дано и то, что доказать? (получим обратную задачу).
- Как ее будем решать? (т.к. прямые параллельны, то по теореме накрест лежащие углы будут равны, значит 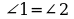 =32о).
=32о).
- Молодцы. Записываем следующую задачу 7
Д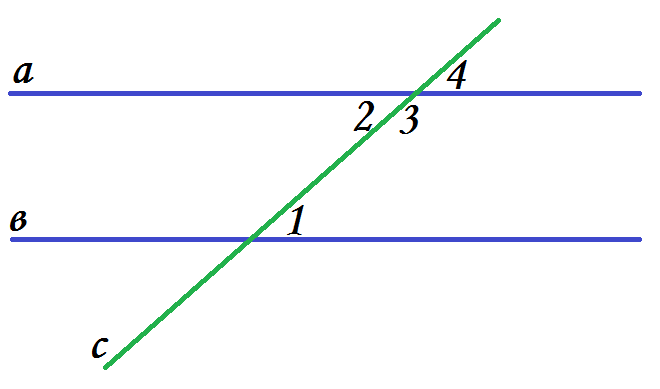 ано:
ано:
аǁв, 1=750
Найти: 2, 3, 4.
- Внимательно читаем условие. Какой вопрос перед нами?
- Чтобы решить эту задачу, что будем использовать? (обратную теорему).
- Почему и какую? (т.к. прямые параллельны, поочередно все три или можем воспользоваться свойствами вертикальных и смежных углов).
- Что нам известно о параллельных прямых, пересеченных секущей? (что накрест лежащие углы равны, соответственные углы равны, сумма односторонних углов равна 180о).
- Пожалуйста, что мы можем найти? �� 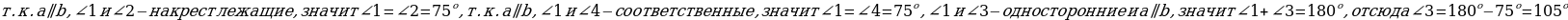
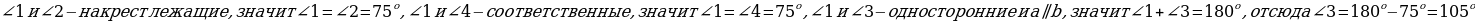 - Решили задачу? (да). Записываем ответ.
- Решили задачу? (да). Записываем ответ.
- Почему мы смогли найти требуемые углы? (т.к. мы знали, что прямые параллельны).
- А чем воспользовались для нахождения углов? (обратными теоремами).
- Возьмите листочки с заданием (прил. 2), подпишите фамилию и класс и быстренько ответьте на вопросы.
Если остается время решить задачи 8, 9, если нет, то перейти к подведению итогов.
4. Подведение итогов.
- Итак, с какими прямыми мы работали? (с параллельными).
- Как доказать, что прямые параллельны? (используя признаки параллельности прямых).
- Какие это признаки? (по равенству накрест лежащих, соответственных углов и по сумме односторонних углов).
- Что мы знаем об углах, образованных при пересечении параллельных прямых секущей? (что накрест лежащие, соответственные углы равны, а сумма односторонних углов равна 180о).
5. Домашнее задание.
- Молодцы, открываем дневники, записываем домашнее задание.
6. Рефлексия.
- Полезным ли для вас был данный урок? Что вы научились делать? Остались ли «темные» места в ваших знаниях по данной теме?
- Оценки за урок получают: …..
- Урок окончен, спасибо за работу, до свидания.







 Рис. 1
Рис. 1 Определение Углы 3 и 5; 4 и 6 называются накрест лежащие.
Определение Углы 3 и 5; 4 и 6 называются накрест лежащие. Выберите верные утверждения.
Выберите верные утверждения. Рис. 3
Рис. 3
 Рис. 5
Рис. 5




 адача 1. Дано:
адача 1. Дано: 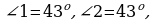 Доказать, что aǁb.
Доказать, что aǁb.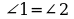 , а они накрест лежащие при прямых a и b и секущей с , значит прямые параллельны по равенству накрест лежащих углов. ч.т.д.)
, а они накрест лежащие при прямых a и b и секущей с , значит прямые параллельны по равенству накрест лежащих углов. ч.т.д.)
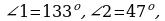 Доказать, что aǁb.
Доказать, что aǁb.
 адача 2. Задача 3.
адача 2. Задача 3. 
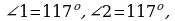 Доказать, что aǁb.
Доказать, что aǁb. адача 4.
адача 4. 
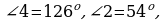 Доказать, что aǁb.
Доказать, что aǁb.
 - Ответьте на вопрос, параллельны ли прямые а и b, если:
- Ответьте на вопрос, параллельны ли прямые а и b, если: 

 Итак, мы доказали, что aǁb и что bǁс, какой вывод мы можем сделать? (aǁс). Почему? (по следствию из аксиомы параллельных прямых).
Итак, мы доказали, что aǁb и что bǁс, какой вывод мы можем сделать? (aǁс). Почему? (по следствию из аксиомы параллельных прямых).
 ано:
ано: 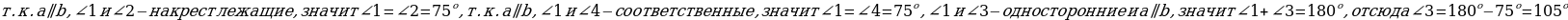
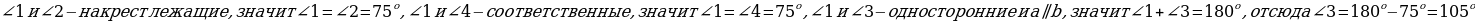 - Решили задачу? (да). Записываем ответ.
- Решили задачу? (да). Записываем ответ.









