ОГЭ по информатике. Задание № 3.

Задание № 3

Логические значения, операции, выражения.

Уровень сложности – базовый.

Максимальный балл за задание – 1.

Примерное время на выполнение задания (мин) - 3

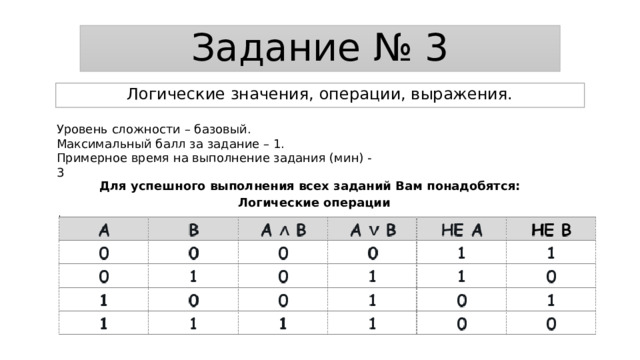
Для успешного выполнения всех заданий Вам понадобятся:

Логические операции

Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложенное выражение ложно.

Обозначение: F = A & B. Другие обозначения:   Λ , · , и, and .

Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выражения ложны.

Обозначение: F = A v B. Другие обозначения: +, I, или, or.

Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.

Обозначение: F = ¬A. Другие обозначения: нет, not, A .

Приоритет логических операций . Если в выражениях нет скобок, то очередность выполнения логических операций следующая:

1)  отрицание;  2)  конъюнкция;  3)  дизъюнкция. 

= 5 Х НЕ Х Х = 10 Формула де Моргана НЕ (A и В) НЕ A или НЕ В НЕ A и НЕ В НЕ (А или В) " width="640"

Логические значения, операции, выражения.

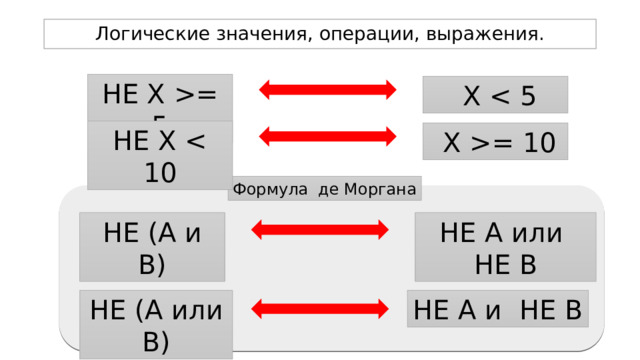
НЕ Х = 5

Х

НЕ Х

Х = 10

Формула де Моргана

НЕ (A и В)

НЕ A или НЕ В

НЕ A и НЕ В

НЕ (А или В)

14) и (Х 3. Значит, наибольшее число, для которого высказывание будет истинным — 18 В ответе (число) - 18 18 14 " width="640"

Логические значения, операции, выражения.

Пример 1.

1

=

1

1

Алгоритм решения

1. В составном высказывание используется отрицание. Откажемся от него.

2. Задача сводится к определению наибольшего целого Х , для которого верны оба утверждения.

(Х 14) и (Х

3. Значит, наибольшее число, для которого высказывание будет истинным — 18

В ответе (число) - 18

18

14

7) или (Х Оно будет ложным, когда 3. Значит, числом, для которого высказывание будет ложным — 7 (Х 6) В ответе (число) - 7 7 6 " width="640"

Логические значения, операции, выражения.

Пример 2.

0

=

0

0

Алгоритм решения

1. В составном высказывание используется отрицание. Откажемся от него.

2. Задача сводится к определению целого Х , для которого ложны оба утверждения.

(Х 7) или (Х

Оно будет ложным, когда

3. Значит, числом, для которого высказывание будет ложным — 7

(Х 6)

В ответе (число) - 7

7

6

Логические значения, операции, выражения.

Пример 3.

=

1

1

1

Алгоритм решения

1. В составном высказывание используется отрицание. Откажемся от него.

2. Задача сводится к определению наибольшего целого Х , для которого верны оба утверждения.

(Х четное) и (Х

3. Значит, наибольшим четным числом, будет число 8

В ответе (число) - 8

10

Логические значения, операции, выражения.

Пример 4.

1

=

1

1

Алгоритм решения

1. В составном высказывание используется отрицание. Откажемся от него.

2. Задача сводится к определению наименьшего двузначного числа у которого первая цифра четная и всё число делится на три.

(первая цифра четная) и (число делится на 3)

Вспомним эти числа, 21,24,27.

3. Значит, наименьшее число, для которого высказывание будет истинным — 21.

В ответе (число) - 21

= 15) И НЕ (X И (Х нечётное) Пример 5. 1 = 1 1 Алгоритм решения 1. В составном высказывание используется отрицание. Откажемся от него. 2. Числа, удовлетворяющие указанным границам: ((Х И (X = 8)) И (Х нечётное) 3. Выбираем все нечётные 8, 9, 10, 11, 12, 13, 14. 4. Читаем внимательно условие! Определить количество натуральных чисел. 9,11,13 В ответе (число) - 3 8 15 " width="640"

Логические значения, операции, выражения.

Определите количество натуральных чисел х, для которых логическое выражение истинно:

( НЕ (Х = 15) И НЕ (X И (Х нечётное)

Пример 5.

1

=

1

1

Алгоритм решения

1. В составном высказывание используется отрицание. Откажемся от него.

2. Числа, удовлетворяющие указанным границам:

((Х И (X = 8)) И (Х нечётное)

3. Выбираем все нечётные

8, 9, 10, 11, 12, 13, 14.

4. Читаем внимательно условие! Определить количество натуральных чисел.

9,11,13

В ответе (число) - 3

8

15

Логические значения, операции, выражения.

Напишите наименьшее двузначное число  x , для которого истинно высказывание:

(ТОЛЬКО ПЕРВАЯ ЦИФРА НЕЧЁТНАЯ) И НЕ (ЧИСЛО ДЕЛИТСЯ НА 4) И (ЧИСЛО ДЕЛИТСЯ НА 5)

Пример 6.

1

=

1

1

1

Алгоритм решения

1. В составном высказывание используется отрицание. Откажемся от него.

2. Числа, удовлетворяющие указанным условиям:

(ТОЛЬКО ПЕРВАЯ ЦИФРА НЕЧЁТНАЯ) И (ЧИСЛО не ДЕЛИТСЯ НА 4) И (ЧИСЛО ДЕЛИТСЯ НА 5)

3. Выбираем наименьшее двузначное

10,15,30,35,50,55,70,75,90,95

Первая цифра десятка – нечётная, само число не делится на 4, но делится на 5

4! Смотрим, что требуется в ответе: «наименьшее двузначное число»

10

В ответе (число) - 10

Логические значения, операции, выражения.

Пример 7.

Определите количество натуральных двузначных чисел х, для которых истинно логическое выражение: НЕ ( х чётное) И НЕ (х кратно 5)

1

=

1

1

Алгоритм решения

1. В составном высказывание используется отрицание. Откажемся от него.

2. Как определить искомое количество?

(х нечётное) И (x не кратно на 5)

Общее количество натуральных двузначных чисел равно 90.

3. Следовательно, количество нечётных натуральных двузначных чисел, не кратных 5 равно:

4! Смотрим, что требуется в ответе: «количество»

Из них нечётных 45

45 - 9 = 36

(99 – 10 + 1) = 90.

В числе этих 45 не учитываем числа кратные 5.

В ответе (число) - 36

Это числа(15,25,35,45,55,65,75,85,95). Их 9

= 8) И ( х нечётное ) 3. Перебираем числа из указанного промежутка [8; 14) и все нечётные 4! Смотрим, что требуется в ответе: «количество» 9,11,13 В ответе (число) - 3 " width="640"

Логические значения, операции, выражения.

Пример 8.

1

=

1

1

1

Алгоритм решения

1. В составном высказывание используется отрицание. Откажемся от него.

2. Определим искомый промежуток

(х И (x = 8) И ( х нечётное )

3. Перебираем числа из указанного промежутка

[8; 14) и все нечётные

4! Смотрим, что требуется в ответе: «количество»

9,11,13

В ответе (число) - 3