Открытый урок по геометрии ”Векторный способ решения задач в рамках подготовки к ЕГЭ”, 11 класс

Открытый урок

по теме "Векторный способ

решения задач в рамках подготовки к ЕГЭ."

(11 класс, геометрия)

учитель математики МБОУ "СОШ №42"

г.Курска

Шамбазова Г.С.

Тема урока:

Векторный способ решения задач в рамках подготовки к ЕГЭ.

План урока: урок-закрепление знаний.

Место урока в курсе геометрии:

Л.С. Атанасян "Геометрия 10-11 класс".

Цель урока:

Обучающая :

систематизация основных методов решения задач по теме урока.

Развивающие:

формирование и развитие общеучебных умений и навыков: обобщения, сравнение, анализа, синтеза, поиска способов решения. Развитие пространственных представлений средствами компьютерной анимации.

Воспитательные:

воспитание культуры групповой работы, воспитание внимания, взаимопомощи.

(Цель урока формулируют учащиеся)

Ход урока.

Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу-это значит пережить приключение.

В.Произволов

I)Актуализация знаний.

1)Проверка домашнего задания.

(решения домашних задач проецируются на экран)

Акцентрировать внимание на задаче №3.

Задача №1

Решение задачи №1

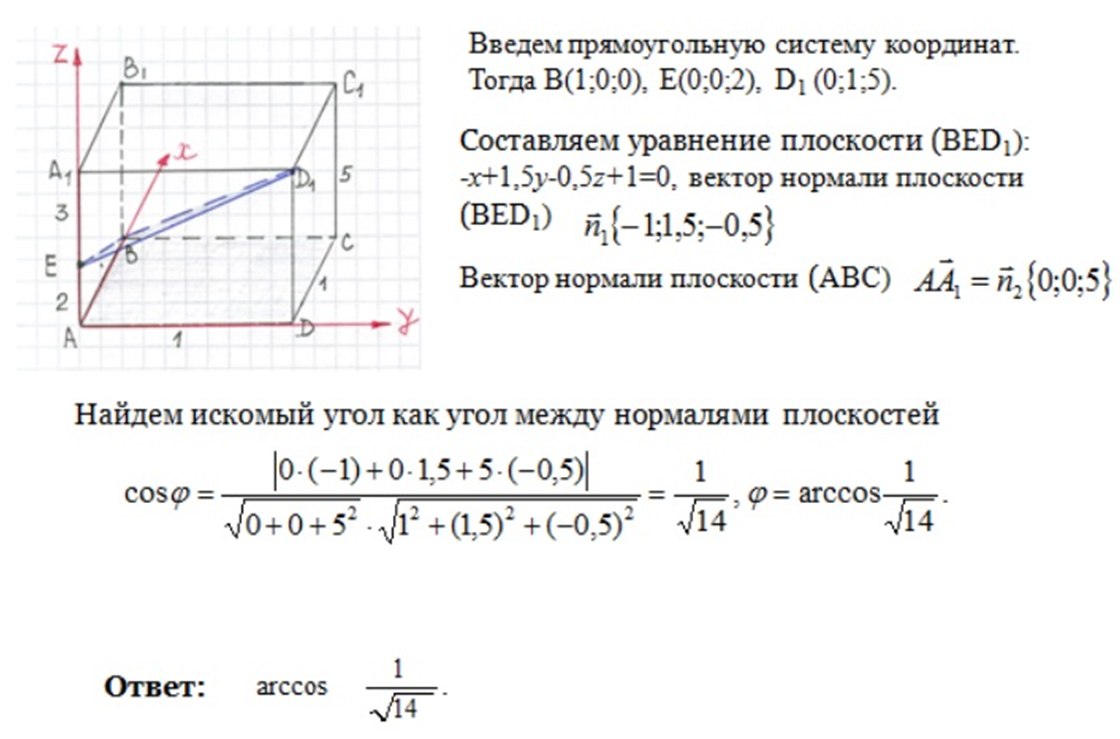
Задача №2

Решение задачи №2

Задача №3

Решение задачи №3

В ходе проверки домашней работы повторить нахождение углов (между прямыми, между прямой и плоскостью, плоскостями).

II) Применение теоретического материала к решению задач.

Как и большинство задач, задачи C2(№14) из ЕГЭ можно решить различными способами.

Один из них координатно-векторный.

За неделю до этого урока учащиеся получили модули из 7 задач, часть которых будут рассмотрены на уроке. А еще рассмотреть доказательство теоремы о трех перпендикулярах векторным и одним из аналитических способов.

К доске одновременно вызываются 3 ученика:

- один доказывает теорему о трех перпендикулярах двумя способами

- второй решает задачу № 1

- третий решает задачу № 2

Условия задач:

№1

Вершины тетраэдра ABCD имеют координаты A(3;-1;0), B(0;-7;3), C(-2;1;-1) , D(3;2;6). Докажите, что прямая AD перпендикулярна к плоскости ABC.

№2

В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1.

(Ответ: .)

Пока учащиеся у доски решают, класс получает самостоятельную работу в два варианта с последующей проверкой на уроке(работают парами,один вариант на двоих),еще один третий вариант(более сложный) дополнительно для тех,кто справился раньше. (условия на листочках)

Условия задач:

№1 Составьте уравнения плоскости, проходящей через три точки с заданными координатами.

I)Вариант

A(1;0;2), B(0;1;-1), C(0;-2;0)

II)Вариант

A(1;1;1), B(-1;2;1), C(1;-2;-2)

III)Вариант (дополнительный)

Найдите расстояние от точки M(4;-1;2) до плоскости, проходящей через три точки с заданными координатами A(1;0;1), B(0;2;8), C(3;-2;9)

Ответы:

I) 8x-y-3z-2=0

II) x+2y-2z-1=0

III) 15x+11y-z-14=0

(уравнение плоскости)

ρ(M,ABC)=

После проверки задач №1,№2 и обсуждения теоремы о трех перпендикулярах, проверки самостоятельной работы, рассмотреть еще один способ решения задачи №1.

III. Итоги урока (рефлексия)

Выставление отметок за урок.

IV.Домашнее задание (на карточках две задачи №14 из ЕГЭ, №1 рещить двумя способами(координатно-векторный и аналитический), №2 координатно-векторным способом).

Условия задач:

№1 Решите задачу двумя способами:

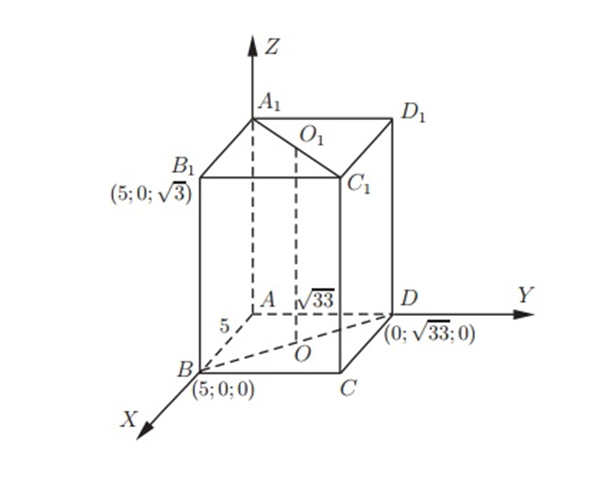
Сторона основания правильной треугольной призмы АВСА1В1С1 равна 2, а диагональ боковой грани равна . Найдите угол между плоскостью А1ВС и

плоскостью основания призмы.

№2Решите задачу координатно-векторным способом:

Основанием прямой треугольной призмы ABCA1B1C1 является равнобедренный треугольник ABC, в котором AB=BC=20, AC=32. Боковое ребро призмы равно 24. Точка P принадлежит ребру BB1, причем

BP : PB1 = 1 : 3

a) Пусть М-середина A1C1.

Докажите,что прямые MP и AC перпендикулярны.

б) Найдите тангенс угла между плоскостями A1B1C1 и ACP.

(Ответы №1 30

№2 б) 0,5.)