Перпендикулярность плоскостей

Практическое занятие Приложение 7

Решение задач по теме «Перпендикулярность плоскостей». Теорема о трех перпендикулярах. Признаки и свойства параллельных и перпендикулярных плоскостей. Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми, между произвольными фигурами в пространстве.

1) Подготовительный этап

П ерепишите и заполните пропуски:

Пример 1. Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найдите длину отрезка АВ если: АС = 6 м, ВD = 7 м, СD = 6 м. (рис.)

Решение:

Дано: α ⊥ β, A , B , АС ⊥СD, ВD ⊥ CD, АС = 6 м, ВD = 7 м, СD = 6 м.

Найти: АВ

Решение: т.к. α ⊥ β, АС ⊥СD, ВD ⊥ CD, то из прямоугольного Δ АСВ по теореме Пифагора: АВ² = АС² + ВС², но из прямоугольного Δ СDВ по теореме Пифагора следует, что: ВС² = СD² + ВD² , так что АВ² = АС² + СD² + ВD².

АВ² = 6² + 7² + 6² = 36 + 49 + 36 = …, АВ = …

Ответ: 11 м

Пример 2. Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найдите длину отрезка АВ если: АD = ВС = 5 м, СD = 1 м. (рис. из примера 1)

Решение:

Дано: α ⊥ β, A , B , АС ⊥СD, ВD ⊥ АD, АD = ВС = 5 м, СD = 1 м

Найти: АВ

Решение: т.к. α ⊥ β, АС ⊥СВ и ВD ⊥ CD, то из прямоугольного Δ АСВ по теореме Пифагора: АВ² = АС² + ВС², но из прямоугольного Δ СDА по теореме Пифагора следует, что: АС² = АD² – СD² , так что АВ² = АD² – СD² + ВС².

АВ² = 5² – 1² + 5² = 25 – 1 + 25 = …, АВ = …

Ответ: 7 м.

П ример 3. Точка А находится на расстоянии а = 24 см и b = 10 см от двух перпендикулярных плоскостей α и β. Найдите расстояние от этой точки до прямой пересечения плоскостей.

Решение:

Дано: α ⊥ β , α ∩ β = с, ( А, = a, ( А, = b, а = 24 см, b = 10 см

Найти : (А, с)

Решение: Проведем перпендикуляры АВ, АD, АС. Тогда четырехугольник АВСD – прямоугольник. АС² = а² + b² , (А, с) = АС. ВС - проекция АС на плоскость α, поэтому по ТТП: ВС ⊥ с, ВС ⊥ β. Так как АD ⊥ β, то по теореме АD ||ВС, значит, АD и ВС лежат в одной плоскости.

Итак, АС² = 24² + 10² = 576 + 100 = … , АС = …

Ответ: АС = 26 см.

П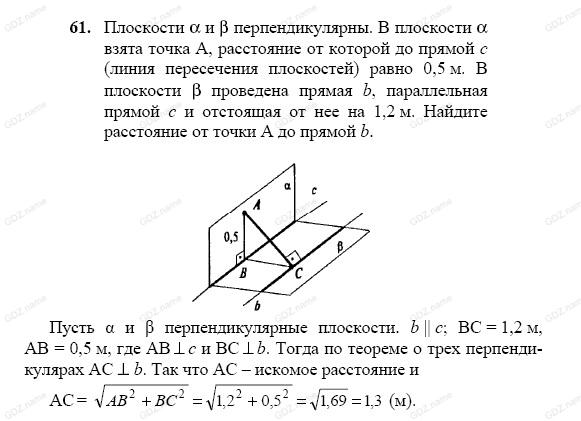 ример 4. Плоскости α и β перпендикулярны. В плоскости α взята точка А, расстояние от которой до прямой с (линия пересечения плоскостей ) равно 0,5 м. В плоскости β проведена прямая b, параллельная прямой с и отстоящая от нее на 1,2 м. Найдите расстояние от точки А до прямой b.

Решение:

Дано: α ⊥ β , b || с, АВ ⊥с, ВС ⊥ b, ВС = 1, АВ = 0,5м.

Найти: (А,b)

Решение: т.к. α ⊥ β , b || с, АВ ⊥с, ВС ⊥ b, то по ТТП АС ⊥ b. Так что (А,b) = АС и из прямоугольного Δ АСВ по теореме Пифагора АС² = АВ² + ВС² = 1,2² + 0,5² = 1,44 + 0 ,25 = …, АС = …

Ответ: АС = 1,3 м.

Пример 5. Перпендикулярные плоскости α и β пересекаются по прямой с. Плоскости α проведена прямая а || с, в плоскости β – прямая b || с. Найдите расстояние между прямыми а и b , если расстояние между прямыми а и с равно 1,5 м, а между прямыми b и с – 0,8 м.

Решение:

Д ано: α ⊥ β , α ∩ β = с, а , b , а || с, b || с

Найти: (а,b)

Решение: Возьмем в плоскости α точку А на прямой а. По теореме о трех параллельных прямых получаем, что а || b (так как а || с, b ||с). Проведем АС ⊥с и СВ ⊥ b. Тогда по ТТП АВ ⊥ b.

Так что (а,b) = АВ и АВ ⊥ СВ, так как α ⊥ β ( по условию), из прямоугольного Δ АВС по теореме Пифагора: АВ² = СВ² + АС² = 1,5² + 0,8² = 2,25 + 0,64 = … , АВ = …

Ответ: АВ = 1,7 м.

2) Практический этап

1. Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найдите длину отрезка АВ если: АС = 3 м, ВD = 4 м, СD = 12 м.

2. Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найдите длину отрезка АВ если: АD = 4 м, ВС = 7 м, СD = 1 м.

3. Точка А находится на расстоянии а = 17 см и b = 8 см от двух перпендикулярных плоскостей α и β. Найдите расстояние от этой точки до прямой пересечения плоскостей.

4. Плоскости α и β перпендикулярны. В плоскости α взята точка А, расстояние от которой до прямой с ( линия пересечения плоскостей ) равно 0,9 м. В плоскости β проведена прямая b, параллельная прямой с и отстоящая от нее на 1,2 м. Найдите расстояние от точки А до прямой b.

5. Перпендикулярные плоскости α и β пересекаются по прямой с. Плоскости α проведена прямая а|| с, в плоскости β – прямая b || с. Найдите расстояние между прямыми а и b , если расстояние между прямыми а и с равно 4,5 м, а между прямыми b и с – 2,4 м.

3) Дополнительные задания^*.

1. Дано: АС - перпендикуляр, АВ - наклонная,
   а) АВ = 10 см, ВС = 6 см, АС = ?

2. Телефонная проволока длиной 15 м протянута от телефонного столба, где она прикреплена на высоте 8 м от поверхности земли, к дому, где ее прикрепили на высоте 20 м. Найдите расстояние между домом и столбом, предполагая, что проволока не провисает.

Дано: AB = 15 м, АС = 8 м, BD = 20 м, Найти: CD.

(Указание: Δ BKА – прямоугольный, АK² = AB² - BK ²)

1. Из вершины равностороннего треугольника АВС проведен перпендикуляр АК к плоскости треугольника. Найдите длину АК, если ВС = 3 см, КС = 3 см.

2. Дано: ABCD квадрат; AM - прямая; АМ ⊥ (ABCD); АС ∩ BD = О. Доказать: a) BD ⊥ (АМО); б) МО ⊥ BD.

3. Прямые АВ и CD перпендикулярны некоторой плоскости и пересекают ее в точках В и D соответственно. Найдите AС, если АВ = 9, CD = 15, BD = 8.

4. Отрезок МН пересекает некоторую плоскость в точке К. Через концы отрезка проведены прямые HP и ME, перпендикулярные плоскости и пересекающие ее в точках Р и Е. Найдите РЕ, если HP = 4 см, НК = 5 см, ME = 12 см.