Правила по математике 2 класс

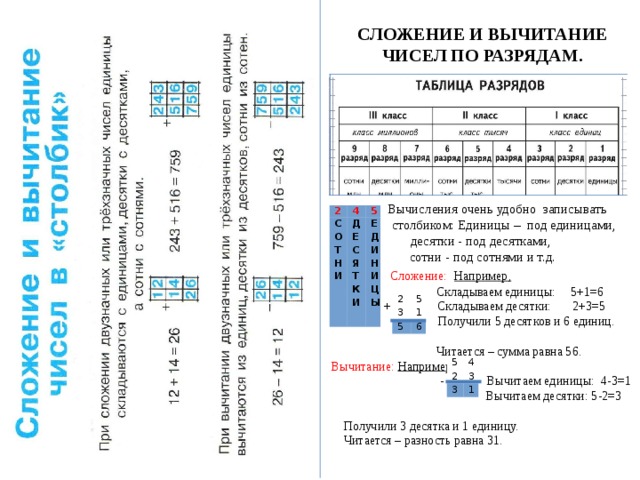
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ЧИСЕЛ ПО РАЗРЯДАМ.

Вычисления очень удобно записывать

столбиком: Единицы – под единицами,

десятки - под десятками,

сотни - под сотнями и т.д.

Сложение: Например,

Складываем единицы: 5+1=6

+ Складываем десятки: 2+3=5

Получили 5 десятков и 6 единиц.

Читается – сумма равна 56.

Вычитание: Например,

- Вычитаем единицы: 4-3=1

Вычитаем десятки: 5-2=3

Получили 3 десятка и 1 единицу.

Читается – разность равна 31.

2

С

4

Д

О

5

Е

Т

Е

Н

С

Д

И

И

Я

Н

Т

И

К

И

Ц

Ы

2

3

5

5

1

6

5

2

4

3

3

1

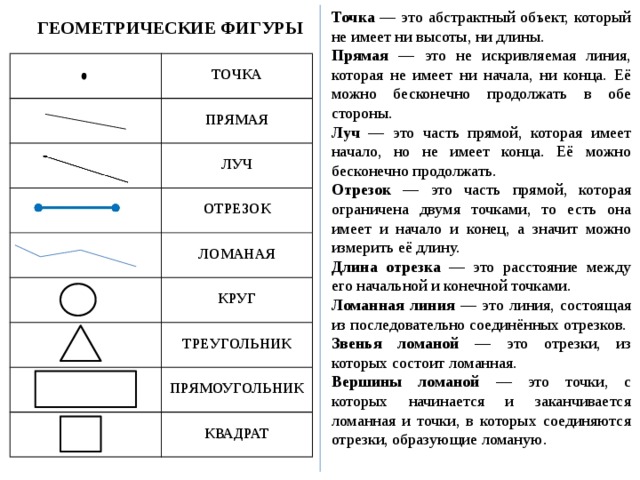
Точка — это абстрактный объект, который не имеет ни высоты, ни длины.

Прямая — это не искривляемая линия, которая не имеет ни начала, ни конца. Её можно бесконечно продолжать в обе стороны.

Луч — это часть прямой, которая имеет начало, но не имеет конца. Её можно бесконечно продолжать.

Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.

Длина отрезка — это расстояние между его начальной и конечной точками.

Ломанная линия — это линия, состоящая из последовательно соединённых отрезков.

Звенья ломаной — это отрезки, из которых состоит ломанная.

Вершины ломаной — это точки, с которых начинается и заканчивается ломанная и точки, в которых соединяются отрезки, образующие ломаную.

ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ

ТОЧКА

ПРЯМАЯ

ЛУЧ

ОТРЕЗОК

ЛОМАНАЯ

КРУГ

ТРЕУГОЛЬНИК

ПРЯМОУГОЛЬНИК

КВАДРАТ

Чтобы определить прямой угол или нет, нужно взять особый инструмент – угольник.

Если, приложив угольник к углу, вершиной к вершине, стороны совпадут, то угол - прямой . Не совпадут – непрямой.

Непрямые углы делятся на тупые и острые .

Угол, величина которого меньше величины прямого – острый,

Угол, величина которого больше величины прямого – тупой.

Прямоугольник – это четырёхугольник, у которого все углы прямые. Противополож-ные стороны прямоугольника равны.

Одним цветом показаны

противоположные стороны

прямоугольника.

Квадрат – это прямоугольник, у которого все стороны равны.

УГОЛ. ВИДЫ УГЛОВ.

Угол – это геометрическая фигура, состоящая из двух лучей, исходящих из одной точки.

Лучи, образующие угол, называются сторонами угла, общее начало называется вершиной.

Углы могут быть прямыми и непрямыми.

Как решить задачу?

1. Внимательно и выразительно прочитать задачу.

2. Представить себе то, о чём в ней говорится.

3. Выделить устно, что известно и что неизвестно.

4. Определить главный вопрос задачи.

5. Записать кратко условие задачи (краткую запись).

6. Составить и записать решение задачи.

7. Записать ответ.

Как оформит краткую запись?

Примеры:

• У Вани 3 яблока, а у Кати – 5 груш. Сколько всего фруктов у ребят?

Ваня – 3 яб.

Катя – 5 гр.

• Коля нашел 4 гриба, а Витя – 7 грибов. Кто нашел грибов больше и на сколько?

Коля – 4 г.

Катя – 5 г.

3. Дима купил 10 тетрадей, а Света на 6 меньше. Сколько тетрадей купила Света?

Дима – 10 т.

Света - ? т., на 6 т. меньше

4. Вера купила 9 карандашей, а Маша на 4 больше. Сколько карандашей купила Маша?

Вера – 9 к.

Маша - ? к., на 4 к. больше

УРАВНЕНИЕ.

ЭТО РАВЕНСТВО, СОДЕРЖАЩЕЕ НЕИЗВЕСТНОЕ ЧИСЛО, КОТОРОЕ НАДО НАЙТИ.

Неизвестное число обозначают маленькими латинскими буквами, например х (икс) или y (игрик).

Х+4=16 – это уравнение.

Х= 16-4 - это решение уравнения.

Х=12. - это решение уравнения.

12+4=16 - это проверка правильнос-

16=16 ти решения уравнения.

В первоначальное уравнение вместо неизвестного, т.е. Х ставим полученное значение. В данном примере – это число 12. Все остальное переписываем из первоначального уравнения. Решаем и проверяем равенство полученных значений с правой и левой стороны.

? Ф.

? г.

- скобка. Ставится в краткой записи задачи тогда, когда в вопросе звучит, что надо найти … всего…

УМНОЖЕНИЕ.

ДЕЛЕНИЕ.

Знак деления - :

Знаки умножения : или х

6 : 2 = 3

2 3 = 6

ДЕЛИМОЕ ЧАСТНОЕ

ДЕЛИТЕЛЬ

ПРАВИЛА ДЕЛЕНИЯ.

• Самое большое число в частном - делимое.
• На нуль делить нельзя!
• Если делимое равно делителю, то частное равно 1.

2 : 2 = 1

• Частное равно делимому, если делитель равен 1.

2 : 1 = 2

• Частное равно 0, если делимое равно 0.

0 : 2 = 0

1 МНОЖИТЕЛЬ ПРОИЗВЕДЕНИЕ

2 МНОЖИТЕЛЬ

ПРАВИЛА УМНОЖЕНИЯ.

• Если один из множителей равен 0 , то и произведение равно 0 .

2 х 0 = 0 или 0 3 = 0

• Если один из множителей равен 1, то произведение равно другому множителю.

3 х 1 = 3 или 1 3 = 3

• От перестановки множителей значение произведения не меняется.

3 х 5 = 5 х 3 или 3 5 = 5 3

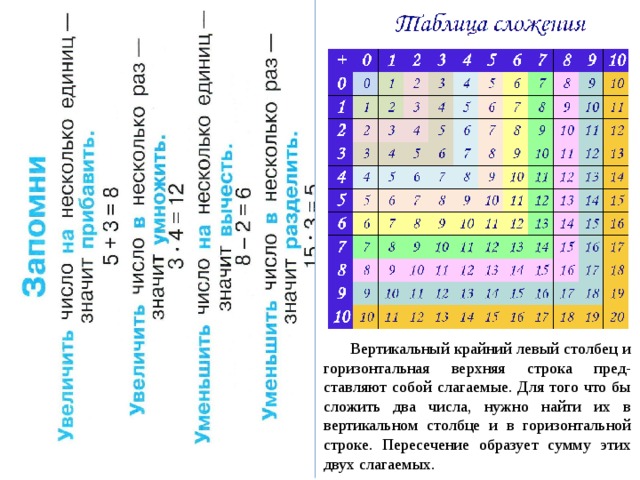
Вертикальный крайний левый столбец и горизонтальная верхняя строка пред- ставляют собой слагаемые. Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых.