Презентация к уроку геометрии по теме "Площади"

Если хотите научиться плавать – нужно войти в воду, а если желаете научиться решать задачи – решайте их.

Пойа Д.

Площадь многоугольника

.

Назовите формулу для нахождения площади данной фигуры

.

Назовите формулу для нахождения площади данной фигуры

.

Назовите формулу для нахождения площади данной фигуры

.

Назовите формулу для нахождения площади данной фигуры

.

Назовите формулу для нахождения площади данной фигуры

.

Назовите формулу для нахождения площади данной фигуры

Исправить формулу

.

Назовите формулу для нахождения площади данной фигуры

.

Решите задачи по готовому чертежу

9

.

Найдите площадь треугольника ABC

.

Найдите сторону АС прямоугольного треугольника АВС

.

Найдите высоту АН

.

Найдите площадь параллелограмма

.

Найдите площадь параллелограмма

.

Найдите площадь треугольника ADB

Дано:

S трапеции = 6 см ²

S ∆ ABC = 2c м ²

• S трапеции = 6 см ² S ∆ ABC = 2c м ²

Решение:

S ∆ ADB =1/2 · AB · AD = S ∆ ADC = 6 – 2 = 4 c м ²

.

Найдите площадь фигуры, изображенной на клетчатой бумаге

16

.

Площадь маленького квадрата равна 1, найти площадь многоугольника

.

Площадь маленького квадрата равна 1, найти площадь многоугольника

.

Площадь маленького квадрата равна 1, найти площадь многоугольника

.

Площадь маленького квадрата равна 1, найти площадь многоугольника

.

Площадь маленького квадрата равна 1, найти площадь многоугольника

.

Площадь маленького квадрата равна 1, найти площадь многоугольника

.

Площадь маленького квадрата равна 1, найти площадь многоугольника

.

Площадь маленького квадрата равна 1, найти площадь многоугольника

.

Практическая работа

25

.

Докажите, что медиана треугольника делит его на два треугольника равной площади

Дано:

∆ ABC,

BM- медиана.

Доказать:

S ∆ ABM=S ∆ MBC

.

Доказательство:

Треугольники AMB и ____ имеют общую

высоту, проведенную из вершины ___ .

По следствию 2: _________ площадей этих

треугольников равно отношению их

оснований, то есть

S ∆ ABM : _______ = AM : _____ .

Так как AM_M С по ________

медианы, то S ∆ ABM :S ∆ BMC = __ ,

следовательно, S ∆ ABM __ S ∆ BMC

MBC

B

отношение

S ∆ MBC

MC

свойству

=

1

=

.

Если высоты двух треугольников равны, то их площади относятся как основания.

Следствие из теоремы о площадях треугольника

28

.

Диагонали трапеции KHMP пересекаются в точке С

Докажите, что:

а) S ∆ KHM = S ∆ PHM ;

б) S ∆ KHC = S ∆ PMC .

28

.

а) S ∆ KHM = S ∆ PHM

Решение:

Пусть KB и PA перпендикуляры, проведенные из вершин K и P к прямой HM.

Отрезки KB и PA являются _________ трапеции KHMP , следовательно, KB__PA.

Так как равные отрезки KB и PA являются ________ треугольников KHM и PHM, имеющих общее

основание ___ , то

S ∆ KHM __S ∆ PHM .

высотами

=

высотами

HM

=

28

.

б) S ∆ KHC = S ∆ PMC

Решение:

Треугольники ∆ KHM и ∆ PHM составлены из треугольников ∆ KHC, ∆ HMC и ∆ PMC, значит, по свойству __ измерения площадей

S ∆ KHM = S ∆ KHC __ S ∆ CHM и S ∆ PHM = S ∆ PMC + S ∆ ____ .

В пункте а) доказано, что S ∆ KHM = S ∆ ____ , поэтому S ∆ KH С __ S ∆ PMC .

2

+

CHM

PHM

=

28

.

Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

Свойство измерения площадей

32

.

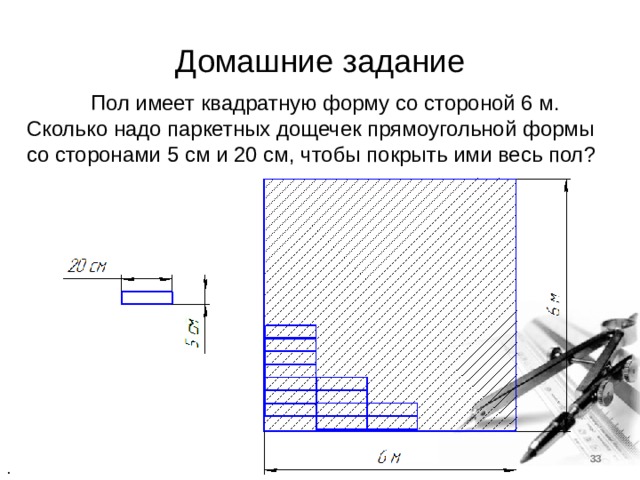
Домашние задание

Пол имеет квадратную форму со стороной 6 м. Сколько надо паркетных дощечек прямоугольной формы со сторонами 5 см и 20 см, чтобы покрыть ими весь пол?

32

.

Домашние задание

Сколько требуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими часть стены, имеющей форму прямоугольника со сторонами 4 м и 2,5 м ?

.

Площадь многоугольника

35

.