Презентация на тему: Изгиб прямого бруса

Тема: Изгиб прямого бруса

Преподаватель ГБУ КО ПОО «КИТиС» А.Н.Панина

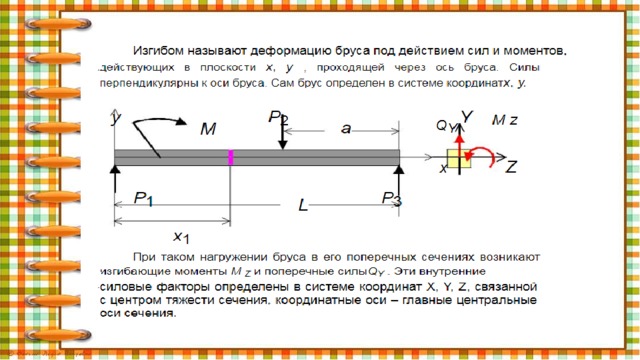
Внутренние силовые факторы при изгибе

• Поперечная сила , возникающая в сечении балки –это внутреннее усилие, равное алгебраической сумме проекций внешних сил, действующих по одну сторону от этого сечения на плоскость поперечного сечения.
• Изгибающий момент в сечении балки –это внутреннее усилие, равное алгебраической сумме моментов внешних сил, действующих по одну сторону от этого сечения, относительно центра тяжести сечения.

Правило знаков

• Положительная поперечная сила поворачивает рассматриваемую часть балки по часовой стрелке
• (кратко –по часовой плюс, против –минус, рис.1,а).
• Положительный изгибающий момент соответствует
• (т.е. вызывает) растяжению нижних волокон.

• Для отыскания опасного сечения строят эпюры Qy и Мх, используя метод сечения , либо метод характерных точек.
• Эпюра –это график, показывающий изменение того или иного фактора по оси балки.
• Сечения расставляются на характерных участках, характерный участок балки –это участок между какими либо изменениями. Изменения –это сосредоточенные силы или моменты, начало и конец распределенной нагрузки. Характерные точки –это точки, сколь-либо заметные на балке, т.е. точки приложения сосредоточенных сил, моментов и т.д

Основные закономерности при построении эпюр Qy и Mx

1.На участке балки, где отсутствует распределенная нагрузка, эпюра Qy-прямая, параллельная базовой линии, а эпюра Мх-наклонная прямая.

2.Под сосредоточенной силой на эпюре Qy наблюдается скачок, численно равный приложенной внешней силе, а на эпюре Мх–излом.

3.В точке приложения сосредоточенной пары сил(момента)на эпюре момента происходит скачок на размер момента этой пары, а эпюра Qy не претерпевает изменений.

4.На участке действия равномерно распределенной нагрузки эпюра Qy выражается наклонной прямой, а эпюра Мх –параболой, обращенной выпуклостью навстречу действию распределенной нагрузки.

5.Если на участке действия распределенной нагрузки эпюра пересекает базовую линию, то в этом сечении изгибающий момент принимает экстремаль-ное значение.

6.Если на границе действия распределенной нагрузки не приложено сосредоточенных сил, то на эпюре Qy участок, параллельный оси абсцисс, переходит в наклонный без скачка, а параболическая и наклонная части эпюры Мх сопрягаются плавно без изгиба.

7.Изгибающий момент в концевых сечениях балки всегда равен нулю, за исключением случая, когда в концевом сечении действует сосредоточенная пара сил. В этом случае изгибающий момент в концевом сечении балки равен моменту действующей пары сил

8.В сечении, соответствующем заделке, Qy и Мх численно равны опорной реакции и реактивному моменту заделки.

Последовательность решения задачи:

• 1) Найти опорные реакции балки (для консоли их можно не находить);
• 2) Балку разделить на участки, границами которых являются сечения, в которых приложены: сосредоточенные силы, сосредоточенные моменты, начинается или заканчивается равномерно распределенная нагрузка;
• 3) Выбрать расположение координатных осей, совместив ось z с осью балки, а оси у и х расположить в плоскости сечения (обычно ось у расположена вертикально);
• 4) Применяя метод сечений, вычислить значения поперечных сил в характерных сечениях и построить эпюру поперечных сил. Если поперечная сила, изменяясь непрерывно, проходит через нулевое значение, то необходимо определить аппликату ( z ) сечения, где Q обращается в нуль;
• 5) Применяя метод сечений, вычислить значения изгибающих моментов в характерных сечениях и построить эпюру изгибающих моментов.
• Для определения экстремальных значений изгибающих моментов дополнительно определить моменты в сечениях, где эпюра поперечных сил проходит через нулевое значение;
• 6) Используя дифференциальные зависимости, проверить правильность построения эпюр поперечных сил и изгибающих моментов;
• 7) Из условия прочности определить осевой момент сопротивления сечения балки в сечении, где изгибающий момент имеет наибольшее по модулю значение;
• 8) Используя таблицы ГОСТ или формулы для определения осевых моментов сопротивления простых плоских сечений (прямоугольник, круг), определить размеры поперечного сечения балки.

Пример 1

Пример 2

• Жестко заделанная консольная балка АВ нагружена, как показано на рис. (1.а) . Построить эпюры Q y и M x , подобрать сечение в форме двутавра.
• Дано : F =20 кН; q =21 кН/м; М =28 кН∙м; [ σ ]=160 МПа.
• НАЙТИ: Q y ; М х ; W х .

Решение:

• 1. Изобразим балку ( рис1. а ).
• 2. Делим балку на участки по характерным точкам: ВС , СD, DA .
• 3. Определяем Q y на каждом участке и строим эпюру ( рис.1, б ):
• ВС , сечение I-I, слева, 0≤ z 1 ≤3 м Q y1 =0.
• СD , сечение II-II, слева, 0≤ z 2 ≤2 м; Q y2 = F =20 кН.
• DA, сечение III-III, слева, 0≤ z 3 ≤2 м, Q y3 = F-q · z 3 ,
• при z 3 = 0 Q y3 = F =20 кН; при z 3 = 2 м Q y3 = F-q ·2=20-21·2=20-42=-22 кН.
• Q y3 =0 при z 3 ' =0,95 м.
• 4. Определяем М х на каждом участке и строим эпюру (см. рис 1. в ):
• ВС , сечение I-I, слева, 0≤ z 1 ≤3 м; М х1 = М =28 кН∙м.
• СD , сечение II-II, слева, 0  z 2  2 м, М х2 = М - Fz 1 ,
• при z 2 =0 М х2 = М =28 кН∙м; при z 2 =2 м М х2 = М - F· 2=28-20·2=-12 кН·м.
• DA, сечение III-III, слева, 0  z 3  2 м, М х3 = М-F ( z 2 +2)+ qz 2 /2,
• при z 2 =0, М х3 =28-20·2=-12 кН·м;
• при z 2 =2м, М х3 =28-20·4+21·2 2 /2=-10 кН·м;
• при z 2 =0,95м, М х3 =28-20·2,95+21·0,95 2 /2=-21,5 кН·м.
• Исходя из эпюры М х .:  М х max  =28 кН·м=28·10 6 Н·мм.
• 5. Определяем осевой момент сопротивления сечения :
• W x ≥  М х max  /[ σ ]; W x ≥28000000/160≥175000 мм 3 ≥175 см 3 .
• По ГОСТ 8239-89 выбираем двутавр № 20 с W х =184 см 3 .
• ОТВЕТ: W х =184 см 3 ― двутавр № 20 по ГОСТ 8239-89

Задания для самостоятельного решения

Контрольные вопросы

1.При изгибе в поперечном сечении бруса возникают ________ и _________ напряжения.

2.При построении эпюр следует помнить :

• ☺ на участке с распределенной нагрузкой эпюра «Q» - _________ прямая;
• ☺ в сечении с сосредоточенной силой на эпюре «Q» - _________________;
• ☺ на участке с распределенной нагрузкой эпюра «М» - ________________;
• ☺ в сечении с моментом на эпюре «М» - _____________;
• ☺ если на участке с распределенной нагрузкой эпюра «Q» пересекает ось, то на эпюре «М» - вершина ______________ .

3. Для выявления опасного сечения в изгибаемом элементе следует строить эпюры внутренних силовых факторов

• «Q» - ______________________;
• «М» -______________________ .
•  

Контрольные вопросы:

• 4. Какие разновидности связей используют при проектировании балок?
• 5. Какой изгиб называется чистым?
• 6. Какой изгиб называется поперечным?
• 7. Как определить знаки поперечной силы и изгибающего момента?
• 8. Как изменяется поперечная сила в сечении балки, к которому приложена сосредоточенная сила?
• 9. Как распределены нормальные напряжения по поперечному сечению балки?
• 10. Как определить нормальное напряжение в любой точке данного поперечного сечения при прямом изгибе?
• 11. Какие формы поперечных сечений являются рациональными для балок из пластических материалов?