

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Была в сети 05.02.2022 21:04

Шустова Наталия Владимировна
учитель математики
Местоположение
Россия, с. Никольское
Специализация
Презентация Применение производной
Категория:
Алгебра
05.02.2022 20:54



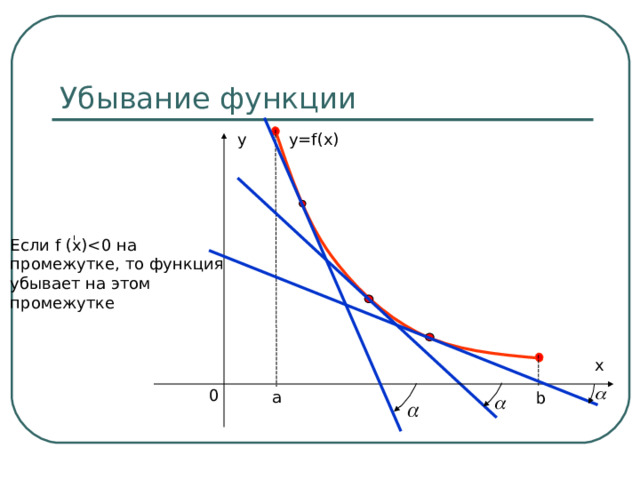
 0 на промежутке, то функция возрастает на этом промежутке x а 0 b " width="640"
0 на промежутке, то функция возрастает на этом промежутке x а 0 b " width="640"

 о х о х о f( х ) f( х ) f( х ) f( х ) о о x х 0 о " width="640"
о х о х о f( х ) f( х ) f( х ) f( х ) о о x х 0 о " width="640"

 0 1 х х х х f’(x)=0 2 4 1 3. х = -4, -2, 0, 3 – точки экстремумов функции у= f(x) . 3 _ _ - 0 1 х f’(x) 4. х = - 2 , х = 3 – точки максимумов функции. 2 4 5. х = - 4 , х = 0 – точки минимумов функции. 3 1 " width="640"
0 1 х х х х f’(x)=0 2 4 1 3. х = -4, -2, 0, 3 – точки экстремумов функции у= f(x) . 3 _ _ - 0 1 х f’(x) 4. х = - 2 , х = 3 – точки максимумов функции. 2 4 5. х = - 4 , х = 0 – точки минимумов функции. 3 1 " width="640"










