Презентация "Решение задач ЕГЭ при помощи теоремы Менелая и координатного метода"

Решение задач ЕГЭ при помощи теоремы Менелая и координатного метода

Учитель математики ГБОУ СОШ№15

Г. Севастополя

Василенко И.В.

Теорема Менелая

• Если на сторонах  AB  и  BC  треугольника  ABC  взяты соответственно точки  C 1  и  A 1 , а точка  B 1  взята на продолжении стороны  AC  за точку  C  (рис.1), то точки  C 1 ,  A 1  и  B 1  лежат на одной прямой  тогда и только тогда , когда выполнено равенство

Задача №1

Вставка рисунка

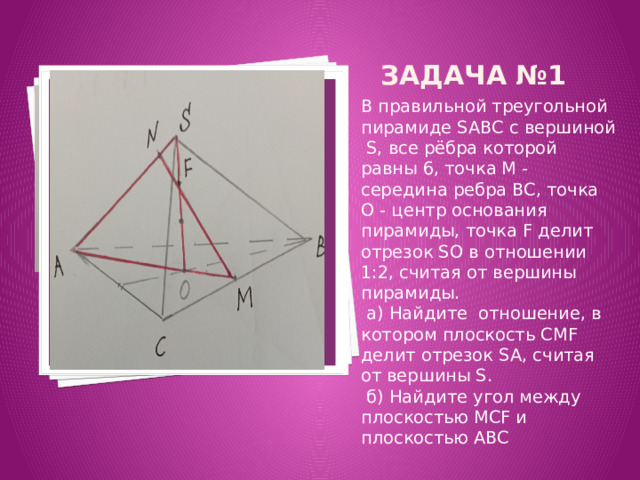
В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 6, точка M - середина ребра BC, точка O - центр основания пирамиды, точка F делит отрезок SO в отношении 1:2, считая от вершины пирамиды.

a) Найдите отношение, в котором плоскость CMF делит отрезок SA, считая от вершины S.

б) Найдите угол между плоскостью MCF и плоскостью ABC

Задача№2

Вставка рисунка

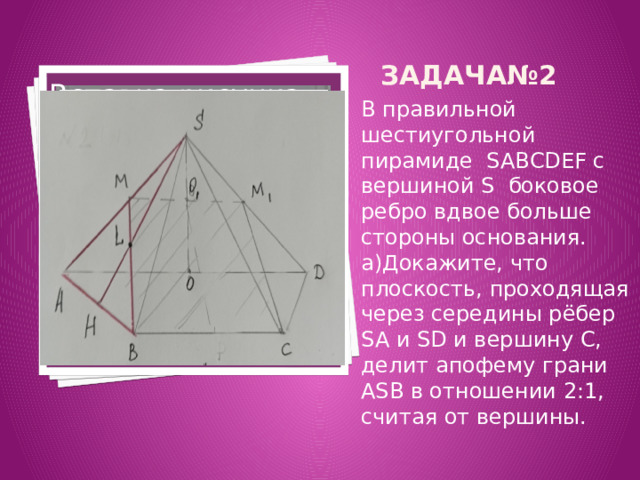
В правильной шестиугольной пирамиде SABCDEF с вершиной S боковое ребро вдвое больше стороны основания.

а)Докажите, что плоскость, проходящая через середины рёбер SA и SD и вершину C, делит апофему грани ASB в отношении 2:1, считая от вершины.

Задача№2

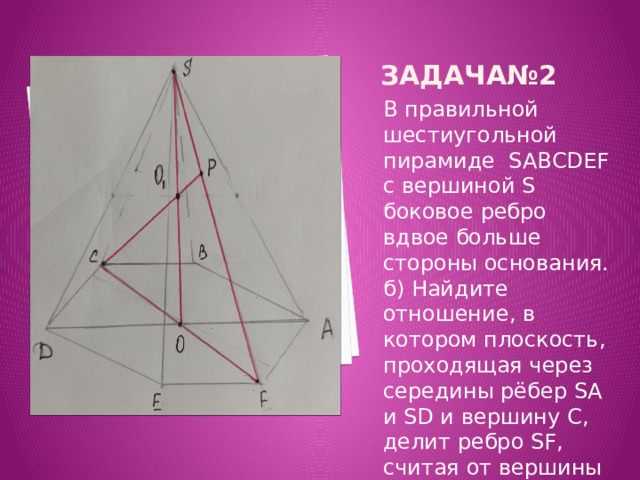
В правильной шестиугольной пирамиде SABCDEF с вершиной S боковое ребро вдвое больше стороны основания.

б) Найдите отношение, в котором плоскость, проходящая через середины рёбер SA и SD и вершину C, делит ребро SF, считая от вершины S.

Координатный метод

• Координатный метод удобно применять, когда требуется:
• Найти угол между прямыми.
• Найти угол между прямой и плоскостью.
• Найти угол между плоскостями.
• Доказать перпендикулярность прямых.
• Доказать перпендикулярность прямой и плоскости.
• Доказать, что точка принадлежит плоскости.
• Найти расстояние от точки до плоскости.
• Найти расстояние между скрещивающимися прямыми.

Алгоритм решения

• Найти угол между прямыми

1) введём прямоугольную декартову систему координат;

2) запишем координаты нужных нам точек во введённой системе координат;

3) найдём координаты направляющих векторов (векторов, лежащих на данных прямых);

4) найдём длины этих векторов и их скалярное произведение;

5) найдём косинус угла между этими векторами – t;

6) найдём α = arccos | t |.

Алгоритмы решения

• Найти расстояние от точки до плоскости

1) введём прямоугольную декартову систему координат;

2) запишем координаты нужных нам точек во введённой системе координат;

3) составим уравнение плоскости, проходящей через три точки:

Ax + By + Cz + D = 0 ( если плоскость не проходит через начало координат, то d=1, если же проходит, то d=0) ;

4) найдем искомое расстояние по формуле:

• Найти расстояние между скрещивающимися прямыми

1) зафиксируем одну прямую;

2) возьмём произвольную точку на второй прямой прямой и проведём через неё прямую , параллельную зафиксированной;

3) через вторую прямую и прямую, параллельную зафиксированной, проведём плоскость α;

4) расстояние между скрещивающимися прямыми будет равно расстоянию от точки, лежащей на первой прямой до плоскости, содержащей вторую прямую.

5) применить предыдущий алгоритм.

Задача №3

• Основание пирамиды SABC-равносторонний треугольник ABC. Боковое ребро SA перпендикулярно плоскости основания, точки М и N — середины рёбер BC и AB соответственно, причём SN=AM

а) Докажите, что угол между прямыми AM и SN равен 60°.

б) Найдите расстояние между этими прямыми, если BC=6.

Алгоритмы решения

• Доказать, что точка принадлежит плоскости

1) введём прямоугольную декартову систему координат;

2) запишем координаты нужных нам точек во введённой системе координат;

3) составим уравнение плоскости, проходящей через три точки:

Ax + By + Cz + D = 0 ( если плоскость не проходит через начало координат, то d=1, если же проходит, то d=0) ;

4) подставим координаты заданной точки в уравнение плоскости.

5) если получится верное равенство, точка принадлежит плоскости.

• Найти расстояние от точки до плоскости

1) введём прямоугольную декартову систему координат;

2) запишем координаты нужных нам точек во введённой системе координат;

3) составим уравнение плоскости, проходящей через три точки:

• Ax + By + Cz + D = 0 ( если плоскость не проходит через начало координат, то d=1, если же проходит, то d=0) ;

4) найдем искомое расстояние по формуле нахождения расстояния от точки до плоскости.

Задача №4

• В правильной треугольной призме ABCA1B1C1 на рёбрах AC и BC отмечены соответственно точки M и N так, что AM:MC=CN:BN=2:1,точка K - середина ребра A1C1.

а) Докажите, что плоскость MNK проходит через вершину B1.

б) Найдите расстояние от точки C до плоскости KMN, если AB=6, AA1=2 ,4