Презентация к внеурочному занятию: "Иоганн Кеплер"

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа № 33

И оганн К еплер

Составила Мамбеталиева Т. В.

г. Ногинск, 2016г.

Цель:

ознакомить с жизнью и научными исследованиями

немецкого ученого Иоганна Кеплера, дать общие понятия о телах вращения и правильных многоугольниках.

Задачи:

Развивать у школьников интерес к познанию окружающего мира.

Иоганн Кеплер   (1571-1630) — немецкий астроном, один из творцов астрономии нового времени. Открыл законы движения планет (законы Кеплера), на основе которых составил планетные таблицы. Заложил основы теории затмений. Изобрел телескоп, в котором объектив и окуляр — двояковыпуклые линзы .

Иоганн Кеплер родился 27 декабря 1571 года в Германии.

Кеплер учился в университете Тюбингена и изучал теологию , философию , математику и астрономию .

В 1596 году Кеплер опубликовал Космографическую Тайну. В этой работе он защищал теории Коперника , который отстаивал позицию о том, что Солнце находится в центре Солнечной Системы.

Иоганн Кеплер полагал, что Вселенная управляется геометрическими отношениями , которые соответствуют вписанной и описанной окружностей пяти регулярных многоугольников .

Три закона Иоганна Кеплера движения планет

Каждая планета Солнечной системы вращается по эллипсу , Солнце находится в одном из фокусов такой планеты;

Каждая планета движется в плоскости , которая проходит через центр Солнца , а за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади .

Квадраты периодов обращения планет вокруг Солнца соотносятся, как кубы больших полуосей орбит планет.

В геометрии Кеплер сделал открытия, подвинувшие ее много вперед. Он выработал понятия и методы, которыми разрешались многие задачи, неразрешимые до него. Кеплер нашёл способ определения объёмов разнообразных тел вращения, который описал в книге «Новая стереометрия винных бочек» (1615).

Тело, происходящее от вращения полукруга вокруг диаметра, называется  шаром , а поверхность, образуемая при этом полуокружностью, называется  шаровой  или  

сферической  поверхностью.

Всякое сечение шара плоскостью

есть круг.

Прямой круговой конус  – это тело, которое получено вращением прямоугольного треугольника вокруг его катета как оси.

Сечение конуса плоскостью, который проходит через вершину конуса – это равнобедренный треугольник. 

Плоскость, которая параллельна основанию конуса и которая пересекает конус, отсекает от него конус меньшего размера.

Оставшаяся часть является  усеченным конусом .

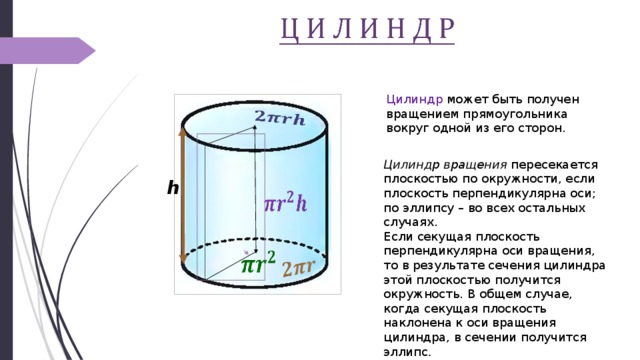
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон .

Цилиндр вращения  пересекается плоскостью по окружности, если плоскость перпендикулярна оси; по эллипсу – во всех остальных случаях.

Если секущая плоскость перпендикулярна оси вращения, то в результате сечения цилиндра этой плоскостью получится окружность. В общем случае, когда секущая плоскость наклонена к оси вращения цилиндра, в сечении получится эллипс .

h

Кроме того, Кеплер очень подробно проанализировал симметрию снежинок . Исследования по симметрии привели его к предположениям о плотной упаковке шаров , согласно которым наибольшая плотность упаковки достигается при пирамидальном упорядочивании шаров друг над другом. Математически доказать этот факт не удавалось на протяжении 400 лет — первое сообщение о доказательстве гипотезы Кеплера появилось лишь в 1998 году

Вклад Кеплера в теорию многогранника

Восстановление математического содержания утерянного трактата Архимеда о полуправильных выпуклых однородных многогранниках.

Предложение рассматривать невыпуклые многогранники со звездчатыми гранями, подобными пентаграмме

Открытие двух правильных невыпуклых однородных многогранников - малого звездчатого додекаэдра и большого звездчатого додекаэдр

Существует 5 видов правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр .

ТЕТРАЭДР

К У Б

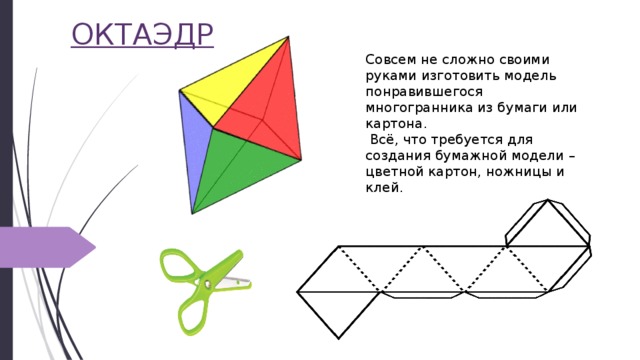
ОКТАЭДР

Совсем не сложно своими руками изготовить модель понравившегося многогранника из бумаги или картона.

Всё, что требуется для создания бумажной модели – цветной картон, ножницы и клей.

ДОДЕКАЭДР

Открытия Иоганна Кеплера внесли неоценимый вклад в развитие астрономии, физики и математики. Некоторые его гипотезы были со временем отвергнуты, а некоторые стали фундаментом для последующих открытий.

Домашнее задание

Собрать из бумаги многоугольник.

СПАСИБО ЗА

ВНИМАНИЕ!

Список использованных при составлении презентации источников

• https://ru.wikipedia.org/wiki/Кеплер,_Иоганн ;
• http://www.vologda.kp.ru/daily/26159.4/3046881/ ;
• http://www.peoples.ru/science/agriculture/iohann_kepler/index1.html
• http://fineartamerica.com

• http://www.vseprokosmos.ru
• http://polyhedron2008.narod.ru/pages/polyhedr.htm
• http://zvzd3d.ru/FromBumaga.html

26 октября 2016г.

Внеклассное мероприятие

«Иоганн Кеплер»

было проведено

в 10 «А» классе.