Презентация на тему: Коды с исправлением и обнаружением ошибок

Проверка четности. Контрольная сумма. Блочные и древовидные коды. Вес и расстояние Хэмминга между двоичными словами.

Коды делятся на два больших класса

Коды с исправлением ошибок  

Цель восстановить с вероятностью, близкой к единице, посланное сообщение.

Коды с обнаружением ошибок  

Цель выявить с вероятностью, близкой к единице, наличие ошибок.

Коды с обнаружением ошибок в передаче

Введение в передаваемые кодовые комбинации избыточных разрядов все множество кодовых комбинаций разбивает на два подмножества, что снижает мощность и информационную скорость кода, но позволяет, при принятой запрещенной кодовой комбинации, обнаружить ошибку в передаче.

Например,

введение дополнительного бита контроля по четности делает четным число единиц в каждой кодовой комбинации равнодоступного кода и одновременно увеличивает их отличия не менее чем до двух разрядов.

Разрешенные кодовые комбинации

Запрещенные кодовые комбинации

Коды с обнаружением ошибок в передаче

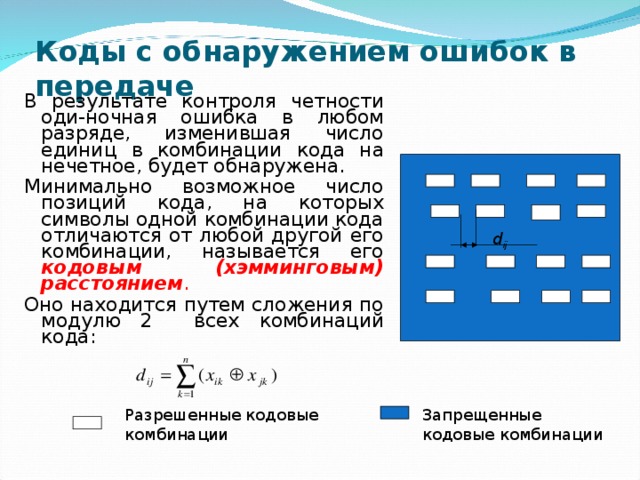
В результате контроля четности оди-ночная ошибка в любом разряде, изменившая число единиц в комбинации кода на нечетное, будет обнаружена.

Минимально возможное число позиций кода, на которых символы одной комбинации кода отличаются от любой другой его комбинации, называется его кодовым (хэмминговым) расстоянием .

Оно находится путем сложения по модулю 2 всех комбинаций кода:

d ij

Разрешенные кодовые комбинации

Запрещенные кодовые комбинации

Виды корректирующих кодов

Коды с исправлением ошибок в передаче

Коды, которые позволяют не только обнаружить ошибку, но и определить номер искаженного символа (позиции), называются кодами с исправлением ошибок .

Для исправления одиночной ошибки придется увеличить кодовое расстояние минимум до 3, двухкратной до 4 и т. п.

В блоковых (блочных) кодах входная непрерывная последовательность информационных символов разбивается на блоки, содержащие k сим - волов.

k . Этот набор, называемый кодовым словом , передается по каналу связи, искажается шумами и помехами, а затем декодируется независимо от всех других кодовых слов. Величина n называется длиной канального кода или длиной канального блока . Каждое сообщение в этом случае передаётся собственным кодовым словом. Кодовые слова могут объединяться в группы – кодовые предложения или фразы, объединённые некоторой общностью, например, способом защиты от помех кодовых слов, входящих в блок, и т. п. " width="640"

Все дальнейшие операции в кодере производятся над каждым блоком отдельно и независимо от других блоков.

Каждому информационному блоку из k символов ставится в соответствие набор из n символов кода канала передачи сообщений, где n k . Этот набор, называемый кодовым словом , передается по каналу связи, искажается шумами и помехами, а затем декодируется независимо от всех других кодовых слов.

Величина n называется длиной канального кода или длиной канального блока . Каждое сообщение в этом случае передаётся собственным кодовым словом.

Кодовые слова могут объединяться в группы – кодовые предложения или фразы, объединённые некоторой общностью, например, способом защиты от помех кодовых слов, входящих в блок, и т. п.

К онтрольная сумма - это некоторое значение, вычисленное по определённой схеме на основе кодируемого сообщения.

Проверочная информация при  систематическом кодировании  приписывается к передаваемым данным.

На принимающей стороне абонент знает алгоритм вычисления контрольной суммы: соответственно, программа имеет возможность проверить корректность принятых данных.

Без контрольной суммы, передавать данные опасно, так как помехи присутствуют везде и всегда, весь вопрос только в их вероятности возникновения и вызываемых ими побочных эффектах.

В зависимости от условий и выбирается алгоритм выявления ошибок и количество данных в контрольной сумме.

Чем сложнее алгоритм, и больше контрольная сумма, тем меньше не распознанных ошибок.

Все алгебраические коды можно разделить на два больших класса:

Блочные (блоковые)

Непрерывные

(древовидные)

Блочные коды представляют собой совокупность кодовых символов, состоящих из отдельных комбинаций (блоков) элементов символов кода, которые кодируются и декодируются независимо. 

Непрерывные (древовидные) коды представляют собой непрерывную последовательность кодовых символов, причем введение проверочных элементов производится непрерывно, без разделения ее на независимые блоки.

В древовидных (непрерывных) кодах информационная последовательность подвергается обработке без предварительного разбиения на независимые блоки. Длинной, полубесконечной информационной последовательности ставится в соответствие кодовая последовательность, состоящая из большего числа символов.

Непрерывными эти коды называются потому, что операции кодирования и декодирования в них совершаются непрерывно. Они способны исправлять пакетные ошибки при сравнительно простых алгоритмах кодирования и декодирования .

Свойства кодов с исправлением ошибок в передаче

Кодированный цифровой сигнал приобретает свойства обнаружения, а иногда и исправления ошибок, возникающих в процессе передачи и приёма сообщений, т. е. свойство помехозащищенности .

Применение специальных криптографических кодов, известных только соответствующим абонентам, обеспечивает секретность передачи, а зашифрованное сообщение приобретает свойство криптографической стойкости .

Первыми появились блоковые коды, они же также лучше теоретически исследованы. Из древовидных кодов проще всего с точки зрения реализации свёрточные и цепные коды .

Возможности блоковых и древовидных кодов по исправлению ошибок передачи примерно одинаковы. Наибольшее распространение в существующих системах передачи получили разделимые систематические коды , а из них – коды Хэмминга и циклические коды.

Расстоя́ние и вес Хэ́мминга

Пусть  u =( u 1 ,  u 2 ,  … ,  u n ) – двоичная последовательность длиной  n .

Число единиц в этой последовательности называется   весом Хэмминга   вектор а   u   и обозначается как   w(u).

Например:  u =( 1 0 0 1 0 1 1 ), тогда  w ( u )= 4 .

Пусть  u   и   v  – двоичные слова длиной   n .

Число разрядов, в которых эти слова различаются, называется   расстоянием Хэмминга   между  u  и  v и обозначается как   d(u, v) .

Например:  u =( 1 0 0 1 0 1 1 ),  v =( 0 1 0 0 0 1 1 ), тогда  d ( u ,  v )= 3 .

Самостоятельно

Найти вес и кодовое расстояние для двоичных слов

• a=011011100
• b=100111001

Решение:  Вес для двоичных слов  w(a)=5    ;  w(b)=  5 .

Кодовое расстояние d(A,B) = 6.