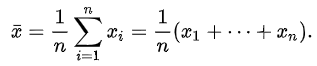| 
| Муниципальное бюджетное общеобразовательное учреждение «Многопрофильный лицей города Димитровграда Ульяновской области» имени заслуженного учителя школы РСФСР Ривгата Рашитовича Ибрагимова |
ИССЛЕДОВАТЕЛЬСКИЙ ПРОЕКТ
Использование математических методов для оценки
экологического состояния окружающей среды
Выполнил:
Киселев А. А.
ученик 9 В класса
Научный руководитель
Кожухарь Е.Д.
учитель математики
Димитровград, 2025 год.
Содержание
Введение 3
Глава 1. Математические и биологические методы, используемые для оценки экологического состояния окружающей среды. 5
1.1. Метод биоиндикации. 5
1.2. Метод флуктуирующей асимметрии. 6
1.3. Математические методы. 8
1.3.1. Понятие симметрии. 8
1.3.2. Среднее арифметическое. 10
Глава 2. Оценка состояния окружающей среды. 13
2.1.Методика проведения эксперимента. 13
2.2. Обработка и оформление результатов измерений. 14
Заключение. 18
Список используемой литературы 19
Приложение 20
Введение
Для жизни человеку нужны чистый воздух, качественная вода, незараженная почва, но с развитием цивилизации вредное воздействие людей на природу становится угрожающим для нее. Во всём мире растёт понимание того, что, разрушая природные системы Земли, человечество уничтожает своё будущее. Однако без изменения сознания человека все планы спасения природной среды останутся лишь благими пожеланиями. Школьники имеют слабое представление об экологическом состоянии окружающей среды, но каждому грамотному человеку необходимо знать, в каких экологических условиях он учится, работает, живёт и отдыхает. Поэтому, я считаю, одной из важных задач в школе является формирование экологического сознания. Это не только любовь и бережное отношение ко всему живому, но и чувство личной ответственности за то, что происходит вокруг, потребность действовать.
Экология - наука о взаимоотношениях между живыми организмами и средой их обитания. Она исследует факторы неживой природы, воздействующие на организмы, а также влияние живых организмов на природу в целом.
Математика наука о структурах, порядке и отношениях, которая исторически сложилась на основе операций подсчёта, измерения и описания форм реальных объектов.
Математика всегда была неотъемлемой и существенной составной частью человеческой культуры, она является ключом к познанию окружающего мира, базой научно-технического прогресса и важным компонентом развития личности. Не зря греческие ученые говорили, что математика есть ключ ко всем наукам.
Применение математических формул, обработка статистических данных помогает экологам решать задачи по восстановлению экологического равновесия в природе. С помощью основ математики мы можем считать и строить диаграммы, проводить точные измерения, делать расчёты и подтверждать наблюдения, а также проводить оценку экологического состояния окружающей среды.
Димитровград – небольшой город, но несмотря на это проблемы экологии, по результатам опроса учеников школы, являются актуальными (Приложение 1).
Не имея возможности проводить комплексные исследования, требующие больших материальных затрат и специального оборудования, для оценки экологического состояния нашего города, мы можем использовать метод биоиндикации, признанный многими учёными.
Целью данной работы является оценка экологического состояния окружающей среды города Димитровграда с помощью математических методов.
Для достижения цели были поставлены следующие задачи:
изучить математическую теорию, связанную с такими понятиями как:
- симметрия
- понятие среднего арифметического
2. изучить метод биоиндикации
3. провести расчеты
4. сделать вывод о состоянии окружающей среды
Методы исследования: работа с учебной и научно-популярной литературой, ресурсами сети Интернет; анализ; математические расчеты; сопоставление полученных данных.
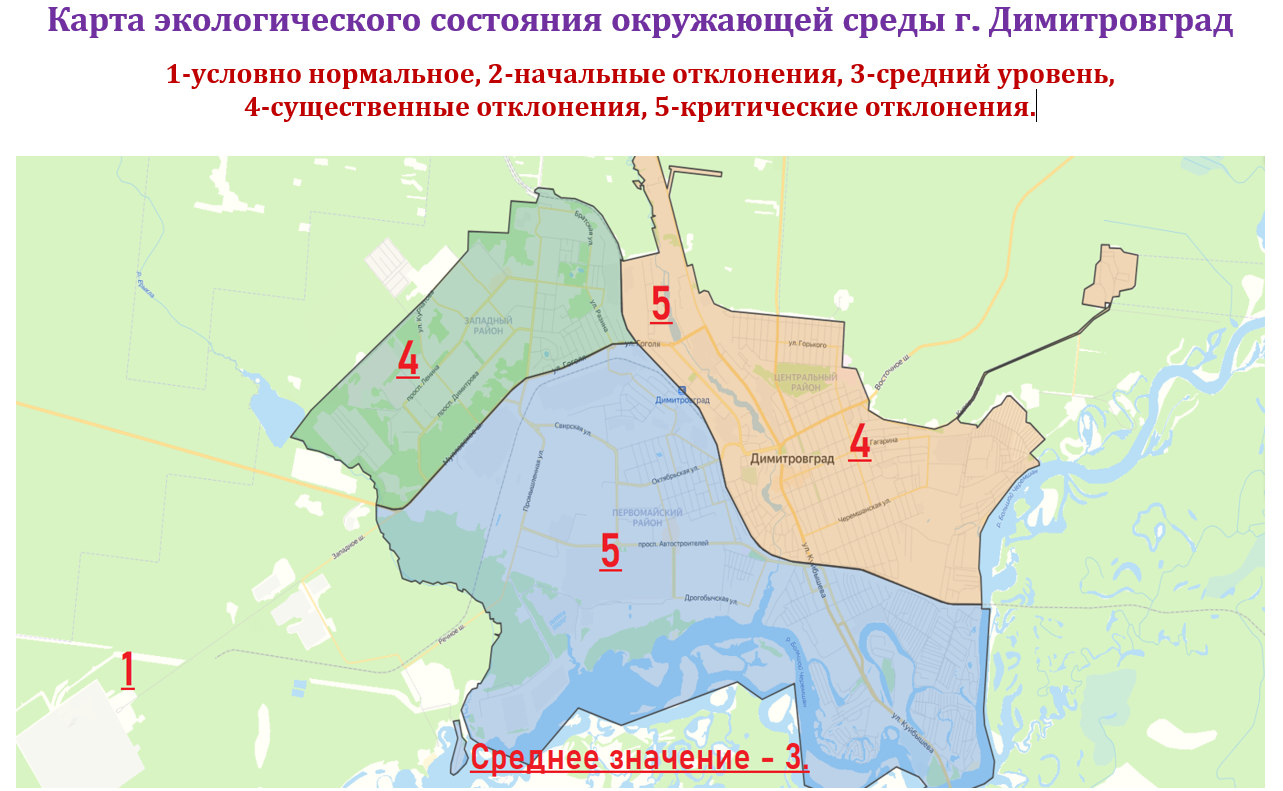
Продукт исследования: карта города с обозначением зон по экологическому состоянию окружающей среды.
Глава 1. Математические и биологические методы, используемые для оценки экологического состояния окружающей среды.
Метод биоиндикации.
В своей работе для оценки экологического состояния окружающей среды я использовал метод биондикации.
Биоиндикация — оценка качества природной среды по состоянию её биоты. Биоиндикация основана на наблюдении за составом и численностью видов-индикаторов.
В ходе онтогенетического и филогенетического развития любой организм в отношении любого фактора обладает генетически детерминированным и филогенетически приобретённым, уникальным физиологическим диапазоном толерантности, в пределах которого данный фактор не оказывает существенного влияния на жизнедеятельность организма, являясь переносимым. В случае низкой или высокой интенсивности силы фактора организм находится в зонах физиологического пессимума, когда силы воздействия находится за максимальными или минимальными пределами для конкретного организма — наступает угнетение жизнедеятельности организма и организм погибает. Данный диапазон неодинаков как для различных особей популяции (но колеблется в пределах определённых для вида) и неодинаков в разные стадии жизненного цикла организма, а также в случае когда значение интенсивности других факторов находятся либо в зоне пессимума или угнетения.
Развитие организма происходит под комплексным, синергетическим воздействием всевозможных комбинаций факторов среды биотической и абиотической природы. Зачастую развитие ограничивают факторы, находящиеся в зоне пессимума или угнетения (так называемое расширенное правило Либиха). В природе происходит лишь частичная реализация физиологических потенциалов — так называемая реализованная экологическая ниша (постконкурентная экологическая ниша, популяционная экологическая ниша, экологический диапазон присутствия, экологический потенциал). Экологический потенциал отражает реакцию организма на воздействие факторов. Физиологическая толерантность и экологическая потенция определяют его индикаторную ценность.
В результате как состояние организма, так и его численность, структура популяции отражают благоприятность состояния окружающей среды. Такие организмы, жизненные функции которых тесно скоррелированны с отдельными факторами среды, называются биоиндикаторами.
Существует две формы биоиндикации: когда одинаковые реакции организма могут быть вызваны различными факторами среды (в том числе и антропогенного происхождения) — тогда речь идёт о неспецифической биоиндикации; когда изменения реакции чётко связаны с изменением конкретного фактора — специфическая биоиндикация.
Метод флуктуирующей асимметрии.
Живые организмы очень чувствительны к изменениям в окружающей их среде. Некоторые из живых организмов служат удобными для человека индикаторами состояния среды. Чтобы живой организм был хорошим биоиндикатором. У него должны проявляться достаточно выразительно ответы на изменения в окружающей среде. Одним из таких выразительных ответов оказалось нарушение симметрии в строении некоторых организмов и их частей.
Отечественные и зарубежные ученые исследовали, насколько строго соблюдают разные организмы симметричность признаков с левой и правой стороны и обнаружили, что при ухудшении состояния среды все чаще возникают сбои в точном соответствии лево- и правосторонних признаков. Был предложен способ учета различия в признаках слева и справа, по результатам которого можно оценить качество природной среды обитания исследуемого организма.
Для исследования подходят признаки, которые можно аккуратно измерить и сравнить между собой. Лучше использовать для одного и того же организма несколько признаков. Чтобы удобнее было сравнивать между собой оценки для разных признаков, величину асимметрии следует учитывать в относительных величинах: учитывать не просто разницу в промерах слева и справа, а относительную величину, которая получается, если разницу в промерах слева и справа разделить на сумму этих промеров. Для учета нужно использовать выборку, состоящую не менее чем из нескольких десятков организмов, и окончательные выводы делать по средним арифметическим значениям. Статистическую значимость различий между выборками по величине показателей стабильности развития определяют по t-критерию Стьюдента.
Для определенного вида организмов ученые оценили величину ассиметрии признаков в условиях, близких к идеальным: например, в лаборатории, где подобраны все наилучшие условия для жизни, или в природе, но там, где нет никаких явных следов вредных воздействий. Эти данные ученые приняли за первый балл. Затем получили результаты в условиях с явно неблагоприятными воздействиями для жизни. Эти данные приняли за пятый балл. Вот, к примеру, как будет выглядеть такая пятибалльная шкала:
| Стабильность развития (в баллах) | Качество среды |
| I | Условно нормальное |
| II | Начальные (незначительные) отклонения от нормы |
| III | Средний уровень отклонений от нормы |
| IV | Существенные (значительные) отклонения от нормы |
| V | Критическое состояние |
Такие балльные системы оценок разработаны к настоящему времени для ряда видов растений, рыб, земноводных и млекопитающих. Этот подход оказался полезным на практике – для фонового мониторинга (в естественных условиях) и для оценки последствий антропогенных воздействий. В связи с этим Министерство природных ресурсов Российской федерации рекомендовало широко использовать этот метод для проведении оценки качества среды, ее благоприятности для человека в целом ряде ситуаций. А именно, для:
определения состояния природных ресурсов;
разработки стратегии рационального использования региона;
выявления зон экологического бедствия;
проведения работ по оценке воздействия на окружающую среду и при перепрофилировании предприятий;
оценки эффективности природоохранных мероприятий;
создания особо охраняемых природных территорий.
В документе, рекомендованном Министерством, приведены списки растений и животных, с помощью которых можно проводить оценки качества среды во всех географических зонах на территории России, за исключением зоны тундр, полупустынь, пустынь и высокогорья.
Математические методы.
Понятие симметрии.
Одним из ключевых критериев метода биоиндикации является симметрия живых организмов.
Симметрия (лат. symmetria, греч. συμμετρία — соразмерность) — особое свойство объектов или явлений, которое характеризуется тем, что они могут быть разделены на части, симметричные относительно некоторой оси, плоскости или центра. В природе существует несколько видов симметрии, каждый из которых имеет свои особенности. Во всех её формах она выражает гармонию и равновесие. В природе сочетание симметрии и асимметрии образует неповторимое и разнообразное множество форм и узоров.
Симметрия является одним из основных понятий геометрии, которое имеет широкое применение в различных областях. Она определена как свойство фигур, при котором части объекта или сам объект отражаются относительно определённой оси, плоскости или центра. Это свойство исследуется и применяется в геометрии, искусстве, архитектуре, физике и многих других областях.
Осевая симметрия
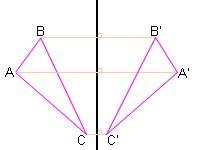
Рисунок 1. Осевая симметрия
Осевая симметрия возникает, когда фигура разделяется на две равные и зеркально отражающиеся части относительно оси. Это обычный вид симметрии, который можно часто наблюдать в природе. Такие объекты, как лица людей, обладают осевой симметрией.
Зеркальная симметрия
Зеркальная симметрия или отражение (симметрия относительно плоскости) — это движение в евклидовом пространстве, при котором множество точек, оставшихся неподвижными, образует гиперплоскость (в трёхмерном пространстве просто плоскость). Термин «зеркальная симметрия» также используется для описания типа симметрии объекта, когда объект при отражении отображается в самого себя. Зеркальная симметрия проявляется во многих законах природы, включая кристаллографию, химию, физику, биологию и другие науки, а также в искусстве и искусствоведении.
Центральная симметрия

Рисунок 2. Центральная симметрия.
Центральная симметрия (симметрия относительно точки) происходит, когда фигура отражается относительно центральной точки. Этот вид симметрии часто встречается в геометрии, особенно в круговых и сферических фигурах. При центральной симметрии относительно точки О, фигура Ф совпадает с самой собой после последовательных отражений от трёх взаимно перпендикулярных плоскостей. Другими словами, точка О является серединой отрезка, соединяющего симметричные точки Ф.
Среднее арифметическое.
Для проведения расчетов необходимо использовать понятие среднего арифметического.
Среднее арифметическое (в математике и статистике) — разновидность среднего значения. Определяется как число, равное сумме всех чисел множества, делённой на их количество. Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки). На случай, если количество элементов множества чисел стационарного случайного процесса бесконечное, в качестве среднего арифметического выступает математическое ожидание случайной величины.
Обозначим множество чисел X = (x1, x2, …, xn) — тогда выборочное среднее обычно обозначается горизонтальной чертой
Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее, или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.
На практике разница между средним арифметическим и выборочным средним в том, что среднее арифметческое является типичной переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда выборочное среднее можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).
Обе эти величины вычисляются одним и тем же способом:
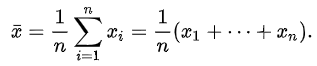
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n+1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины (например, среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное).
Примеры
Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:
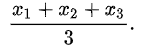
Для получения среднего арифметического четырёх чисел необходимо сложить их и разделить на 4:
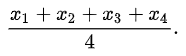
Глава 2. Оценка состояния окружающей среды.
2.1.Методика проведения эксперимента.
Для оценки качества среды я использовал древесное растение – березу повислую (латинское название Betula pendula Roth). Важно с помощью определителя точно установить вид растения и собирать листья именно с березы повислой.
Для проведения исследования выбрал деревья, растущие на открытых участках, так как даже небольшая затененность может вызвать у березы нарушения стабильности развития.
Сбор материала следует проводить после остановки роста листьев (в средней полосе – начиная с июля). В эксперименте использовали листья с нижней части кроны и примерно одинакового, среднего размера.
Измерения проводили с внутренней стороны образца. У каждого листа измерил по четыре признака справа и слева, как показано на рисунке 3.
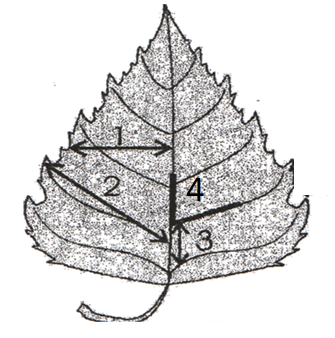
Рисунок 3. Схема морфологических признаков, использованных для оценки стабильности развития березы повислой (Betula pendula).
1 – ширина левой и правой половинок листа. Для измерения лист складывают пополам, совмещая верхушку с основанием листовой пластинки. Потом разгибают лист и по образовавшейся складке измеряется расстояние от границы центральной жилки до края листа;
2 - длина жилки второго порядка, второй от основания листа;
3 – расстояние между основаниями первой и второй жилок второго порядка;
4 – угол между главной жилкой и второй от основания листа жилкой второго порядка.
Промеры проводил с помощью линейки и транспортира. С каждого района города собрал по 6 образцов и провел измерения.
2.2. Обработка и оформление результатов измерений. Для мерных признаков величина асимметрии у растений рассчитывается как различие в промерах слева и справа, отнесенное к сумме промеров на двух сторонах (Таблица 1).
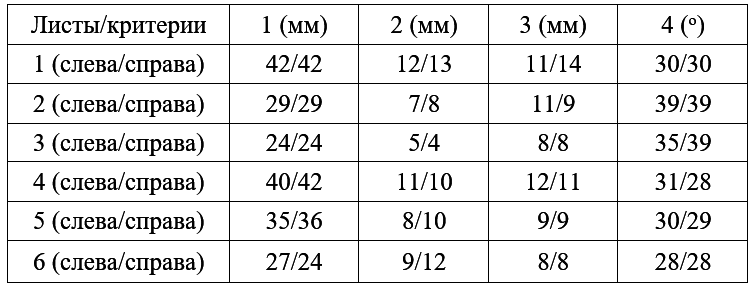
Таблица 1. Промеры образцов Центральный район «Химмаш»
Интегральным показателем стабильности развития для комплекса мерных признаков является средняя величина относительного различия между сторонами на признак. Этот показатель рассчитывается как среднее арифметическое суммы относительной величины асимметрии по всем признакам у каждой особи, отнесенное к числу используемых признаков. Такая схема обработки используется для растений.
Для каждого промеренного листа вычислил относительные величины асимметрии для каждого признака. Для этого модуль разности между промерами слева (л) и справа (п) поделил на сумму этих же промеров:
Yi = ǀ(xп-xл)ǀ : (xп+xл)
Затем вычислил показатель асимметрии для каждого листа, для этого определил сумму значений относительных величин асимметрии по каждому признаку и поделил на число признаков (Таблица 2).
Z = (Y1 + Y2 + Y3 + Y4) : 4
| 1 лист | 2 лист |
| Y1= (42-42) : (42+42) = 0 Y2= (13-12) : (13+12) = 0,04 Y3= (14-11) : (14+11) = 0,12 Y4= (30-30) : (30+30) = 0 Z = (0 + 0,04 + 0,12 + 0) : 4 = 0,04 | Y1= (29-29) : (29+29) = 0 Y2= (8-7) : (8+7) = 0,0(6) Y3= (9-11) : (9+11) = 0,1 Y4= (39-39) : (39+39) = 0 Z = (0 + 0,0(6) + 0,1 + 0) : 4 = 0,041(6) |
Таблица 2. Пример расчета показателя асимметрии (Центральный район Химмаш)
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| Y1 | 0 | 0 | 0 | 0 | 0,01 | 0,06 |
| Y2 | 0,04 | 0,07 | 0,11 | 0,05 | 0,11 | 0,14 |
| Y3 | 0,12 | 0,10 | 0 | 0,04 | 0 | 0 |
| Y4 | 0 | 0 | 0,55 | 0,05 | 0,02 | 0 |
| Z | 0,04 | 0,04 | 0,04 | 0,04 | 0,35 | 0,02 |
| Zср | 0,09 |
На последнем этапе вычислил интегральный показатель стабильности развития – величина среднего относительного различия между сторонами на признак. Для этого вычислил среднюю арифметическую всех величин асимметрии для каждого листа (Таблица 3).
Таблица 3. Среднее значение показателя асимметрии (Центральный район Химмаш)
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| Y1 | 0,04 | 0,04 | 0,07 | 0 | 0 | 0,02 |
| Y2 | 0 | 0 | 0,08 | 0 | 0,11 | 0,14 |
| Y3 | 0,05 | 0,13 | 0,04 | 0 | 0,10 | 0,14 |
| Y4 | 0,06 | 0 | 0,04 | 0,01 | 0,11 | 0,02 |
| Z | 0,04 | 0,04 | 0,06 | 0 | 0,08 | 0,08 |
| Zср | 0,05 |
Аналогичные промеры образцов (Приложение 2) и расчет среднего показателя асимметрии (Таблицы 4,5,6,7) были проведены также для других районов города, включая район Научно-исследовательского института атомных реакторов (НИИАР).
Таблица 4. Среднее значение показателя асимметрии (район НИИАР)
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| Y1 | 0 | 0,01 | 0,1 | 0 | 0 | 0,01 |
| Y2 | 0,10 | 0,14 | 0,10 | 0,25 | 0,10 | 0,14 |
| Y3 | 0,04 | 0,05 | 0,13 | 0,04 | 0,05 | 0,09 |
| Y4 | 0,01 | 0 | 0,06 | 0,04 | 0,01 | 0,04 |
| Z | 0,14 | 0,20 | 0,10 | 0,08 | 0,04 | 0,07 |
| Zср | 0,10 |
Таблица 5. Среднее значение показателя асимметрии (Первомайский район)
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| Y1 | 0,04 | 0 | 0 | 0 | 0,01 | 0 |
| Y2 | 0,06 | 0,09 | 0 | 0 | 0,2 | 0,078 |
| Y3 | 0,07 | 0 | 0,05 | 0,05 | 0 | 0,04 |
| Y4 | 0,08 | 0,11 | 0,05 | 0,06 | 0,03 | 0,02 |
| Z | 0,07 | 0,05 | 0,02 | 0,03 | 0,24 | 0,03 |
| Z ср | 0,07 |
Таблица 6. Среднее значение показателя асимметрии (Западный район)
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| Y1 | 0 | 0,05 | 0,02 | 0,03 | 0 | 0,05 |
| Y2 | 0 | 0,11 | 0,11 | 0 | 0 | 0 |
| Y3 | 0,06 | 0,44 | 0,13 | 0,10 | 0,06 | 0,05 |
| Y4 | 0,44 | 0 | 0,01 | 0 | 0,03 | 0,01 |
| Z | 0,12 | 0,15 | 0,07 | 0,03 | 0,02 | 0,03 |
| Zср | 0,07 |
Таблица 7. Среднее значение асимметрии (Центральный район «Старый город»)
Статистическая значимость различий между выборками по величине интегрального показателя стабильности развития (величина среднего относительного различия между сторонами на признак) определяется по t-критерию Стьюдента.
Для оценки степени выявленных отклонений листьев березы от нормы, их места в общем диапазоне возможных изменений показателя разработана балльная шкала. Диапазон значений интегрального показателя асимметрии, соответствующий условно нормальному фоновому состоянию, принимается как первый балл (условная норма). Он соответствует данным, полученным в природных популяциях при отсутствии видимых неблагоприятных воздействий (например, на особо охраняемых природных территориях). В этой связи надо иметь в виду, что на практике при оценке среды в регионе с повышенной антропогенной нагрузкой фоновый уровень нарушений в выборке растений или животных даже из точки условного контроля не всегда находится в диапазоне значений, соответствующих первому баллу. Диапазон значений, соответствующий критическому состоянию, принимается за пятый балл. Он соответствует тем популяциям, где есть явное неблагоприятное воздействие и такие изменения состояния организма, которые приводят организм к гибели. Весь диапазон между этими пороговыми уровнями ранжируется в порядке возрастания значений показателя.
Пятибалльная шкала оценки отклонений состояния организма от условий нормы по величине интегрального показателя стабильности развития для березы повислой (Betula pendula) (Таблица 8):
| Балл | Величина показателя стабильности развития |
| I |
|
| II | 0,056 - 0,060 |
| III | 0,061 – 0,065 |
| IV | 0,066 – 0,070 |
| V | 0,071 |
Таблица 8. Шкала оценки отклонений состояния организма от условий нормы для березы повислой (Betula pendula)
В соответствии со шкалой оценки и данными измерений представлены результаты оценки состояния окружающей среды города Димитровграда. (Таблица 9).
| Район города | Среднее значение асимметрии, zср | Балл |
| Центральный район «Химмаш» | 0,09 | V |
| Центральный район «Старый город» | 0,07 | IV |
| Первомайский район | 0,10 | V |
| Западный район | 0,07 | IV |
| НИИАР | 0,05 | I |
| Среднее значение | 0,06 | III |
Таблица 9. Оценка экологического состояния окружающей среды г. Димитровграда.
Заключение.
В результате проведенных исследований, мы пришли к выводу, что деревья очень чувствительны к изменениям окружающей среды, и в первую очередь это проявляется в строении их листьев. С помощью метода биоиндикации и методов математического анализа можно оценить экологическое состояние окружающей среды. Цель нашей работы была достигнута.
На основании результатов нашего исследования была составлена карта города Димитровграда с обозначением баллов, указывающих на качество среды (Приложение 3). В отдельных районах города он указывает на существенные или критические отклонения от нормы. В среднем показатель по городу и близлежащей территории говорит, о среднем уровне отклонения показателя от нормы.
Можно сделать вывод, что экологическое состояния нашего города не является идеальным и далеко от нормы. Изменение в отрицательную сторону качества среды обитания оказывает влияние на растения, на животных и на человека, что подчеркивает актуальность и важность проекта.
Н.Н. Моисеев – российский ученый в области механики и прикладной математики, говорил: «Человечество должно научиться жить в согласии с Природой, с её законами. Люди должны воспринимать себя не господами, а частью Природы». Я считаю, что нам, подрастающему поколению нужно больше изучать проблемы экологии, и использовать для этого различные методы, в том числе математические.
Список используемой литературы
Биондикация в городах и пригородных зонах / Под ред. Д.А. Криволуцкого. – М.: Наука, 1993.
Биоиндикация загрязнений наземных экосистем / Под ред. Р. Шуберта. – М.: Мир.
Васильев А.Г., Большакова В.Н. Взгляд на эволюционную экологию вчера и сегодня / А.Г. Васильев, В.Н, Большакова // Экология. 1994, № 8.
Губанов И.А., Киселева К.В., Новиков В.С., Тихомиров В.И. Определитель сосудистых растений центра европейской России. – М.: Аргус, 1995.
Захаров В.М. Здоровье среды: методика оценки. – М.: Центр экологической политики России, 2001.
Лукин Ю.Н. Анализ техногенного воздействия на экосистемы региона: учеб. пособие. – М.: Диалог, 1998.
Труды второй международной научно-практической конференции молодых ученых «Индикация состояния окружающей среды: теория, практика, образование», 25-28 апреля 2013 года: сборник статей. – М.: ООО «Буки Веди», 2013.
Экологический практикум школьника / С.В. Алексеев, Н.В. Груздева, Э.В Гущина, Издательство «Учебная литература», 2005.
Геометрия, 7-9Учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др., Издательство «Просвещение, АО «Московские учебники», 2001.
Приложение Приложение 1.
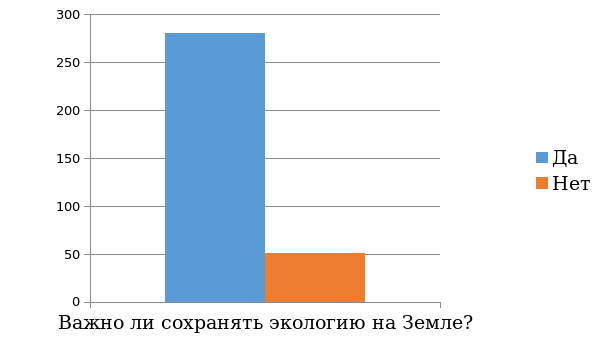
Для выявления мнения об экологическом состоянии Димитровграда мной был проведен опрос среди X школьников. Им были заданы следующие вопросы и представленные варианты ответа:
Важно ли сохранять экологи на Земле и почему?
Да
Нет
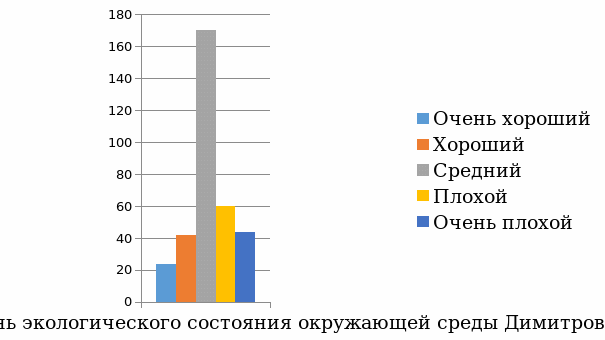
Как вы оцениваете уровень экологического состояния окружающей среды Димитровграда?
Очень хороший
Хороший
Средний
Плохой
Очень плохой
По результатам опроса я составил следующие диаграммы:
Приложение 2.
| Листы/критерии | 1 (мм) | 2 (мм) | 3 (мм) | 4 (о) |
| 1 (слева/справа) | 36/39 | 5/5 | 10/11 | 40/45 |
| 2 (слева/справа) | 36/39 | 5/5 | 13/10 | 49/49 |
| 3 (слева/справа) | 32/37 | 6/7 | 12/13 | 40/43 |
| 4 (слева/справа) | 30/30 | 3/3 | 11/11 | 50/51 |
| 5 (слева/справа) | 34/34 | 4/5 | 12/10 | 44/35 |
| 6 (слева/справа) | 33/34 | 4/3 | 9/12 | 50/48 |
Промеры образцов район НИИАР
Промеры образцов Первомайский район
| Листы/критерии | 1 (мм) | 2 (мм) | 3 (мм) | 4 (о) |
| 1 (слева/справа) | 35/38 | 8/7 | 13/15 | 39/33 |
| 2 (слева/справа) | 33/33 | 6/5 | 11/11 | 44/43 |
| 3 (слева/справа) | 35/35 | 5/5 | 11/10 | 40/45 |
| 4 (слева/справа) | 38/38 | 5/5 | 10/11 | 52/46 |
| 5 (слева/справа) | 42/41 | 6/4 | 15/15 | 46/49 |
| 6 (слева/справа) | 35/35 | 7/6 | 14/13 | 40/42 |
| Листы/критерии | 1 (мм) | 2 (мм) | 3 (мм) | 4 (о) |
| 1 (слева/справа) | 41/41 | 5/6 | 12/11 | 41/40 |
| 2 (слева/справа) | 37/36 | 3/4 | 11/10 | 39/39 |
| 3 (слева/справа) | 36/44 | 6/5 | 10/13 | 31/35 |
| 4 (слева/справа) | 37/37 | 5/3 | 11/12 | 42/39 |
| 5 (слева/справа) | 35/35 | 5/6 | 10/9 | 39/38 |
| 6 (слева/справа) | 38/37 | 3/4 | 12/10 | 36/39 |
Промеры образцов Западный район
| Листы/критерии | 1 (мм) | 2 (мм) | 3 (мм) | 4 (о) |
| 1 (слева/справа) | 25/25 | 5/5 | 8/9 | 41/39 |
| 2 (слева/справа) | 30/33 | 4/5 | 11/12 | 48/48 |
| 3 (слева/справа) | 27/26 | 4/5 | 9/7 | 48/49 |
| 4 (слева/справа) | 29/31 | 3/3 | 9/11 | 48/48 |
| 5 (слева/справа) | 26/26 | 2/2 | 9/8 | 52/49 |
| 6 (слева/справа) | 33/30 | 3/3 | 9/10 | 48/47 |
Промеры образцов Центральный район «Старый город»
Приложение 3.