Оглавление
| Введение | 2 |
| 1. Теоретическая часть Треугольник важнейшая и неисчерпаемая фигура в геометрии
| 4 |
| 2. Практическая часть Построения при помощи линейки, имеющей форму равностороннего треугольника
| 7 |
| Заключение
| 10 |
| Используемые источники
| 11 |
Введение
Геометрия является самым могущественным
средством для изощрения наших умственных
способностей и дает нам возможность
правильно мыслить и рассуждать
Галилео Галилей
Среди огромного количества самых разнообразных книг, по геометрии начиная от школьных учебников и кончая олимпиадными сборниками cложно объединить известные или малоизвестные нам свойства геометрических фигур и их элементов. Поэтому появилось желание поглубже и повнимательнее рассмотреть, доказать иногда очевидное, иногда поразительное, а иногда просто фантастические, изумительные свойства привычных нам фигур.
На создание работы натолкнула старинная задача:
Сколько равносторонних треугольников изображено на знаменитой печати царя Соломона, изображенной на его гробнице?

Изучая школьный курс по планиметрии, мы часто сталкиваемся с понятием равностороннего треугольника, знаем его определение, основные свойства, формулы, умеем строить с помощью циркуля и линейки. Родилась идея собрать и неизвестные в школьном курсе задачи на построения при помощи линейки, имеющей форму равностороннего треугольника.
Объект исследования- изучение различных свойств равностороннего треугольника и задач на построение, связанных с ним.
Предмет исследования –подбор задач на построения при помощи линейки, имеющей форму равностороннего треугольника. .
Цель работы – выяснить, какие геометрические преобразования выполняются при помощи линейки, имеющей форму равностороннего треугольника.
Поставленная цель достигается решением следующих задач:
1) сформулировать естественные правила работы с равносторонним треугольником-шаблоном;
2 выполнить построения, необходимые для выполнения геометрических преобразований.
При решении этих задач используются теоретические методы исследования, не выходящие за рамки школьного курса планиметрии.
Гипотеза: правильный треугольник можно разбить на шесть меньших правильных треугольников, необязательно равных и нельзя разбить на два, три и пять меньших правильных треугольников.
Актуальность темы: геометрическая форма треугольника находит различное применение в сферах деятельности человека: в инженерии (металлические фермы мостов – составляющие их балки образуют треугольники), в армии (воинские звания), в медицине, в музыке и т.д.
1 Теоретическая часть
Треугольник важнейшая и неисчерпаемая фигура в геометрии
Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которых человек узнал в глубокой древности, т. к. эта фигура всегда имела широкое применение в практической жизни.
Изображения треугольников и задачи на треугольники встречаются во многих папирусах, которым более 4000 лет, в Древней Греции и Древнего Египта. Древнегреческий ученый Герон (I век) впервые применил знак ∆ вместо слова треугольник.. В древнем искусстве очень широко распространяются изображения равностороннего треугольника. Первобытные люди штамповали треугольники на разных изделиях. Вожди племен североамериканских индейцев носили на груди символ власти: равносторонний треугольник с точкой в центре, в Африке женщины также украшают себя большими пластинами из равносторонних треугольников. Равносторонние треугольники рисовали - на изображениях священных животных.
Уже тогда была известна теорема, получившая впоследствии название теоремы Пифагора, которая применялась для построения прямых углов на местности с помощью веревочного треугольника со сторонами 3, 4, 5 (египетский треугольник). Через 2000 лет в древней Греции учение о треугольнике достигает высокого уровня. Известны такие древнегреческие ученые, как Архимед, Пифагор, Фалес.
Учение о треугольнике развивалось в ионийской школе, основанной в VII веке до нашей эры Фалесом, затем в школе Пифагора. Древние греки решили упорядочить накопленные сведения о треугольнике и написали много трудов. Наиболее совершенной оказалась работа Евклида "Начала" (365-300 до н.э.).
Треугольник - простейшая плоская фигура: три вершины и три стороны. Но с древнейших времен и до наших дней математики занимаются изучением треугольника.
Можно сделать вывод: треугольник важнейшая и неисчерпаемая фигура в геометрии.
Основные свойства равностороннего треугольника
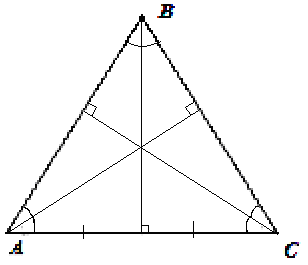
Определение 1. Если все три стороны треугольника равны, то такой треугольник называется равносторонним.
Он является частным видом равнобедренного треугольника.
Свойство 1. Высота равностороннего треугольника, опущенная на строну, одновременно является биссектрисой угла между сторонами, медианой и осью симметрии стороны.
Свойство 2. В равностороннем треугольнике совпадают все замечательные точки: центр тяжести, центры вписанной и описанной окружностей, точка пересечения высот (называемая ортоцентром треугольника).
Свойство 3. Из всех треугольников с заданным периметром равносторонний треугольник имеет наибольшую площадь.
Свойство 4. Из всех треугольников с заданной площадью равносторонний треугольник имеет наименьший периметр
Третий признак равенства треугольников.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Из третьего признака равенства треугольников следует, что треугольник - жёсткая фигура. Поясним, что это означает. Представим себе две рейки, у которых два конца скреплены гвоздем. Такая конструкция не является жёсткой: сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними. Теперь возьмем ещё одну рейку и скрепим её концы со свободными концами первых двух реек. Полученная конструкция - треугольник - будет уже жёсткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему признаку равенства треугольников.
Рассмотрим модели двух фигур - треугольника и четырёхугольника и выясним, можно ли, не меняя длины сторон, изменить форму фигуры? Под действием небольшой силы четырёхугольник изменил свою форму, а треугольник нет.
Вывод: можно сказать, что треугольник – не изменяющаяся фигура. В нем нельзя сдвинуть или раздвинуть никакие две стороны, в отличие от любого другого многоугольника. В треугольнике нельзя изменить ни один из углов. Таким образом, треугольник – жесткая фигура.
2 Практическая часть
Построения при помощи линейки, имеющей форму равностороннего треугольника
Существуют задачи на построения, выполняемые при помощи линейки, имеющей форму равностороннего треугольника.
1. Пользуясь односторонней линейкой и шаблоном имеющим форму правильного треугольника, разделите данный отрезок на 2 равных отрезка.

С помощью линейки продолжим отрезок АВ за точки А и В, затем с помощью шаблона по разные стороны прямой АВ построим два равносторонних треугольника. Отрезок, соединяющих вершины этих треугольников, пересекает отрезок АВ в его середине.
2. Пользуясь односторонней линейкой и шаблоном, имеющим форму правильного треугольника, разделите данный отрезок на три равных отрезка.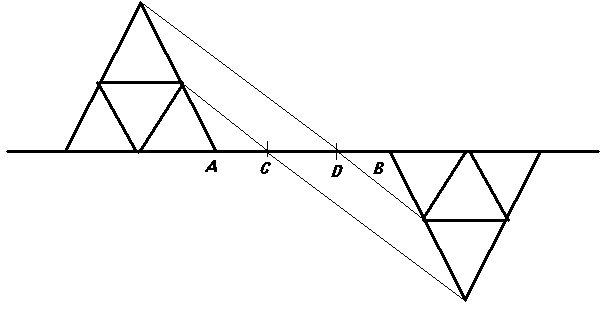
Выполнив построения, показанные на рисунке, получим точки C и D, делящие отрезок АВ на три равные части.
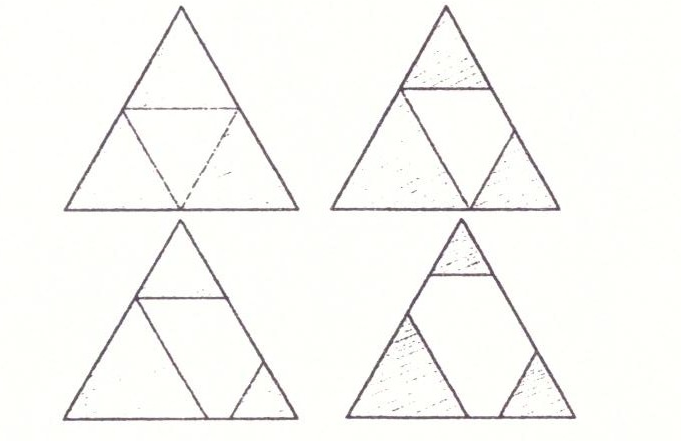
3. Правильный треугольник можно ли разбить на шесть меньших правильных треугольников, необязательно равных, и на два, три и пять меньших правильных треугольников.
Разбить правильный треугольник на 6 меньших правильных треугольников можно. Это хорошо видно на чертеже.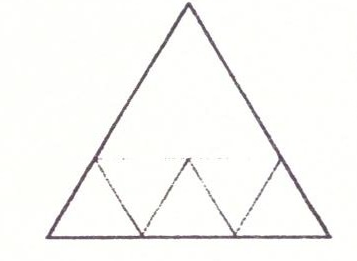

Покажем, что правильный треугольник нельзя разбить на два, три и пять меньших правильных треугольников. Каждая вершина правильного треугольника является вершиной одного из треугольников разбиения. Причем ни один треугольник разбиения не может содержать двух вершин основного треугольника. Поэтому правильный треугольник нельзя разбить на два меньших правильных треугольника.
Правильный треугольник нельзя разбить и на три меньших треугольника, так как два меньших треугольника должны содержать по одной вершине основного треугольника. А фигура, которая получится, если из основного удалить два малых правильных треугольника, расположенных в его углах, не будет треугольником: она может быть либо четырехугольником (точнее параллелограммом), либо пятиугольником.
Аналогично, поскольку фигура, которая получится, если из основного треугольника удалить три малых правильных треугольника, расположенных в его углах, не может быть разбита на два правильных треугольника.
Итак, правильный треугольник нельзя также разбить и на пять меньших правильных треугольников.
Заключение
Значение геометрии непрерывно возрастает. В геометрии возрождаются новые идеи и методы, всё это расширяет сферу и её приложения. Сейчас уже нельзя назвать такой области, деятельности людей, где геометрия не играла бы существенной роли. Даже юристы и историки берут на своё вооружение геометрические методы. В жизни на каждом шагу мы встречаемся с геометрическими телами. В нашем проекте представлены лишь азы начала геометрии. Работа над проектом существенно поменяла наше отношение к выполнению домашних заданий, мы не боимся совершать ошибки при решении задач и знаем, что любую задачу можно решить различными способами.
Цель работы – выяснить, какие геометрические преобразования выполняются при помощи линейки, имеющей форму равностороннего треугольника - достигнута.
Нами были сформулированы естественные правила работы с равносторонним треугольником-шаблоном;
выполнены построения, необходимые для выполнения геометрических преобразований.
При решении этих задач были использованы теоретические методы исследования, не выходящие за рамки школьного курса планиметрии.
Гипотеза подтвердилась: правильный треугольник можно разбить на шесть меньших правильных треугольников, необязательно равных, и нельзя разбить на два, три и пять меньших правильных треугольников.
Используемые источники:
1. http://math.ru/lib/92
2. http://mirknig.com/knigi/nauka_ucheba
3. http://hijos.ru/2012/10/24/teorema-napoleona/
5
Тема: «Построения при помощи линейки, имеющей форму равностороннего треугольника»

























