Разработка презентации по геометрии в 7 классе на тему "Прямоугольный треугольник и его свойства".

Прямоугольный треугольник

и его свойства

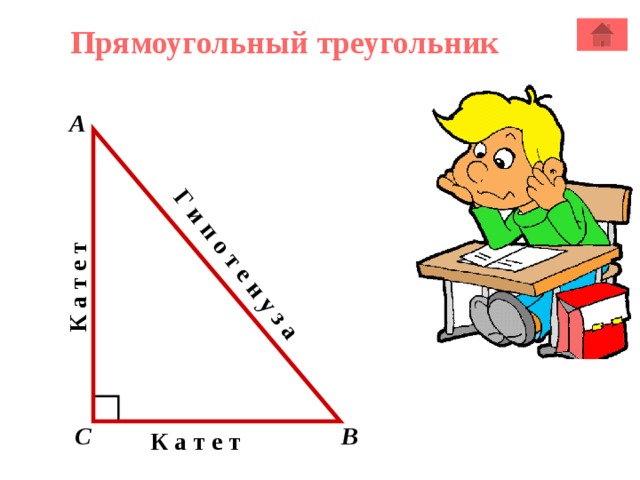
К а т е т

Г и п о т е н у з а

Прямоугольный треугольник

А

В

С

К а т е т

Свойство прямоугольного треугольника.

1

А

В

С

В прямоугольном треугольнике

сумма острых углов равна 90 0 .

Свойство прямоугольного треугольника.

2

А

30 0

В

С

В прямоугольном треугольнике катет, лежащий

против угла в 30 0 , равен половине гипотенузы

Свойство прямоугольного треугольника.

3

А

30 0

В

С

В прямоугольном треугольнике катет, равный

половине гипотенузы лежит против угла в 30 0 .

Свойства прямоугольного треугольника

Сумма двух острых углов прямоугольного треугольника равна 90 0

Катет прямоугольного треугольника, лежащий против угла в 30 0 , равен половине гипотенузы

Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30 0

Признаки равенства

прямоугольных треугольников

• Если катеты одного прямоугольного треугольника

соответственно равны катетам другого, то такие треугольники равны.

Докажем?

2. Если катет и прилежащий к нему острый угол одного прямоугольного

треугольника соответственно равны катету и прилежащему к нему углу

другого, то такие треугольники равны.

Докажем?

3. Если гипотенуза и острый угол одного прямоугольного треугольника

соответственно равны гипотенузе и острому углу другого,

то такие треугольники равны.

Докажем?

4. Если гипотенуза и катет одного прямоугольного треугольника

соответственно равны гипотенузе и катету другого,

то такие треугольники равны.

Докажем ?

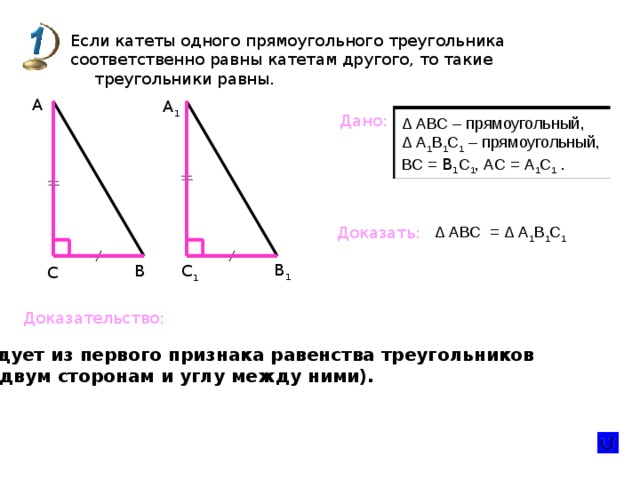
Если катеты одного прямоугольного треугольника

соответственно равны катетам другого, то такие треугольники равны.

А

А 1

Дано:

∆ АВС – прямоугольный,

∆ А 1 В 1 С 1 – прямоугольный,

ВС = В 1 С 1 , АС = А 1 С 1 .

∆ АВС = ∆ А 1 В 1 С 1

Доказать:

В 1

С 1

В

С

Доказательство:

следует из первого признака равенства треугольников

(по двум сторонам и углу между ними).

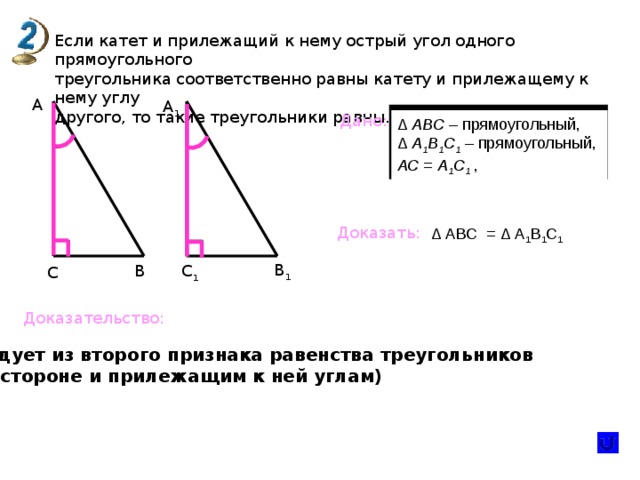
Если катет и прилежащий к нему острый угол одного прямоугольного

треугольника соответственно равны катету и прилежащему к нему углу

другого, то такие треугольники равны.

А

А 1

Дано:

∆ АВС – прямоугольный,

∆ А 1 В 1 С 1 – прямоугольный,

АС = А 1 С 1 ,

Доказать:

∆ АВС = ∆ А 1 В 1 С 1

В 1

С 1

В

С

Доказательство:

следует из второго признака равенства треугольников

(по стороне и прилежащим к ней углам)

9

Если гипотенуза и острый угол одного прямоугольного треугольника

соответственно равны гипотенузе и острому углу другого,

то такие треугольники равны.

А

А 1

Дано:

∆ АВС – прямоугольный,

∆ А 1 В 1 С 1 – прямоугольный,

АВ = А 1 В 1 ,

∆ АВС = ∆ А 1 В 1 С 1

Доказать:

В 1

С 1

В

С

Доказательство:

т.к. сумма острых углов прямоугольного треугольника равна 90 °,

то два других острых угла также равны,

поэтому треугольники равны

по второму признаку равенства треугольников

(по стороне и прилежащим к ней углам).

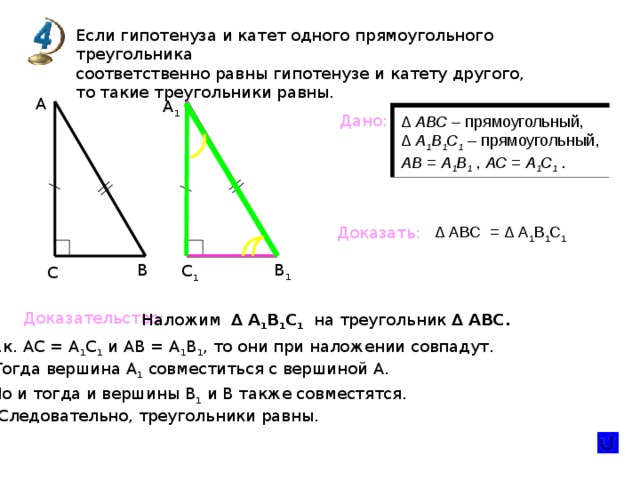
Если гипотенуза и катет одного прямоугольного треугольника

соответственно равны гипотенузе и катету другого,

то такие треугольники равны.

А

А 1

Дано:

∆ АВС – прямоугольный,

∆ А 1 В 1 С 1 – прямоугольный,

АВ = А 1 В 1 , АС = А 1 С 1 .

∆ АВС = ∆ А 1 В 1 С 1

Доказать:

В 1

В

С 1

С

Доказательство:

Наложим ∆ А 1 В 1 С 1 на треугольник ∆ АВС.

Т.к. АС = А 1 С 1 и АВ = А 1 В 1 , то они при наложении совпадут.

Тогда вершина А 1 совместиться с вершиной А.

Но и тогда и вершины В 1 и В также совместятся.

Следовательно, треугольники равны.

Спасибо за внимание!